CPM（Cluster Percolation method）派系过滤算法

本文主要是介绍CPM（Cluster Percolation method）派系过滤算法，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

原文地址

一、概念

（1）完全子图/全耦合网络/k-派系：所有节点全部两两相连

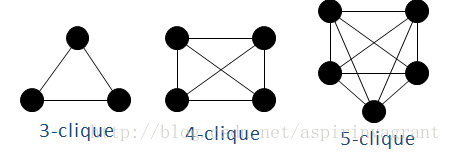
图1

这些全耦合网络也成为派系，k-派系表示该全耦合网络的节点数目为k

1）k-派系相邻：两个不同的k-派系共享k-1个节点，认为他们相邻

2）k-派系连通：一个k-派系可以通过若干个相邻的k-派系到达另一个k-派系，则称这两个k-派系彼此联通

二、思路

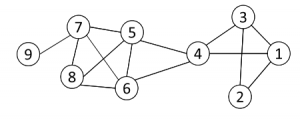
图2

1- first find all cliques of size k in the graph

第一步首先找到网络中大小为K的完全子图，例如图2中k=3的完全子图有{1, 2, 3} {1, 3, 4} {4, 5, 6} {5, 6, 7} {5, 6, 8} {5, 7, 8} {6, 7, 8}
2- then create graph where nodes are cliques of size k

第二步将每个完全子图定义为一个节点，建立一个重叠矩阵

a=[3 2 0 0 0 0 0；

2 3 1 0 0 0 0；

0 1 3 2 2 1 1;

0 0 2 3 2 2 2;

0 0 2 2 3 2 2;

0 0 1 2 2 3 2;

0 0 1 2 2 2 3 ]
3- add edges if two nodes (cliques) share k-1 common nodes

第三步将重叠矩阵变成社团邻接矩阵，其中重叠矩阵中对角线小于k，非对角线小于k-1的元素全置为0

a=[1 1 0 0 0 0 0；

1 1 0 0 0 0 0；

0 0 1 1 1 0 0;

0 0 1 1 1 1 1;

0 0 0 1 1 1 1;

0 0 0 1 1 1 1 ]

4- each connected component is a community

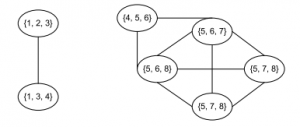
画出派系图，如上所示

从图中可以看出包含了两个社区{1，2，3，4}和{4，5，6，7，8}，节点4属于两个社区的重叠节点

三、代码实现

R实现代码和Java实现代码可在GitHub网站上下载，R下载地址

https://github.com/angelosalatino/CliquePercolationMethod-R

四、References

Palla, G., Derényi, I., Farkas, I., & Vicsek, T. (2005). Uncovering the overlapping community structure of complex networks in nature and society. Nature, 435(7043), 814-818.

注意事项：

CPM算法不适用于稀疏矩阵，K的取值对结果影响不大，一般实验证明4-6为最佳

2017年4.16更新

用matlab算法实现，其中做了一点小变动，k是最小派系范围，寻找的是大于等于k的完全子图数，得到结果与上述描述结果一致，节点4是重叠节点

  function  [components,cliques,CC] = k_clique(k,M) 
 % k-clique algorithm for detecting overlapping communities in a network 
 % as defined in the paper "Uncovering the overlapping 
 % community structure of complex networks in nature and society" - 
 % G. Palla, I. Derényi, I. Farkas, and T. Vicsek - Nature 435, 814–818 (2005) 
 % 
 % [X,Y,Z] = k_clique(k,A) 
 % 
 % Inputs: 
 % k - clique size 
 % A - adjacency matrix 
 % 
 % Outputs: 
 % X - detected communities 
 % Y - all cliques (i.e. complete subgraphs that are not parts of larger 
 % complete subgraphs) 
 % Z - k-clique matrix 
 % 
 % Author : Anh-Dung Nguyen 
 % Email : anh-dung.nguyen@isae.fr 
 % The adjacency matrix of the example network presented in the paper 
 % M = [1 1 0 0 0 0 0 0 0 1; 
 %     1 1 1 1 1 1 1 0 0 1; 
 %     0 1 1 1 0 0 1 0 0 0; 
 %     0 1 1 1 1 1 1 0 0 0; 
 %     0 1 0 1 1 1 1 1 0 0; 
 %     0 1 0 1 1 1 1 1 0 0; 
 %     0 1 1 1 1 1 1 1 1 1; 
 %     0 0 0 0 1 1 1 1 1 1; 
 %     0 0 0 0 0 0 1 1 1 1; 
 %     1 1 0 0 0 0 1 1 1 1]; 
 nb_nodes =  size (M,1);  % number of nodes 
 % Find the largest possible clique size via the degree sequence: 
 % Let {d1,d2,...,dk} be the degree sequence of a graph. The largest 
 % possible clique size of the graph is the maximum value k such that 
 % dk >= k-1 
 degree_sequence =  sort ( sum (M,2) - 1, 'descend' ); 
 max_s = 0; 
 for  i  = 1: length (degree_sequence) 
      if  degree_sequence( i ) >=  i  - 1 
          max_s =  i ; 
      else 
          break ; 
      end 
 end 
 cliques =  cell (0); 
 % Find all s-size kliques in the graph 
 for  s = max_s:-1:3 
      M_aux = M; 
      % Looping over nodes 
      for  n = 1:nb_nodes 
          A = n;  % Set of nodes all linked to each other 
          B =  setdiff ( find (M_aux(n,:)==1),n);  % Set of nodes that are linked to each node in A, but not necessarily to the nodes in B 
          C = transfer_nodes(A,B,s,M_aux);  % Enlarging A by transferring nodes from B 
          if  ~ isempty (C) 
              for  i  =  size (C,1) 
                  cliques = [cliques;{C( i ,:)}]; 
              end 
          end 
          M_aux(n,:) = 0;  % Remove the processed node 
          M_aux(:,n) = 0; 
      end 
 end 
 % Generating the clique-clique overlap matrix 
 CC =  zeros ( length (cliques)); 
 for  c1 = 1: length (cliques) 
      for  c2 = c1: length (cliques) 
          if  c1==c2 
              CC(c1,c2) =  numel (cliques{c1}); 
          else 
              CC(c1,c2) =  numel ( intersect (cliques{c1},cliques{c2})); 
              CC(c2,c1) = CC(c1,c2); 
          end 
      end 
 end 
 % Extracting the k-clique matrix from the clique-clique overlap matrix 
 % Off-diagonal elements <= k-1 --> 0 
 % Diagonal elements <= k --> 0 
 CC( eye ( size (CC))==1) = CC( eye ( size (CC))==1) - k; 
 CC( eye ( size (CC))~=1) = CC( eye ( size (CC))~=1) - k + 1; 
 CC(CC >= 0) = 1; 
 CC(CC < 0) = 0; 
 % Extracting components (or k-clique communities) from the k-clique matrix 
 components = []; 
 for  i  = 1: length (cliques) 
      linked_cliques =  find (CC( i ,:)==1); 
      new_component = []; 
      for  j  = 1: length (linked_cliques) 
          new_component =  union (new_component,cliques{linked_cliques( j )}); 
      end 
      found = false; 
      if  ~ isempty (new_component) 
          for  j  = 1: length (components) 
              if  all ( ismember (new_component,components{ j })) 
                  found = true; 
              end 
          end 
          if  ~found 
              components = [components; {new_component}]; 
          end 
      end 
 end 
      function  R = transfer_nodes(S1,S2,clique_size,C) 
          % Recursive function to transfer nodes from set B to set A (as 
          % defined above) 
           
          % Check if the union of S1 and S2 or S1 is inside an already found larger 
          % clique 
          found_s12 = false; 
          found_s1 = false; 
          for  c = 1: length (cliques) 
              for  cc = 1: size (cliques{c},1) 
                  if  all ( ismember (S1,cliques{c}(cc,:))) 
                      found_s1 = true; 
                  end 
                  if  all ( ismember ( union (S1,S2),cliques{c}(cc,:))) 
                      found_s12 = true; 
                      break ; 
                  end 
              end 
          end 
           
          if  found_s12 || ( length (S1) ~= clique_size &&  isempty (S2)) 
              % If the union of the sets A and B can be included in an 
              % already found (larger) clique, the recursion is stepped back 
              % to check other possibilities 
              R = []; 
          elseif  length (S1) == clique_size; 
              % The size of A reaches s, a new clique is found 
              if  found_s1 
                  R = []; 
              else 
                  R = S1; 
              end 
          else 
              % Check the remaining possible combinations of the neighbors 
              % indices 
              if  isempty ( find (S2>= max (S1),1)) 
                  R = []; 
              else 
                  R = []; 
                  for  w =  find (S2>= max (S1),1): length (S2) 
                      S2_aux = S2; 
                      S1_aux = S1; 
                      S1_aux = [S1_aux S2_aux(w)]; 
                      S2_aux =  setdiff (S2_aux(C(S2(w),S2_aux)==1),S2_aux(w)); 
                      R = [R;transfer_nodes(S1_aux,S2_aux,clique_size,C)]; 
                  end 
              end 
          end 
      end 
 end 
 