本文主要是介绍学习笔记之——2D Gaussian Splatting（2DGS），希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！
3DGS在辐射场重建中取得了巨大的成就，实现高质量的新视图合成和快速渲染。最近新出了3DGS的升级版本，2DGS。写下本博文记录本人学习及测试2DGS的过程，本博文仅为本人学习记录用~
- Project Website
- Github Code
- Original paper
目录
原理解读
什么是surfels?
2DGS与3DGS的区别
2DGS的理解
2DGS 的Modeling
2DGS的Splatting
2DGS的Rasterization
2DGS的训练及loss
Depth Distortion
Normal Consistency
Final Loss
代码测试
代码解读
参考材料
原理解读
由于3D 高斯在多视角下的不一致性，使得它在surface reconstruction中效果不佳。为此，作者提出用2D平面高斯圆盘（2D oriented planar Gaussian disks）来表征三维单元。2DGS通过采用surfels的表达方式，并使用针对surfels的投影方法较好地保证了多视角一致性。通过ray-splat intersection和 rasterization实现2D高斯的渲染。进一步的，通过在loss中引入depth distortion and normal consistency提高了重建几何的质量，而不能单单只靠RGB的loss。
从motivation来看，应该就是3D高斯难以处理复杂的几何形状下的重建，特别是平面会有比较多的noise（这点之前大量的实验也可观察到，也确实3D高斯球叠加一起的平面肯定有些棱角之类的noise）。对于3D高斯而言，对于相邻高斯球交汇处，不同的视角会有不同的渲染值/深度值（3DGS evaluates a Gaussian’s value at the intersection between a pixel ray and a 3D Gaussian, which leads to inconsistency depth when rendered from different viewpoints.）
而采用2D 高斯，也就是类似于Mesh或者surfels差不多的平面来构建的话，可以交换的拟合复杂的平面。
什么是surfels?
Surfels approximate the object surface locally with shape and shade attributes, and can be derived from known geometry.
Surfels（surface elements）是体积渲染文献中的“表面元素”或“表面体素”。其他人将其描述为零维n元组，其形状和阴影属性局部近似于对象表面。对象可以由一组密集的点（表面）表示，这些点（表面）保存照明信息。
A surfel, that is, a point structure representing Euclidean xyz coordinates, together with normal coordinates, a RGBA color, a radius, a confidence value and the surface curvature estimate.
其表达如下：
基于surfels的方法基本上都需要几何的GT、深度信息或者在光照已知的场景下才能运行。而2DGS将其结合起来。2DGS采用了扁平的基元（2D高斯，oriented elliptical disk）对3D场景进行表示，2DGS的基元辐射场垂直于其法线，使其可以更好地贴合场景表面。
2DGS与3DGS的区别
关于3DGS的原理，此处就不再阐述了，请见博客：学习笔记之——3D Gaussian Splatting及其在SLAM与自动驾驶上的应用调研_3d gaussian splatting slam-CSDN博客
虽然3DGS取得巨大的成就，但是由于3D 高斯在多视角下的不一致性，使得它在surface reconstruction中效果不佳。而2D高斯则是多视觉一致性强。而2DGS使用2D的圆盘来表示场景，这使得2DGS与3DGS相比能够表达精确的表面几何。3DGS通过像素发出的光线束和3D Gaussian之间的交平面来计算投影到像平面的高斯值，这在不同视点进行渲染时会导致得到不同的depth（因此depth sort的结果也会不连续）。2DGS使用ray-splat来得到准确连续的投影结果，大大提高了几何的质量。如下图所示。对于3DGS而言，不同的视角，其对应的是不同的交互平面（Intersection Plane），但是对于2DGS，都是相同的平面，因此多视角一致性较强~
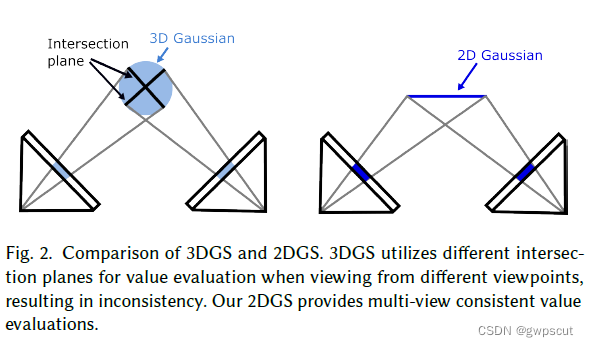
此外，2D高斯中固有的表面法线使得能够通过法线约束进行直接的重构表面进行正则化，因此相比于传统的surfel-based的方法，2DGS可以从未知几何体中恢复。（2DGS天生具有normal使其可以很自然地使用normal进行监督，并且2DGS可以通过基于梯度的优化方法从未知的几何中进行重建。）
如下图所示，2DGS所构建的平面光滑一些~
下图放大一些细节就更明显了~
虽然效果比较不错，但是2DGS是通过不透明度来判断场景的表面，对于诸如玻璃一类半透明的物体会遇到较大困难。其次，2DGS的densification策略使其主要集中在纹理较丰富区域，对于弱纹理区域表示较差。
2DGS的理解
2DGS 的Modeling
2DGS采用了扁平的基元(planar disk)对场景进行表示，2DGS的基元辐射场垂直于其法线(the normal as the direction of steepest change of density)，使其可以更好地贴合场景表面。也有其他类似的工作采用2D 高斯来做几何重建，但是需要稠密的点云以及真值法向量作为输入，但是本文只需要colmap或sfm得到的稀疏点以及作为supervision的图片。
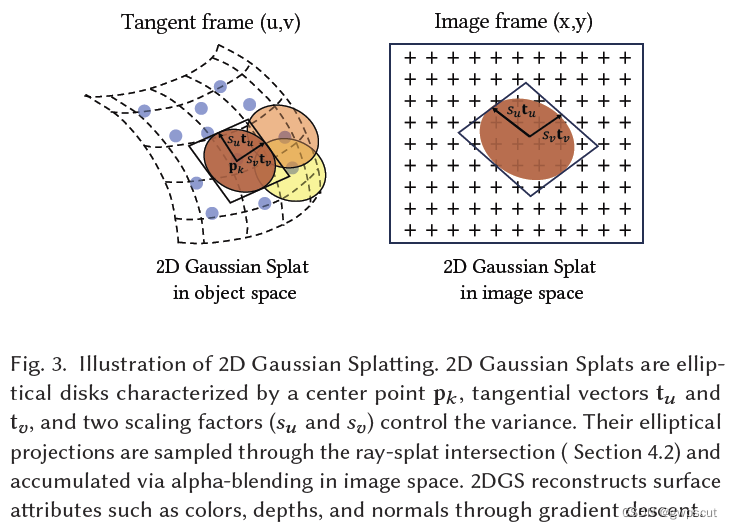
如所图所示。2D高斯的定义为：其中心点 ，两个切向量
和
一个控制2D Gaussians 方差的scaling向量(scalling vector)
。2D Gaussians的法线由两个互相正交的切向量来定义
。因此2D高斯的方位参数可以组织成旋转矩阵
，缩放参数（scalling factors）可以组织为最后一列为0的对角矩阵 𝑆 。
一个2D Gaussian被定义在3D空间中局部的切平面（local tangent plane）坐标系如下：
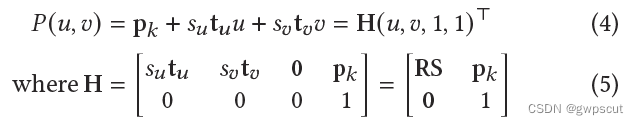
其中H ∈ 4 × 4 是一个齐次变换矩阵，可以表示2D Gaussian的几何形状。这里的点u = (𝑢, 𝑣)是在2D Gaussian的局部的切平面（local tangent plane）中取得的，可以理解为此时高斯函数的均值为0，方差为1，因此可以通过一个简单的公式高效地计算点 𝑢 的函数值：
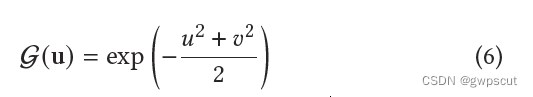
随后可以通过矩阵 𝐻 将局部点 𝑢 变换到全局坐标系中。中心点 、尺度
、rotation
都是可学习的参数，并且与3DGS一样，2D Gaussian基元也有opacity 𝛼 和通过球谐函数计算的视角依赖的外观c。
2DGS的Splatting
渲染2D Gaussians的常用策略是利用透视投影的仿射近似将2D Gaussian基元投影到image space。但这个方法只有在接近基元中心是准确的，离中心越远误差越大。为了解决这个问题，采用基于齐次坐标的计算公式，将2D splat的投影过程描述为齐次表示下一个统一的2D-to-2D的映射。让W ∈ 4 × 4 为world space到camera space到变换矩阵(transformation matrix from world space to screen space)，则screen space到点可以通过下式进行计算：
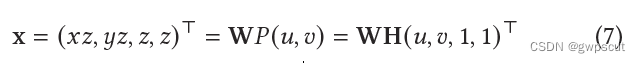
其中 𝑥 表示从像素 (𝑥,𝑦) 发射点一条齐次坐标表示的光线，其与2D splat在深度 𝑧 处相交。因此，给定一个屏幕坐标 (𝑥,𝑦) ，可以计算得到Gaussian space的坐标 
。但这个逆变换矩阵带来了数值的不稳定性，特别是从侧面观察splat退化为线段时。以前的一些方法会设定一个阈值，当splat退化到一定程度时就不再使用这个变换，但这又会使得可微渲染的优化过程不稳定。为了解决这个问题，2DGS使用了一个显式的ray-splat intersection。
Ray-splat Intersection: 2DGS中采用了计算三个非平行平面的交点来得到ray和splat的交点。首先从图像坐标系下任意点 𝑥=(𝑥,𝑦) 出发，根据其两个坐标轴方向的normal (−1,0,0),(0,−1,0) 和任意位移量 𝑥,𝑦 确定两个以齐次坐标表示的平面，这两个平面的交线确定从对应像素发出的ray。接下来将这两个平面变换到2D Gaussian的局部坐标系下（将平面内的点进行变换时使用变换矩阵 𝑀 ,等价于使用其逆转置矩阵
）：
由前面得到的2D Gaussian局部坐标系下点坐标为 (𝑢,𝑣,1,1) ，以及ray-splat intersection位于两个平面内，可以得到：
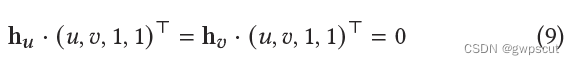
通过这个式子可以导出ray-splat intersection的计算公式：
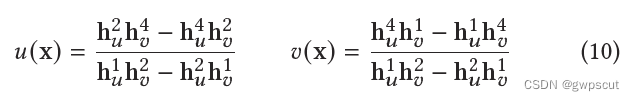
其中分别代表齐次坐标平面的第i个参数。
Degenerate Solutions: 从一些很斜的角度看，2D Gaussian会退化成一条线，在rasterization过程中会突然消失。为了解决这个问题，2DGS中使用一个object-space的低通滤波：
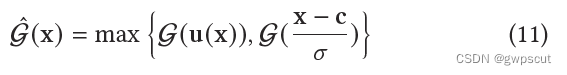
其中 𝑢(𝑥) 为ray-splat intersection， 𝑐 是投影后的2D Gaussian的中心。
2DGS的Rasterization
2DGS的rasterization过程与3DGS一致，首先为2D Gaussian计算一个screen space的bound ing box，然后将2D Gaussians按照其depth进行排序并且根据bounding box将其划分为多个tiles，最后使用volumetric α blending来累加得到最终的color：
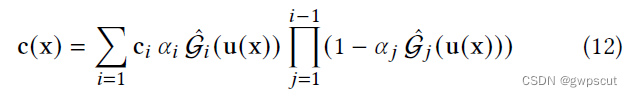
2DGS的训练及loss
如果仅仅使用photometric loss，重建得到的几何会比较noisy，于是2DGS引入了两个regularization terms对几何进行约束。
（由于3D重建任务的多解性，2DGS中除了rgb loss外还使用了两个loss，分别是对depth的监督和对normal连续性的约束。通过额外的两个约束，使得2DGS能够重建出精确的mesh）
Depth Distortion
由于3DGS的体渲染没有考虑intersected高斯基元之间的距离，因此分散的高斯会导致相似的颜色和深度渲染，即体渲染过程中没有准确地对表面部分进行渲染。为了解决这个问题，可以通过最小化ray-splat intersections之间的距离，来使体渲染的权重尽量集中在表面：
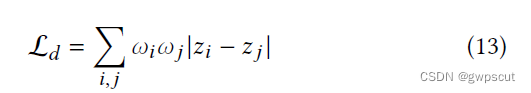
其中，
。2DGS在CUDA中对这一项进行了高效的实现。
Normal Consistency
2DGS这种基于2D Gaussians的surfels表达需要在局部上保证和真实的表面对齐，但体渲染中一条光线上可能会有多个半透明的surfels，于是2DGS将中间的surfels即累积不透明度为0.5的点视为真实表面所在的位置。随后将真实表面位置对应的normal与depth maps的梯度对齐：
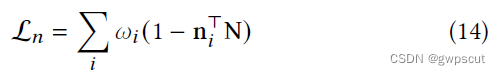
其中 𝑖 代表沿着光线排列的intersected splat， 𝜔 代表交点处的blending weight， 𝑛𝑖 代表splat朝向camera的法线， N 代表depth maps的归一化梯度，可以由下式计算：
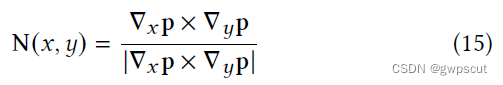
Final Loss
最终的loss为：
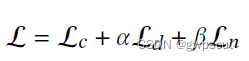
其中第一项为rgb loss， 𝛼=100∼1000,𝛽=0.05。那么就是Normal Consistency的贡献量相对少些？
下面图例将2DGS与3DGS的数学模型放在一起对比，有助于更加直观的感受二者的区别~
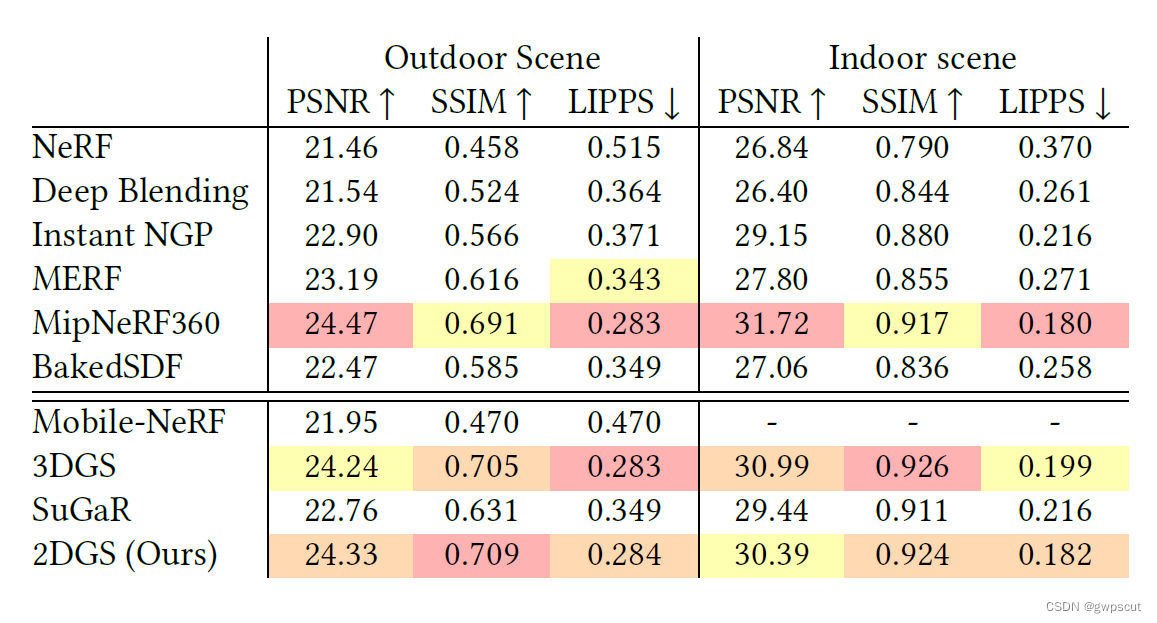
至于从论文的实验来看，视觉效果好像是2DGS好不少，但是数值效果跟3DGS差不多~
代码测试
安装
git clone https://github.com/hbb1/2d-gaussian-splatting.git --recursive# if you have an environment used for 3dgs, use it
# if not, create a new environment
conda env create --file environment.yml
conda activate surfel_splatting由于之前已经有3DGS的环境了，因此直接用原来的conda环境
conda activate 3DGS但是运行的时候会报错，大几率是环境名字不一样，所以不能直接用3DGS的环境，重新安装2DGS的环境~
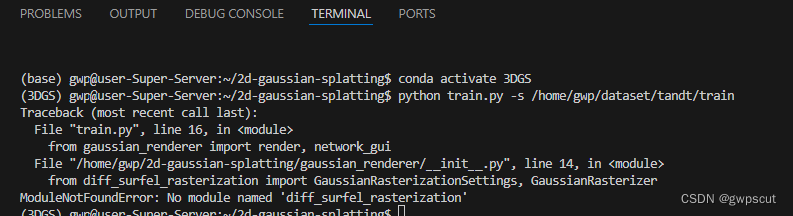
但是还是会报错如下：
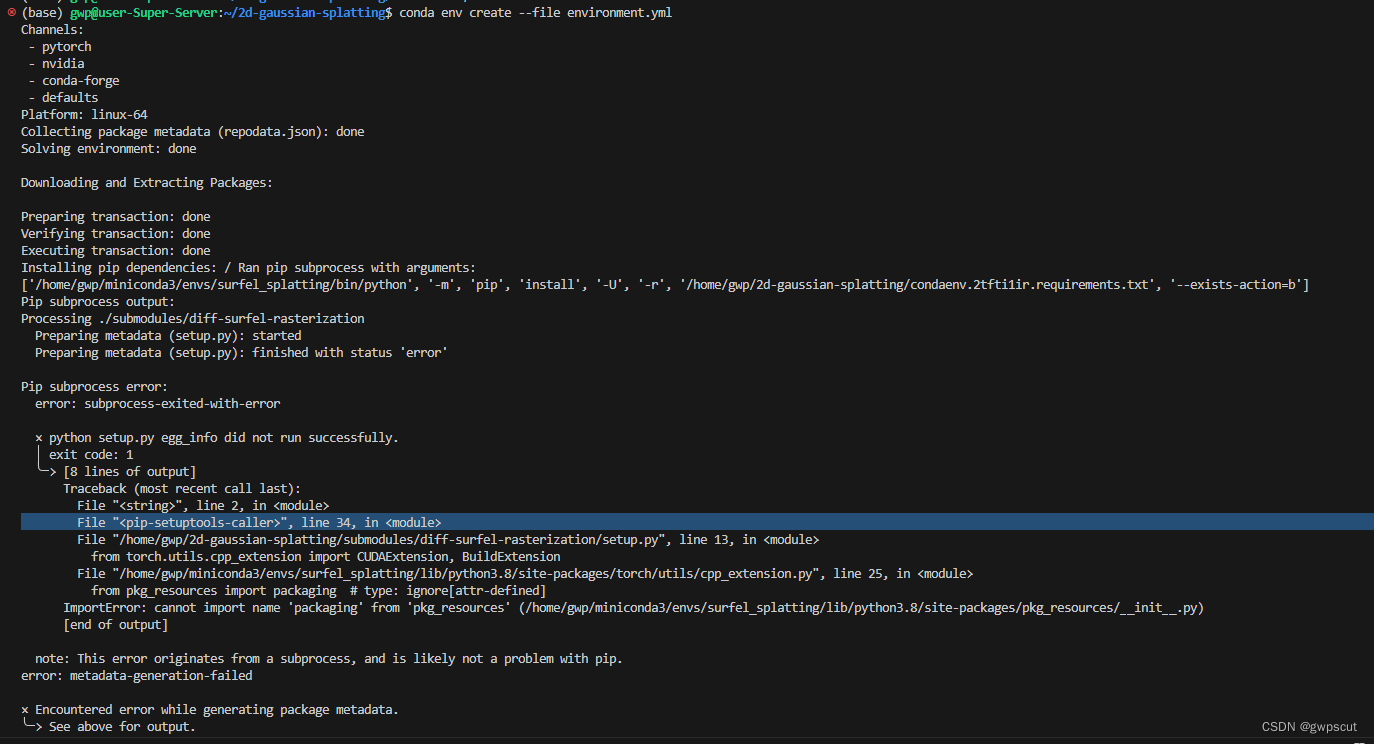
看上去像是setuptools版本有问题。应该是由于安装的python包的环境不对？为此先把构建好的conda 环境remove掉。然后更新一下yaml文件如下
name: surfel_splatting
channels:- pytorch- nvidia- conda-forge- defaults
dependencies:- ffmpeg=4.2.2- pillow=10.2.0- pip=23.3.1- python=3.8.18- pytorch=2.0.0- torchaudio=2.0.0- torchvision=0.15.0- typing_extensions=4.9.0- setuptools=69.5.1- pip:- open3d==0.18.0- mediapy==1.1.2- lpips==0.1.4- scikit-image==0.21.0- tqdm==4.66.2- trimesh==4.3.2- submodules/diff-surfel-rasterization- submodules/simple-knnconda remove --name surfel_splatting --all
conda env create --file environment.yml
conda activate surfel_splatting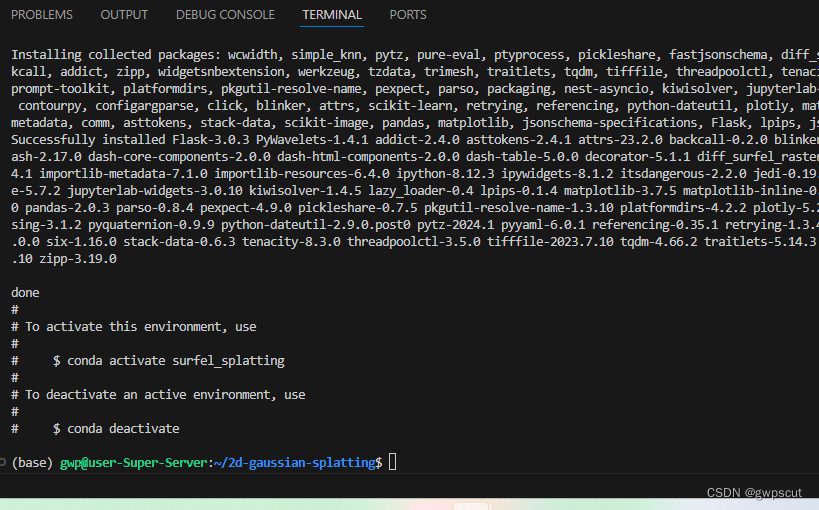
配置成功
开启训练
conda activate surfel_splattingpython train.py -s <path to COLMAP or NeRF Synthetic dataset>#测试tandt数据集
python train.py -s /home/gwp/dataset/tandt/train -m output/tandt/train #验证
python render.py -s /home/gwp/dataset/tandt/train -m output/tandt/train --unbounded --skip_test --skip_train --mesh_res 1024
但是会报错No module named 'plyfile'
pip install plyfile，然后再运行
又显示ModuleNotFoundError: No module named 'cv2'
安装
pip install opencv-python
终于可以了~~~~
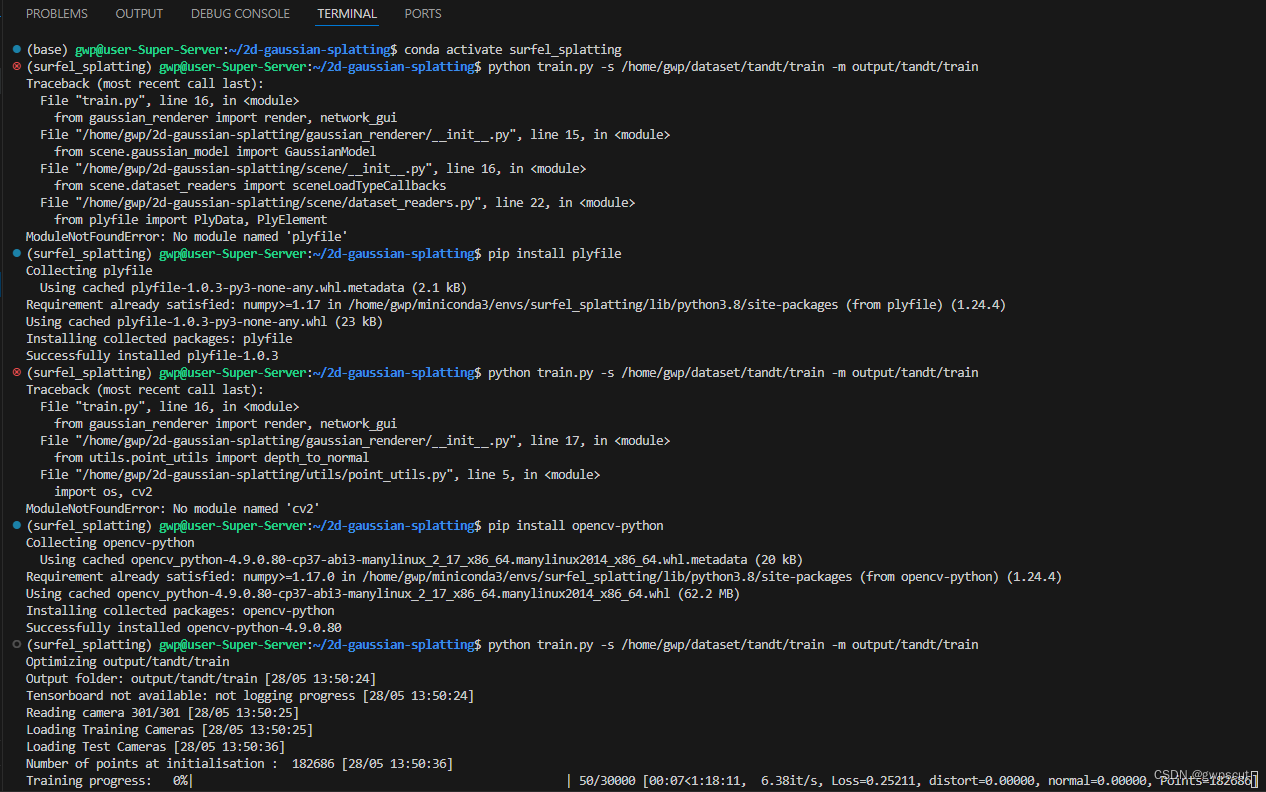
先试试采用MobaXterm用SIBR_remoteGaussian_app来可视化，但是没有任何输出~（github issue中也提出了online SIBR viewer for 2dgs · Issue #17 · hbb1/2d-gaussian-splatting · GitHub）
因此，需要等待有模型保存后再运行下面命令
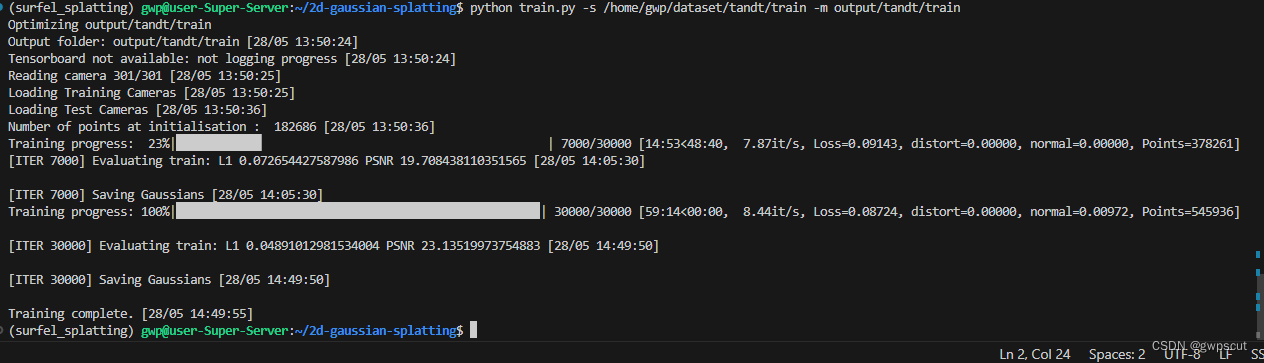
训练完后也有对应的模型输出了~
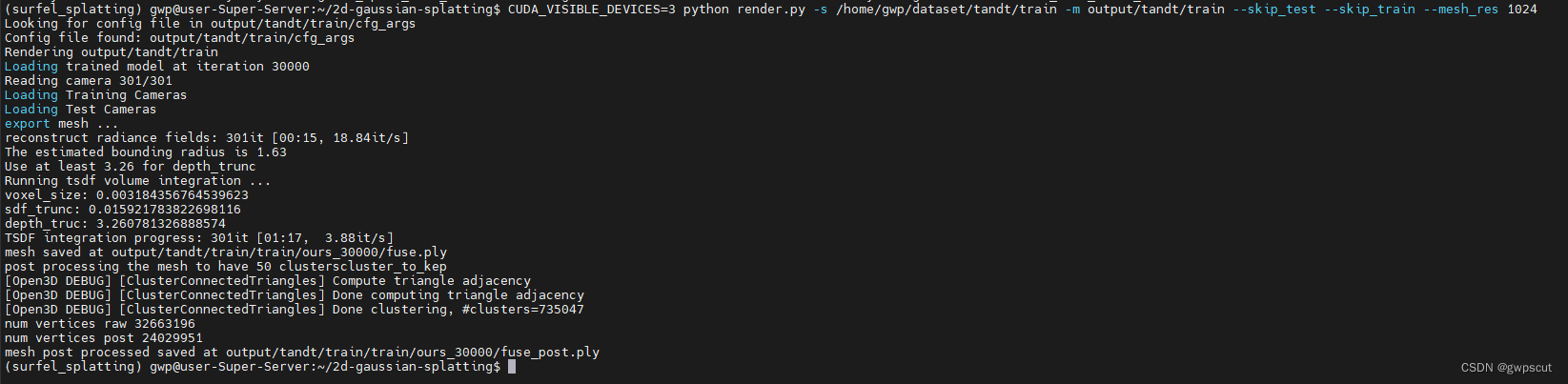
conda activate surfel_splatting#验证
python render.py -s /home/gwp/dataset/tandt/train -m output/tandt/train --unbounded --skip_test --skip_train --mesh_res 1024CUDA_VISIBLE_DEVICES=3 python render.py -s /home/gwp/dataset/tandt/train -m output/tandt/train --unbounded --skip_test --skip_train --mesh_res 1024CUDA_VISIBLE_DEVICES=3 python render.py -s /home/gwp/dataset/tandt/train -m output/tandt/train --skip_test --skip_train --mesh_res 1024注意模型太大可能会爆掉内存，感觉这个可视化还是有点问题~（加载模型也很慢）
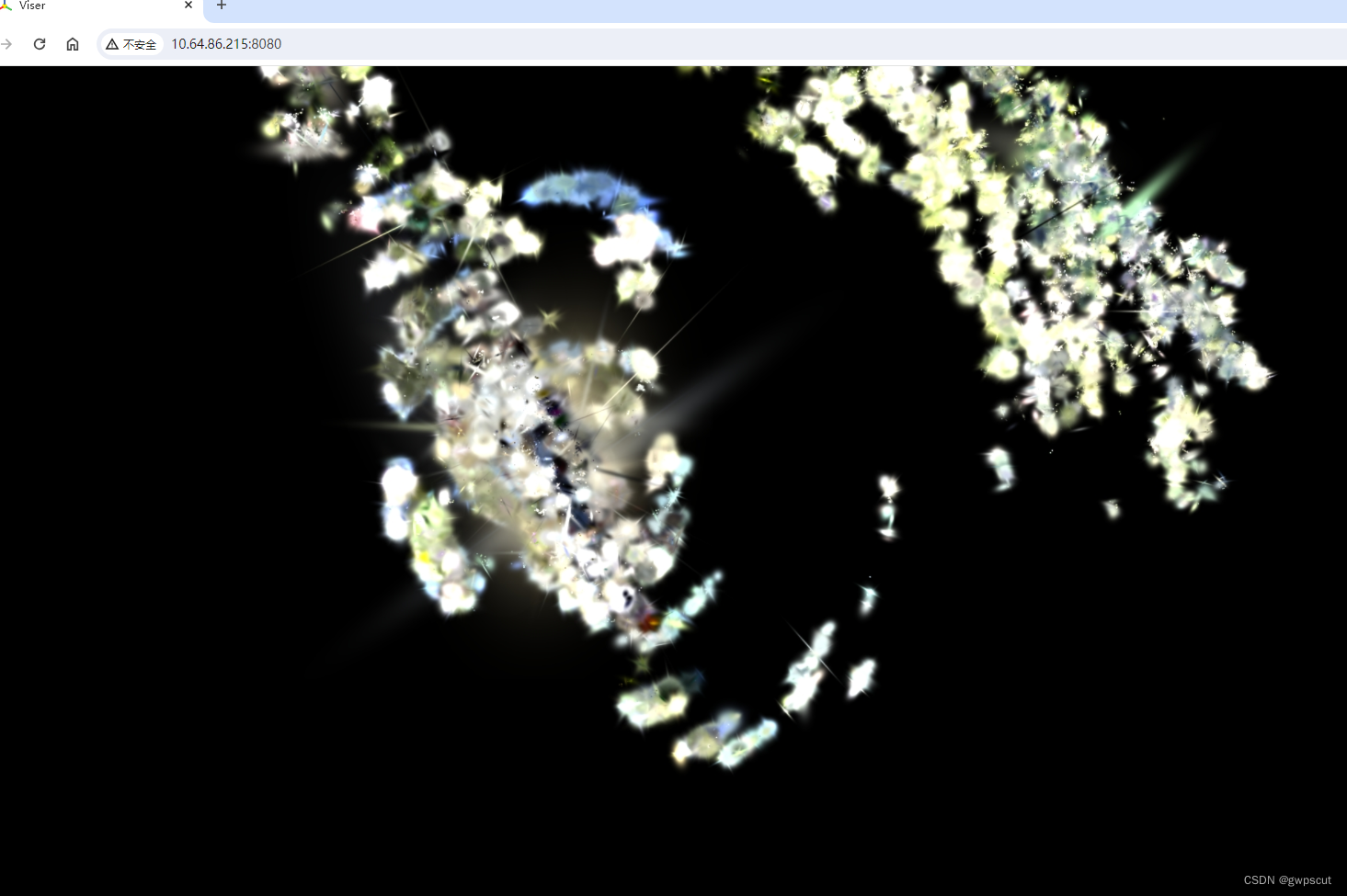
最终把渲染点云生成后再用gaussian-splatting-lightning来查看
python viewer.py TRAINING_OUTPUT_PATH在本次实验中为如下：conda activate gsplpython viewer.py /home/gwp/2d-gaussian-splatting/output/tandt/train/point_cloud/iteration_30000/point_cloud.ply出来的不知道是什么鬼。。。
换个数据集再测试看看~
#测试chair数据集
python train.py -s /home/gwp/dataset/chair -m output/chair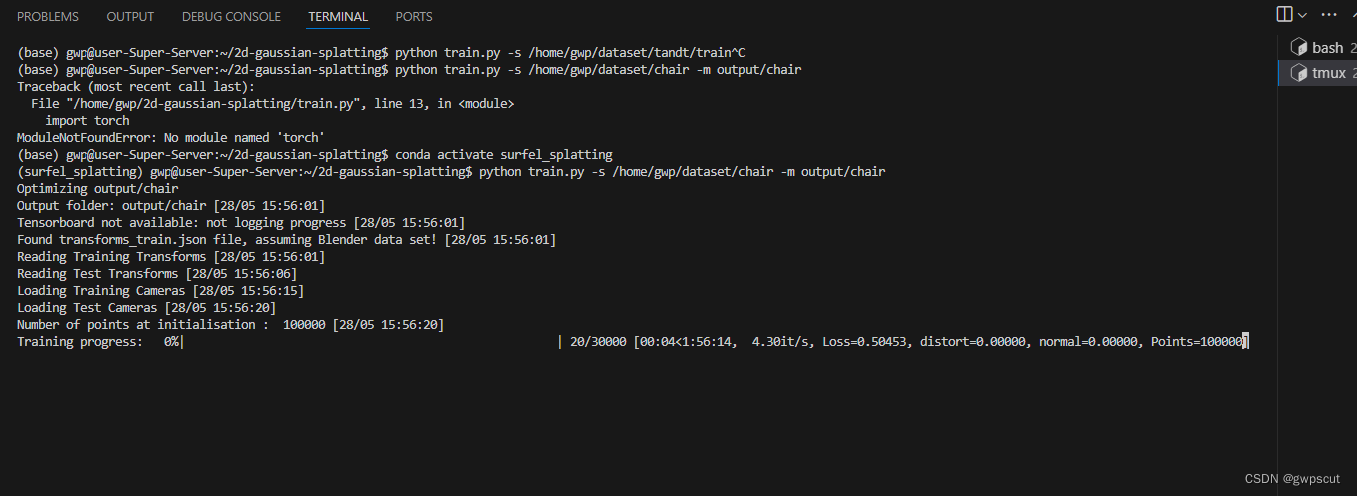
后续把训练结果放上来~
代码解读
类似3DGS系列的博客，关于2DGS的代码解读后续会push到github仓库~
参考材料
2D Gaussian Splatting论文阅读笔记 - 知乎
更多关于3DGS的介绍及解读请见：
http://t.csdnimg.cn/ZwV2r
http://t.csdnimg.cn/ZwV2r
这篇关于学习笔记之——2D Gaussian Splatting（2DGS）的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！
