本文主要是介绍24.5.26(树链剖分板子,二分+线段树),希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
星期一:
补重庆科技 C 二分 牛客传送门

思路:二维前缀和表示到第 i个人第 j个弹巢开了多少发,和st【i】表示第 i个人开的是第几个弹巢
对于 l和r的查询,使用前缀和二分找出第一个中枪的人,但因为题意第 l个人开的是1号弹巢,所以弹巢编号会有一个偏移,例如st【l】==5,那么偏移量就为4
这个偏移量在check中的使用也卡了我好一会儿,但感觉是我的问题,其实挺简单。例如py==4,查询 1号弹巢时,实际上应该看sum中的 5号弹巢有无射击,因为预处理中 l开的是 5号弹巢,实际开的是 1号,从 l到 r的所有人都会存在这个偏移
代码如下:
const int N=2e6+10,M=210;
const ll INF=0x3f3f3f3f3f3f3f3f;
const int mod=1e9+7;
ll n;
int m;
int b[N],a[N];
int sum[N][22],st[N];
int py,tl;
bool mp[22];
bool check(int x){for(int i=1;i<=m;i++){int j=(i+py-1)%m+1; //偏移量的处理if(mp[i] && sum[x][j]-sum[tl][j]) return 1; //有人出子弹了}return 0;
}
void solve(){int q; cin >> m >> n >> q;for(int i=1;i<=m;i++){cin >> b[i];mp[i]=b[i];}for(int i=1;i<=n;i++){cin >> a[i];a[i]%=m;}int box=1;sum[1][1]=1,st[1]=1;for(int i=2;i<=n;i++){box=(box+a[i-1]-1)%m+1;st[i]=box;for(int j=1;j<=m;j++) sum[i][j]=sum[i-1][j];sum[i][box]++;}while(q--){int l,r; cin >> l >> r;py=st[l]-1; //弹匣偏移量int res=0; tl=l-1;while(l<=r){int mid=l+r>>1;if(check(mid)) res=mid,r=mid-1;else l=mid+1;}if(!res) cout << "No one died\n";else cout << res << "\n";}
}武汉纺织 A 牛客传送门

赛时没出我的,第一重循环优化了下加了个continue,把自己坑了,不加continue两重循环足够了,加了continue后还得第三重循环枚举公约数,但当时光想着continue能剪枝
思路:第一重循环从m开始枚举公约数,第二重循环算 k,算出来的数的gcd不一定就是 i,开个变量gc去维护一下其gcd
代码如下:
const int N=2e6+10,M=210;
ll n;
int b[N];
bool cmp1(PII a,PII b){if(a.first!=b.first) return a.first>b.first;else return a.second<b.second;
}
void solve(){int m; cin >> n >> m;int ma=0;for(int i=1;i<=n;i++){int x; cin >> x;b[x]++;ma=max(x,ma);}vector<PII>ve;for(int i=m;i<=ma;i++){int t=0,gc=0;for(int j=i;j<=ma;j+=i){if(b[j]){t+=b[j];gc=__gcd(j,gc);}}if(t>1) ve.push_back({t,gc});}sort(ve.begin(),ve.end(),cmp1);if(!ve.empty()) cout << ve[0].first << " " << ve[0].second << "\n";else cout << "0 0\n";
}补cf 945 div2 C 构造 cf传送门

题意:给一个排列p,输出一个排列q,设a【i】= p【i】+ q【i】,使存在最多 a【i】大于两侧值
思路:可看出峰值的数量是固定的,为 n/2-1,头尾不可为峰,连续俩数不能都为峰,假如我们让奇数位置的值为峰( 除了头,发现如果p的 n值在偶数位,且挨着1,是无法实现的,但其实也不难解决,将p翻转后 n下标的奇偶性就会改变( 最后输出前记得翻转 q
解决了n的问题后就很好操作了,我们把 1 - n/2的值给偶数位,n/2+1 - n的给奇数位,越小的p加上越大的q,这样偶数位最高为 n,奇数位最少为 n+1,即满足题意
代码如下:
const int N=2e6+10,M=210;
ll n;
int p[N],pos[N],q[N];
void solve(){cin >> n;for(int i=1;i<=n;i++){cin >> p[i];pos[p[i]]=i;}bool ifr=0;if(!(pos[n]&1)){ //n在偶数位,将其翻转ifr=1;reverse(p+1,p+n+1);for(int i=1;i<=n;i++) pos[p[i]]=i;}vector<int>od,ev;for(int i=n;i;i--)i<=n/2?ev.push_back(i):od.push_back(i);int ido=0,ide=0;for(int i=1;i<=n;i++){if(pos[i]&1) q[pos[i]]=od[ido++];else q[pos[i]]=ev[ide++];}if(ifr) reverse(q+1,q+n+1); //记得判断是否翻转过pfor(int i=1;i<=n;i++) cout << q[i] << " \n"[i==n];
}dp题单 换根dp第三题 cf传送门

换根板子题,10min出了,不多讲
代码如下:
const int N=2e6+10,M=210;
ll n;
ll a[N],sum[N],dp[N],tot;
int dep[N];
vector<int>ve[N];
void dfs1(int x,int fa){if(fa) dep[x]=dep[fa]+1;sum[x]=a[x];for(int i:ve[x]){if(i==fa) continue;dfs1(i,x);sum[x]+=sum[i];}
}
void dfs2(int x,int fa){for(int i:ve[x]){if(i==fa) continue;dp[i]=dp[x]-sum[i]+tot-sum[i]; //i为根子树距离减一,其余所有节点距离加一dfs2(i,x);}
}
void solve(){cin >> n;for(int i=1;i<=n;i++){cin >> a[i];tot+=a[i];}for(int i=1;i<n;i++){int u,v; cin >> u >> v;ve[u].push_back(v);ve[v].push_back(u);}dfs1(1,0);for(int i=1;i<=n;i++) dp[1]+=1ll*dep[i]*a[i];dfs2(1,0);ll ans=0;for(int i=1;i<=n;i++) ans=max(dp[i],ans);cout << ans;
}星期二:
下午19届黑龙江,止步5题
补 F cf传送门

题意:在图上找一条包含点数不超过5的简单路径,输出点集最大权值和
思路:路径长度不超过5,可以把长度为3的路径存下来,然后遍历两头的点往两边延伸,遍历只需要遍历权值前四的点,因为极端情况下,端点找出去最多三个点可能重复,为中间点,另一端点,另一端点延伸的点,所以前四一定可以覆盖最优情况
代码如下:
ll n;
ll a[5050];
vector<int>ve[5050];
struct nod{int p1,p2,p;
};
vector<nod>tri;
bool cmp1(int x,int y){return a[x]>a[y];
}
void solve(){int m; cin >> n >> m;for(int i=1;i<=n;i++) cin >> a[i];ll ans=0;for(int i=1;i<=m;i++){int u,v; cin >> u >> v;ve[u].push_back(v);ve[v].push_back(u);ans=max(a[u]+a[v],ans);}for(int i=1;i<=n;i++){for(auto p1:ve[i]){for(auto p2:ve[i])if(p1!=p2) tri.push_back({p1,p2,i});}}for(int i=1;i<=n;i++) sort(ve[i].begin(),ve[i].end(),cmp1);for(auto t:tri){int p1=t.p1,p2=t.p2,p=t.p;if(p1==p2 || p1==p || p2==p) continue;ll sum=a[p1]+a[p2]+a[p];ans=max(sum,ans);for(int i=0,sz1=ve[p1].size();i<min(sz1,4);i++){for(int j=0,sz2=ve[p2].size();j<min(sz2,4);j++){int to1=ve[p1][i],to2=ve[p2][j];if(to1==p2 || to2==p1) continue;if(to1==p || to2==p || to1==to2) continue;ans=max(sum+a[to1]+a[to2],ans);}}for(int i=0,sz=ve[p1].size();i<min(sz,4);i++){int to=ve[p1][i];if(to==p || to==p2) continue;ans=max(sum+a[to],ans);}for(int i=0,sz=ve[p2].size();i<min(sz,4);i++){int to=ve[p2][i];if(to==p || to==p1) continue;ans=max(sum+a[to],ans);}}cout << ans;
}星期三:
补19届黑龙江 C 树链剖分

补题失败,先记着
星期四:
早上和os vp了24江苏,4题298,铜首,少wa两发就是银尾,总结下经验
24江苏 G(吃了3发罚时 cf传送门

大量的大整数输入尽量不要用double存,会很慢,因此 t了两发
整数没有确定不会爆 int就开 ll,double改成 int后 wa了一发
os写二分check的细节失误,wa了一发
后两发是完全可以避免的
!!!!!!!!!!!!!!!!警钟长鸣!!!!!!!!!!!!!!!!!!
24江苏 K 博弈 cf传送门

思路:首先能想到如果只有1,那么1的奇偶性决定胜负,但如果存在2,那么最后一个删2的人就能决定1的奇偶性,即决定谁胜。那如果存在3呢,那么最后一个删3的人就能决定2的奇偶性,即决定谁能最后删2,即决定谁胜。 推导到此即可大胆猜出结论,胜负由最大数的奇偶性决定
银牌题就是主席树,线段树也写了,确实倒腾不出来
树链剖分板子题(附线段树区修,区查板子 洛谷传送门

思路:树链剖分+线段树维护 推荐教学视频( 阿b传送门
代码如下:
const int N=2e6+10,M=210;
const int mod=1e9+7;
ll n;
int fa[N],dep[N],top[N],sz[N],son[N],dfn[N],tim;
ll v[N];
int m,r,p;
vector<int>ve[N];
struct seg_Tree{
#define lc p<<1
#define rc p<<1|1struct nod{int l,r;ll sum,add;}t[N];ll ql,qr,a[N];nod merge(nod a,nod b){nod res;res.l=a.l,res.r=b.r;res.sum=a.sum+b.sum;res.add=0;return res;}void pushup(int p){t[p]=merge(t[lc],t[rc]);}void pushdn(int p){if(!t[p].add) return ;t[lc].sum+=(t[lc].r-t[lc].l+1)*t[p].add;t[rc].sum+=(t[rc].r-t[rc].l+1)*t[p].add;t[lc].add+=t[p].add;t[rc].add+=t[p].add;t[p].add=0;}void bd(int p,int l,int r){t[p]={l,r,0,0};if(l==r){t[p].sum=a[l];return ;}int m=l+r>>1;bd(lc,l,m);bd(rc,m+1,r);pushup(p);}void update(int p,int v){if(ql<=t[p].l && qr>=t[p].r){t[p].sum+=1ll*(t[p].r-t[p].l+1)*v;t[p].add+=v;return ;}int m=t[p].l+t[p].r>>1;pushdn(p);if(ql<=m) update(lc,v);if(qr>m) update(rc,v);pushup(p);}nod query(int p){if(ql<=t[p].l && qr>=t[p].r) return t[p];int m=t[p].l+t[p].r>>1;pushdn(p);if(ql>m) return query(rc);if(qr<=m) return query(lc);return merge(query(lc),query(rc));}void updt(int l,int r,int v){ql=l;qr=r;
// qop=op;update(1,v);}ll ask(int l,int r){ql=l,qr=r;return query(1).sum;}
#undef lc
#undef rc
}tr;
void dfs1(int x,int f){fa[x]=f;dep[x]=dep[f]+1;sz[x]=1;int ts=0;for(int i:ve[x]){if(i==f) continue;dfs1(i,x);sz[x]+=sz[i];if(sz[i]>ts) ts=sz[i],son[x]=i;}
}
void dfs2(int x,int t){dfn[x]=++tim;tr.a[tim]=v[x];top[x]=t;if(!son[x]) return ;dfs2(son[x],t);for(int i:ve[x]){if(i==son[x] || i==fa[x]) continue;dfs2(i,i); //注意dfs2的第二个参数也是i}
}
void update(int x,int y,int z){z%=p;while(top[x]!=top[y]){if(dep[top[x]]<dep[top[y]]) swap(x,y);tr.updt(dfn[top[x]],dfn[x],z);x=fa[top[x]];}if(dep[x]>dep[y]) swap(x,y);tr.updt(dfn[x],dfn[y],z);
}
ll query(int x,int y){ll res=0;while(top[x]!=top[y]){if(dep[top[x]]<dep[top[y]]) swap(x,y);res+=tr.ask(dfn[top[x]],dfn[x]),res%=p;x=fa[top[x]];}if(dep[x]>dep[y]) swap(x,y);res+=tr.ask(dfn[x],dfn[y]);return res%p;
}
void solve(){cin >> n >> m >> r >> p;for(int i=1;i<=n;i++) cin >> v[i];for(int i=1;i<n;i++){int u,v; cin >> u >> v;ve[u].push_back(v);ve[v].push_back(u);}dfs1(r,r);dfs2(r,r);tr.bd(1,1,n);while(m--){int op,x; cin >> op >> x;if(op==1){int y,z; cin >> y >> z;update(x,y,z);}else if(op==2){int y; cin >> y;cout << query(x,y) << "\n";}else if(op==3){int z; cin >> z;tr.updt(dfn[x],dfn[x]+sz[x]-1,z);}else cout << tr.ask(dfn[x],dfn[x]+sz[x]-1)%p << "\n"; //记得取模}
}晚上vp了下24长春邀请赛,出了3题就做不动了,很累。。
补ABC292 Ex atc传送门

思路:线段树维护最大前缀和,然后二分,这是 O(n*(logn)^2)的做法
如果没有B这个条件,那么我们只需要知道得分总和,rating即为sum/n
但存在B的条件后,我们需要知道第一个rating>=B的点,对式子进行如下演化
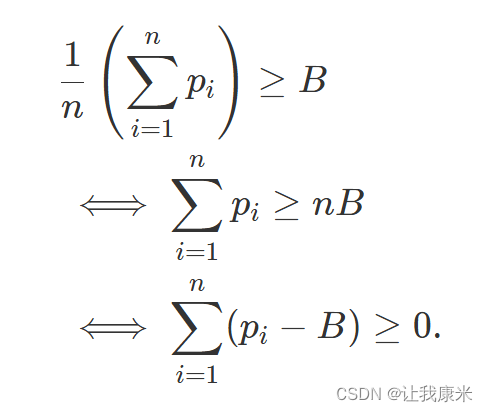
我们可以对于 pi-B的值做一个前缀和,然后找到第一个前缀和>=0的点即可
但是问题是,前缀和并不具有单调性,如何才能快速找到第一个点呢?
这里要引进线段树的一个新功能,维护最大前缀和,which具有单调性,即可进行二分查询
代码如下:
const int N=2e6+10,M=210;
ll n;
ll b;
struct seg_Tree{
#define lc p<<1
#define rc p<<1|1struct nod{int l,r;ll sum,pre;}t[N];int ql,qr; //查询区间nod merge(nod a,nod b){nod res;res.l=a.l,res.r=b.r;res.sum=a.sum+b.sum;;res.pre=max(a.sum+b.pre,a.pre);return res;}void pushup(int p){t[p]=merge(t[lc],t[rc]);} //向上更新void bd(int p,int l,int r){ //bd里处理输入if(l==r){t[p]={l,r,0,0};cin >> t[p].sum;t[p].sum-=b;t[p].pre=t[p].sum;return ;}int m=l+r>>1;bd(lc,l,m);bd(rc,m+1,r);pushup(p);}void update(int p,int v){if(ql<=t[p].l && qr>=t[p].r){t[p].sum=v-b; //叶子节点的所有信息都要改t[p].pre=t[p].sum;return ;}int m=t[p].l+t[p].r>>1;if(ql<=m) update(lc,v);if(qr>m) update(rc,v);pushup(p); //向上更新}nod query(int p){if(ql<=t[p].l && qr>=t[p].r) return t[p];int m=t[p].l+t[p].r>>1;if(ql>m) return query(rc);if(qr<=m) return query(lc);return merge(query(lc),query(rc));}void updt(int l,int r,int v){ql=l;qr=r;
// qop=op;update(1,v);}ll ask_pre(int l,int r){ql=l,qr=r;return query(1).pre;}ll ask_sum(int l,int r){ql=l,qr=r;return query(1).sum;}
#undef lc
#undef rc
}tr;
void solve(){cout << fixed << setprecision(13);int q; cin >> n >> b >> q;tr.bd(1,1,n);while(q--){int c,x; cin >> c >> x;tr.updt(c,c,x);int l=1,r=n,res=n;while(l<=r){ //二分找到第一个pre>=0的点int mid=l+r>>1;if(tr.ask_pre(1,mid)>=0) res=mid,r=mid-1;else l=mid+1;}cout << 1.0*(tr.ask_sum(1,res)+1ll*res*b)/res << "\n";}
}星期五:
补24长春邀请赛 B 树形dp cf传送门

题意:找出一种dfs的方式,使得dfs序中偶数下标节点的权值和最大
思路:很明显的树形dp,但赛时因脑力不足只定了个状态,没有更细想如何转移
dp【i】【0/1】表示以偶数/奇数顺序进入 i节点的最大答案,dp【1】【1】为答案
偶数sz的子节点,不会影响奇偶顺序,一个奇子节点会影响一次
如果只有偶数子节点,那么0/1的选择是固定的,如果存在奇节点,所有偶节点可以取更大值,对于奇节点的选择,如果偶数个奇节点,0/1各一半,如果奇数个,多的那个取父节点的反,将奇点的 0/1 差值排个序,贪心即可
代码如下:
const int N=2e6+10,M=210;
ll n;
ll dp[N][2],a[N];
int sz[N];
vector<int>ve[N];
bool cmp1(int a,int b){return dp[a][0]-dp[a][1]>dp[b][0]-dp[b][1];
}
void dfs(int x,int f){dp[x][0]=a[x];dp[x][1]=0;sz[x]=1;bool if1=0;for(int i:ve[x]){if(i==f) continue;dfs(i,x);sz[x]+=sz[i];if(sz[i]&1) if1=1;}if(!if1){for(int i:ve[x]){if(i==f) continue;dp[x][1]+=dp[i][0];dp[x][0]+=dp[i][1];}}else{vector<int>son;for(int i:ve[x]){if(i==f) continue;if(sz[i]&1) son.push_back(i);else{dp[x][1]+=max(dp[i][0],dp[i][1]);dp[x][0]+=max(dp[i][0],dp[i][1]);}}sort(son.begin(),son.end(),cmp1);if(son.size()&1){for(int i=0,ssz=son.size();i<ssz;i++){if(i<ssz/2) dp[x][0]+=dp[son[i]][0],dp[x][1]+=dp[son[i]][0];else if(i==ssz/2) dp[x][0]+=dp[son[i]][1],dp[x][1]+=dp[son[i]][0];else dp[x][0]+=dp[son[i]][1],dp[x][1]+=dp[son[i]][1];}}else{for(int i=0,ssz=son.size();i<ssz;i++){if(i<ssz/2) dp[x][0]+=dp[son[i]][0],dp[x][1]+=dp[son[i]][0];else dp[x][0]+=dp[son[i]][1],dp[x][1]+=dp[son[i]][1];}}}
}
void solve(){cin >> n;for(int i=1;i<=n;i++) ve[i].clear();for(int i=1;i<=n;i++) cin >> a[i];for(int i=1;i<n;i++){int u,v; cin >> u >> v;ve[u].push_back(v);ve[v].push_back(u);}dfs(1,0);cout << dp[1][1] << "\n";
}easy线段树题 建平台 洛谷传送门

思路:线段树维护区间高度,需支持区间修改和单点查询
代码如下:
const int N=2e6+10,M=210;
ll n;
struct seg_Tree{
#define lc p<<1
#define rc p<<1|1struct nod{int l,r;int hei,add;}t[N];int ql,qr,qv;nod merge(nod a,nod b){nod res;res.l=a.l,res.r=b.r;res.hei=max(a.hei,b.hei); // useless,因为查询高度只会是单点res.add=0;return res;}void pushup(int p){t[p]=merge(t[lc],t[rc]);}void pushdn(int p){if(!t[p].add) return ;t[lc].hei=t[p].add;t[rc].hei=t[p].add;t[lc].add=t[p].add;t[rc].add=t[p].add;t[p].add=0;}void bd(int p,int l,int r){t[p]={l,r,0,0};if(l==r) return ;int m=l+r>>1;bd(lc,l,m);bd(rc,m+1,r);pushup(p);}void update(int p){if(ql<=t[p].l && qr>=t[p].r){t[p].hei=qv;t[p].add=qv;return ;}int m=t[p].l+t[p].r>>1;pushdn(p);if(ql<=m) update(lc);if(qr>m) update(rc);pushup(p);}nod query(int p){if(ql<=t[p].l && qr>=t[p].r) return t[p];int m=t[p].l+t[p].r>>1;pushdn(p);if(qr<=m) return query(lc);if(ql>m) return query(rc);return merge(query(lc),query(rc));}void updt(int l,int r,int v){ql=l,qr=r;qv=v;update(1);}int ask_hei(int l,int r){ql=l,qr=r;return query(1).hei;}
#undef lc
#undef rc
}tr;
struct nod{int l,r,y;
}bo[110];
void solve(){cin >> n;int ma=0;for(int i=1;i<=n;i++){cin >> bo[i].y >> bo[i].l >> bo[i].r;bo[i].l++;ma=max(bo[i].r,ma);}tr.bd(1,1,ma);sort(bo+1,bo+n+1,[](nod a,nod b){return a.y<b.y;}); //按高度排序ll ans=0;for(int i=1;i<=n;i++){int h=bo[i].y;ans+=h-tr.ask_hei(bo[i].l,bo[i].l)+h-tr.ask_hei(bo[i].r,bo[i].r);tr.updt(bo[i].l,bo[i].r,h);}cout << ans;
}dp题单 状压dp第五题 鱼吃鱼 cf传送门

题意:n条鱼,每次两条鱼相遇且有一条被对方吃掉,n*n矩阵 aij为 i鱼吃掉 j鱼概率,问每条鱼活到最后的期望是多少
思路:dp【mask】表示状态为mask的期望,先设定全1期望为1,然后倒着枚举状态,对于每一个状态,先枚举被吃掉的0,再枚举吃掉它的1
dp【mask】+= 原状态期望*两鱼相遇概率* j吃掉 i的概率
代码如下:
ll n;
double dp[1<<19];
double a[19][19];
ll c(int n,int m){ll res=1;for(int i=1;i<=m;i++)res=res*(i+n-m)/i;return res;
}
void solve(){cout << fixed << setprecision(8);cin >> n;for(int i=0;i<n;i++){for(int j=0;j<n;j++) cin >> a[i][j];}dp[(1<<n)-1]=1;for(int mask=(1<<n)-1;mask;mask--){ //状态倒着枚举for(int i=0;i<n;i++){if(mask>>i&1) continue;for(int j=0;j<n;j++){if(!(mask>>j&1)) continue;int nmask=mask|(1<<i); //i被吃掉前的状态dp[mask]+=dp[nmask]*1.0/c(__builtin_popcount(nmask),2)*a[j][i];}}}for(int i=0;i<n;i++) cout << dp[1<<i] << " ";
}星期六:
线段树区间乘区间加区间查询 模板 洛谷传送门
思路:需要两个懒标记,一个负责区间加,一个负责区间乘,注意mul对add的影响
对于存在add的区间再进行乘操作后,区间应是(sum+len*add)*k,分配后为sum*k+len*add*k,所以不仅mul*=k,add也需*=k,pushdn时先处理mul再add(因为add已经乘过了
代码如下:
const int N=2e6+10,M=210;
ll n;
int m;
struct seg_Tree{
#define lc p<<1
#define rc p<<1|1struct nod{int l,r;ll sum,add,mul; //区间和,加法懒标记,乘法懒标记}t[N];ll ql,qr,qv,qop;nod merge(nod a,nod b){nod res;res.l=a.l,res.r=b.r;res.sum=a.sum+b.sum;res.add=0;res.mul=1;return res;}void pushup(int p){t[p]=merge(t[lc],t[rc]);}void pushdn(int p){ //注意先乘再加t[lc].sum*=t[p].mul,t[lc].sum+=(t[lc].r-t[lc].l+1)*t[p].add,t[lc].sum%=m;t[rc].sum*=t[p].mul,t[rc].sum+=(t[rc].r-t[rc].l+1)*t[p].add,t[rc].sum%=m;t[lc].add*=t[p].mul,t[lc].add+=t[p].add,t[lc].add%=m;t[rc].add*=t[p].mul,t[rc].add+=t[p].add,t[rc].add%=m;t[lc].mul*=t[p].mul,t[lc].mul%=m;t[rc].mul*=t[p].mul,t[rc].mul%=m;t[p].add=0,t[p].mul=1;}void bd(int p,int l,int r){t[p]={l,r,0,0,1};if(l==r){cin >> t[p].sum;return ;}int m=l+r>>1;bd(lc,l,m);bd(rc,m+1,r);pushup(p);}void update(int p){if(ql<=t[p].l && qr>=t[p].r){if(qop==1){t[p].sum*=qv,t[p].sum%=m; t[p].mul*=qv,t[p].mul%=m;t[p].add*=qv,t[p].add%=m;}else{t[p].sum+=1ll*(t[p].r-t[p].l+1)*qv,t[p].sum%=m;t[p].add+=qv,t[p].add%=m;}return ;}int mid=t[p].l+t[p].r>>1;pushdn(p);if(ql<=mid) update(lc);if(qr>mid) update(rc);pushup(p);}nod query(int p){if(ql<=t[p].l && qr>=t[p].r) return t[p];int m=t[p].l+t[p].r>>1;pushdn(p);if(ql>m) return query(rc);if(qr<=m) return query(lc);return merge(query(lc),query(rc));}void updt(int l,int r,int op,int v){ql=l;qr=r;qv=v;qop=op;update(1);}ll ask(int l,int r){ql=l,qr=r;return query(1).sum;}
#undef lc
#undef rc
}tr;这篇关于24.5.26(树链剖分板子,二分+线段树)的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!



