本文主要是介绍ABAQUS应用07-实现拉伸和压缩刚度不同的弹簧建模,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
文章目录
- 0、背景描述
- 1、步骤
0、背景描述
到目前为止,本文的内容我还没有具体实践过,但是个人认为后期是会用到的。比如说,对于风电机组地基转动刚度的设置,土体就是一种拉压刚度并不相同的材料。所以现在先记录下来,后期用得到再来翻找。想要看原文的,可以点击这里。感谢原作者的分享。
1、步骤
可以通过使用交互模块中的特殊菜单来定义弹簧/阻尼器功能,从而在两点之间定义弹簧元素:
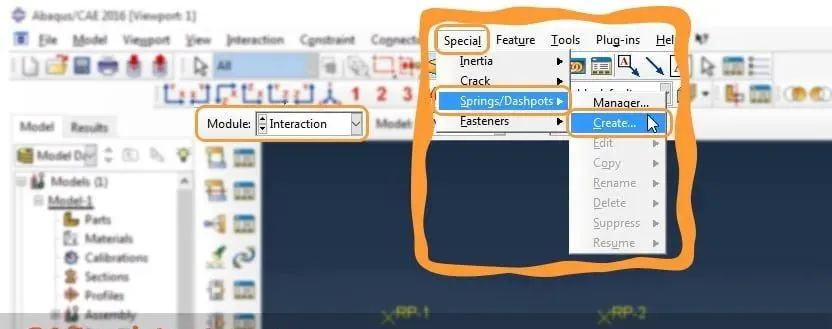
(在这里,为了拥有一个非常简单的模型,我们之前在 Assembly 模块中定义了两个参考点。)
在选择两点后出现的“编辑弹簧/阻尼器”窗口中,您可以定义弹簧刚度:
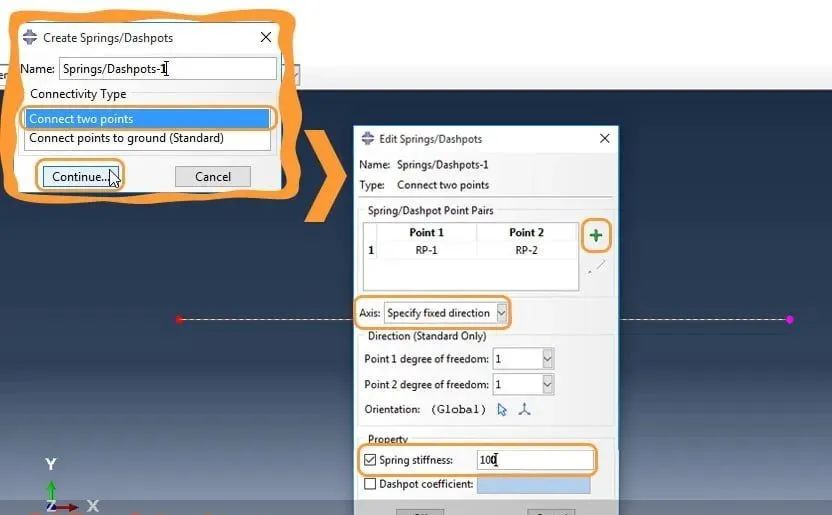
该刚度对于拉伸和压缩来说是相同的。如果您想定义不同的拉伸和压缩刚度,则必须使用 Abaqus 关键字编辑器修改关键字:

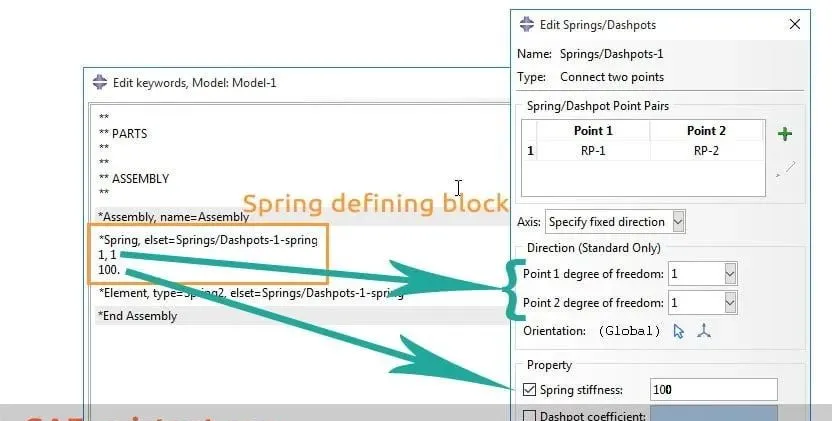
现在,您可以在创建弹簧时通过 Abaqus/CAE 中的图形命令看到 Abaqus 自动创建的关键字:
*Spring,elset=SpringsDashpot-1-spring,nonlinear
1,1
200,-1
0,0
100,1
通过在弹簧定义块中添加非线性项(*Spring 关键字),我们可以定义压缩和拉伸时不同的弹簧行为。只需单击 *Spring… 行并编辑该块,如下所示:
(当你开始编辑时,受影响的块的颜色会变成粉红色)
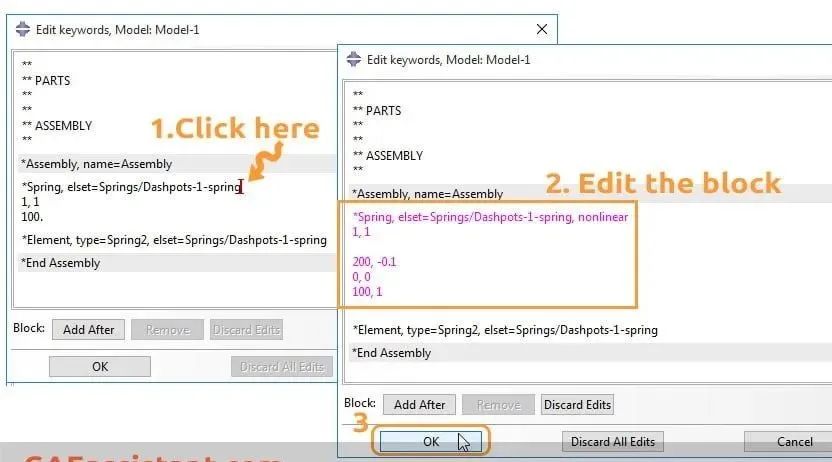
添加的数据线为:
力1,位移-1
0.0, 0.0
力 3、位移 3
这意味着当您施加 -1.0 m 位移时,弹簧将产生 200 N 的力,因此 K=F/x=200/1=200 N/m;这是压缩时的刚度。然后,您可以通过 100 N 力的 1.0 m 位移来定义拉伸刚度,即 K=100 N/m。
这篇关于ABAQUS应用07-实现拉伸和压缩刚度不同的弹簧建模的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!








