2020icpc专题
2020ICPC南京站补题题解
菜鸡只写银牌以下的题 这场铜牌4题,银牌5~6题 K Co-prime Permutation 题意: 构造一个n长的1到n不重复序列p,其中 p i p_i pi和 i i i互质的个数有k个 思路: 已知: n n n和 n − 1 n-1 n−1互质,1和任何数互质,任何数和它本身不互质 k要是奇数,1不变,后面的 k − 1 2 \frac{k-1}{2} 2k−1对数,两两换
2020ICPC·小米 网络选拔赛第二场 Determinant(行列式)
题意: 按照题目规则组成的矩阵,求行列式值。 思路: 流下了不会线代的泪水,虽然最后推出来了,但是签到题那么久不应该。 按照行列式的性质可以有如下变化 1 2 3 4 5 + x 6 7 8 9 \begin{matrix} 1 & 2 & 3 \\ 4 & 5+x & 6 \\ 7 & 8 & 9 \end{matrix} 14725+x8369 => 1 2 3 4 5
2020ICPC 南京 Monster Hunter(树形依赖背包)
好久没写树形DP手生疏了。 题意: 每个点权值为 h p [ x ] + h p [ v ] hp[x]+hp[v] hp[x]+hp[v],其中 v v v是 x x x的儿子。你可以删掉 m m m个点,求对于 0 ≤ m ≤ n 0≤m≤n 0≤m≤n的每个 m m m能得到的最小权值和。 思路: 定义 d p [ i ] [ j ] [ 0 / 1 ] dp[i][j][0/1] dp
2020ICPC 南京 Evil Coordinate(模拟,构造)
最后是队友过的,我写的相对复杂 题意: 给一个移动的序列(L,R,U,D代表左右上下), 重排其使得移动的过程不会经过 ( X , Y ) (X,Y) (X,Y)。 设终点为 ( e x , e y ) (ex,ey) (ex,ey) 思路: 首先特判掉特殊点为终点或者为原点的情况, 分为两种情况: 特殊点不在坐标轴上,此时如果 e x = X ex=X ex=X,那么先用 L , R L,
2020ICPC 南京 K Co-prime Permutation(构造)
题意: 构造一个排列,使得 g c d ( i , p i ) = 1 gcd(i,p_i)=1 gcd(i,pi)=1的 p i p_i pi数目严格为 k k k。 思路: 因为 1 1 1的存在,所以 k k k一定不会是0。 因为 g c d ( x , x + 1 ) = 1 gcd(x,x+1)=1 gcd(x,x+1)=1,所以只需要交换相邻两个数就可以使得结果加2。 当 k
2020ICPC上海 Fibonacci(水过)
康复训练,水水代码证明我还活着。 思路: 可以发现斐波那契数列数列是奇奇偶、奇奇偶这样排列的。 所以3个数分为一组,假设为 k k k组。 偶数和后面的数组合的 g g g值都为1。 第一个偶数有 n − 3 n-3 n−3个组合 第二个有 n − 3 ∗ 2 n-3*2 n−3∗2个组合 第三个有 n − 3 ∗ 3 n-3*3 n−3∗3个组合 。。。 直到最后一个有 n − 3 ∗ k
2020ICPC·小米 网络选拔赛第一场 Router Mesh
题目链接 https://ac.nowcoder.com/acm/contest/7501 题意 求出图中删去每个点后联通块数目 思路 tarjan算法求割点修改 维护dfn和low数组,对于边u-v,如果low[v]>=dfn[u],说明只可以通过u到达v,u是割点,删除u会增加一个连通数,那我们记录增加的连通数个数,记为tmp。当u不是树根时,删点后父亲也是一个分量,那么删去后联通
2020ICPC 江西省大学生程序设计竞赛 A Simple Math Problem
题目: 题目链接: 题解: 莫比乌斯反演 推导过程如下 ∑ i = 1 n ∑ j = 1 i F [ j ] [ g c d ( i , j ) = 1 ] \sum_{i=1}^{n}\sum_{j=1}^{i} {F[j][gcd(i,j)=1]} ∑i=1n∑j=1iF[j][gcd(i,j)=1] 可以转化为 ∑ i = 1 n F [ i ] ∑ j = i n g
2020ICPC·小米 网络选拔赛第一场题解(D,J)
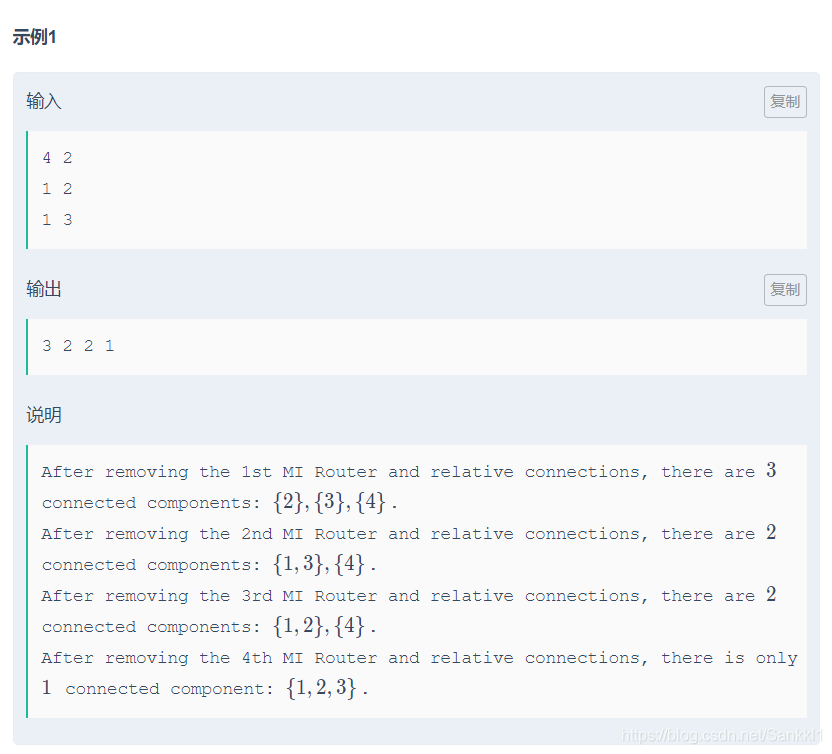
链接:https://ac.nowcoder.com/acm/contest/7501 来源:牛客网 D-Router Mesh 时间限制:C/C++ 1秒,其他语言2秒 空间限制:C/C++ 262144K,其他语言524288K 64bit IO Format: %lld judge:牛客竞赛 In a Mesh networking system, there are n n
2020ICPC·小米 网络选拔赛第一场(重温经典)
2020ICPC·小米 网络选拔赛第一场 导语涉及的知识点题目ACDEFG 参考文献 导语 队内练习,做的并不是很好,有很多地方其实是可以完善的,比如答题策略,自己的签到居然wa了一发,可耻。 涉及的知识点 图论、二维差分、搜索、线段树、数论、dp、贪心 链接:2020ICPC·小米 网络选拔赛第一场 题目 A 题目大意:给定一个序列,选出最多的数,使得选中的数之间互
2020ICPC·小米 网络选拔赛第一场 D.Router Mesh(tarjan 割点)
题目链接:https://ac.nowcoder.com/acm/contest/7501/D tarjan的割点算法可以参考博文:https://blog.csdn.net/csyifanZhang/article/details/105370924 分析 求一个图去掉第 i 个点后的连通块数量 分析 对于每个点,首先总共有 sum 个连通块,求出每个点所在的强连通分量的个数
2020ICPC·小米 网络选拔赛第一场 J.Matrix Subtraction(二维差分)
题目链接:https://ac.nowcoder.com/acm/contest/9541/J 题目描述 Given a matrix M_{}M of size n\times mn×m and two integers a, b_{}a,b , determine weither it is possible to make all entrys of M_{}M zero by repea
2020ICPC 江西省大学生程序设计竞赛 K.Travel Expense
题意: 有 n 座城市,m 条双向道路,一条道路要走一天,每条道路的费用是 items ^ days ( items 是所携带的物品数量, days 是第几天),现在查询q次,(1-1e5)然后给你一个出发城市 S ,目的地城市 T ,预算 B ,问最多能携带多少物品。 思路: Floyd预处理每个点之间的最短路,因为长度不大所以可以跑,n^3的复杂度,然后接下来二分枚举答案,输出最优解,求
2020ICPC银川(A E G J K)
2020ICPC银川(A E G J K) 2020ICPC银川 A. Best Player(模拟) 在某一维方向上无法区分的点显然另两维坐标相同 , 那么在当前维度上能区分的点个数就是本质不同的另两维坐标组成的点对的个数 , 用set维护一下即可。 #include<bits/stdc++.h>using namespace std;#define fi first#define