172专题
Golang | Leetcode Golang题解之第172题阶乘后的零
题目： 题解： func trailingZeroes(n int) (ans int) {for n > 0 {n /= 5ans += n}return}
C语言 | Leetcode C语言题解之第172题阶乘后的零
题目： 题解： int trailingZeroes(int n) {int ans = 0;while (n) {n /= 5;ans += n;}return ans;}
172.二叉树：左叶子之和（力扣）
代码解决 /*** Definition for a binary tree node.* struct TreeNode {* int val;* TreeNode *left;* TreeNode *right;* TreeNode() : val(0), left(nullptr), right(nullptr) {}* TreeNode(in
172开头的IP不一定是局域网的地址
前些天发现了一个巨牛的人工智能学习网站，通俗易懂，风趣幽默，忍不住分享一下给大家。点击跳转到教程。 A类 10.0.0.0-10.255.255.255 网络数：1B类 172.16.0.0-172.31.255.255 网络数：16C类 192.168.0.0-192.168.255.255 网络数：255在这三种地址中间的址是非路由的IP,B类 172.16.0.0-172.31.255
深入解析力扣172题：阶乘后的零（计算因子5的方法详解及模拟面试问答）
在本篇文章中，我们将详细解读力扣第172题“阶乘后的零”。通过学习本篇文章，读者将掌握如何使用多种方法来解决这一问题，并了解相关的复杂度分析和模拟面试问答。每种方法都将配以详细的解释和ASCII图解，以便于理解。 问题描述 力扣第172题“阶乘后的零”描述如下： 给定一个整数 n，返回 n! 结果尾数中零的数量。 示例 1: 输入: 3输出: 0解释: 3! = 6, 尾数中没有零。
![[LeetCode] 172. Factorial Trailing Zeroes](/front/images/it_default.gif)
[LeetCode] 172. Factorial Trailing Zeroes
题目内容 给定一个整数 n，返回 n! 结果尾数中零的数量。 示例 1:输入: 3输出: 0解释: 3! = 6, 尾数中没有零。示例 2:输入: 5输出: 1解释: 5! = 120, 尾数中有 1 个零. 题目思路 需要思考一下，到底什么情况下会出现0。那么根据经验，只要碰到包含因子5的数字，就会出现0.（包含5然后包含偶数，而且偶数的数量大于5的个数）。比如5！包含1个
LeetCode--172. Factorial Trailing Zeroes
Problem: Given an integer n, return the number of trailing zeroes in n!. Note: Your solution should be in logarithmic time complexity. Analysis: 对n!做质因数分解n!=2x*3y*5z*… 显然0的个数等于min(x,z)，并且min(x,z
Project Euler_Problem 172_Few Repeated Digits_动态规划
原题目： 题目大意：18位数里头，有多少个数，对于每个数字0-9，在这18位里面出现均不超过3次 111222333444555666 布星~~ 112233445566778899 可以~~ 解题思路： 动态规划 代码: ll F[19][3000000];void solve() {ll i, j,k,x,y,z,p,q,u,v;ll N = 18,NN=4;double
文献阅读（172）2021 NoC论文
文章目录 题目：Topology Agnostic Virtual Channel Assignment and Protocol Level Deadlock Avoidance in a Network-on-Chip时间：2021会议：DAC研机机构：ARM 本篇论文的主要贡献： 针对虚通道Virtual Channle(VC)分配问题进行优化，将VC分配问题抽象成Traf
LCR 172. 统计目标成绩的出现次数
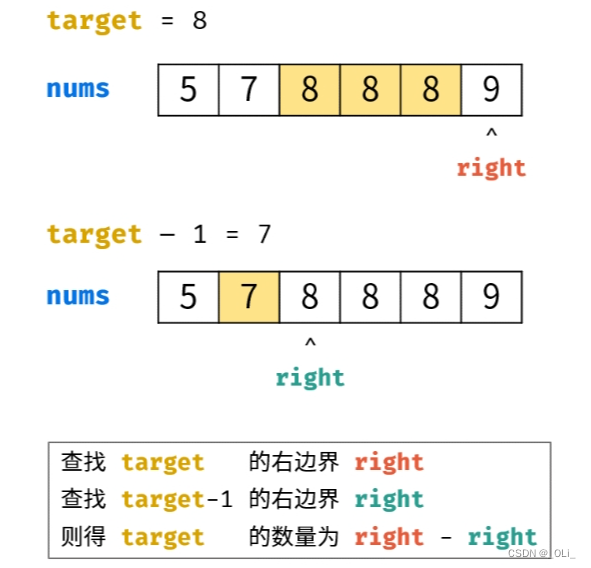
解题思路：二分查找 题解一 class Solution {public int countTarget(int[] scores, int target) {// 搜索右边界 rightint i = 0, j = scores.length - 1;while(i <= j) {int m = (i + j) / 2;if(scores[m] <= target) i
172基于matlab的MPPT智能算法
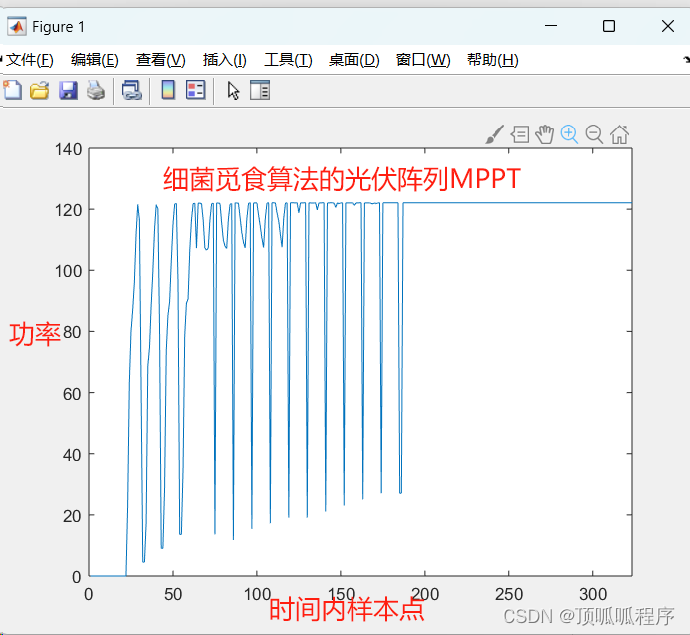
基于matlab的MPPT智能算法，通过细菌觅食进行优化。算法引入了趋向性操作，用以进行局部范围内的最优寻找；引入了复制操作，用以避免种群更新盲目随机性，加快了算法的收敛速度；引入了迁徙操作用以避免算法陷入局部最优解。分析了光伏阵列在遮挡条件下输出功率的变化特性，然后使用细菌觅食算法进行了最大功率点跟踪控制方法实验。程序已调通，可直接运行。 172 细菌觅食优化算法 光伏阵列功率变化 (xi
![[LeetCode]172.Factorial Trailing Zeroes](https://img-blog.csdn.net/20150207203556051)
[LeetCode]172.Factorial Trailing Zeroes
题目 Given an integer n, return the number of trailing zeroes in n!. Note: Your solution should be in logarithmic time complexity. 分析 朴素解法： 首先求出n!，然后计算末尾0的个数。（重复÷10，直到余数非0） 该解法在输入的数字稍大时就会导致阶乘得数溢出，
AtCoder Regular Contest 172（仅A题）
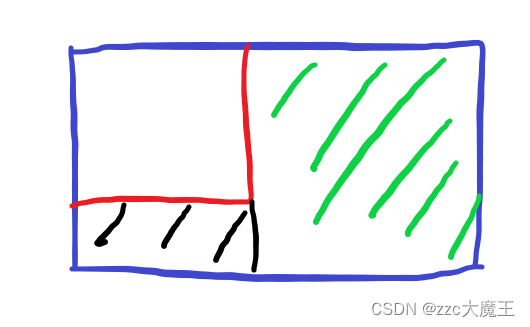
A - Chocolate 给N个人分巧克力，分的大小是2^Ai * 2^Ai，给你一个大小为H*W的巧克力，问能不能给N个人都分到要求的巧克力。 假设蓝色是h*w的大巧克力，红色的是要分出来的巧克力（四个角落都一样，这里用左上角）显然放角落会比放在中间或者其他地方带来更好的情况。 这里从最大的开始切，假设红色的就是最大的，那么把剩下的分成两块放回去用，不管是第一种还是第二种，都不会影响
[Leetcode]172. Factorial Trailing Zeroes
Given an integer n, return the number of trailing zeroes in n!. Note: Your solution should be in logarithmic time complexity. 我们对n!分解质因子，n!=2^x+3^y+5^z+...，结尾的0一定是1个2和1个5相乘得到的。很显然，这里因子5的个数小于因子2的个
基于ResNet-152模型的172种食物图像分类
转载自AI Studio 项目链接 https://aistudio.baidu.com/aistudio/projectdetail/3395323?contributionType=1&shared=1 一、项目背景和项目创意 由于计算机视觉技术在监控摄像头、医疗保健等许多领域的应用越来越多。食品识别是其中一个重要的领域，由于其现实意义和科学挑战，值得进一步研究。最近，卷积神经网络(CN
2021-03-02oracle查询当前时间，当前时间往前推七天（168个小时），当前时间往前推七天加四个小时（172个小时）
select SYSDATE,SYSDATE-numtodsinterval(168,'hour'),SYSDATE-numtodsinterval(172,'hour') FROM dual
【LGR-172-Div.4】洛谷入门赛 #19（A—H,c++详解！）
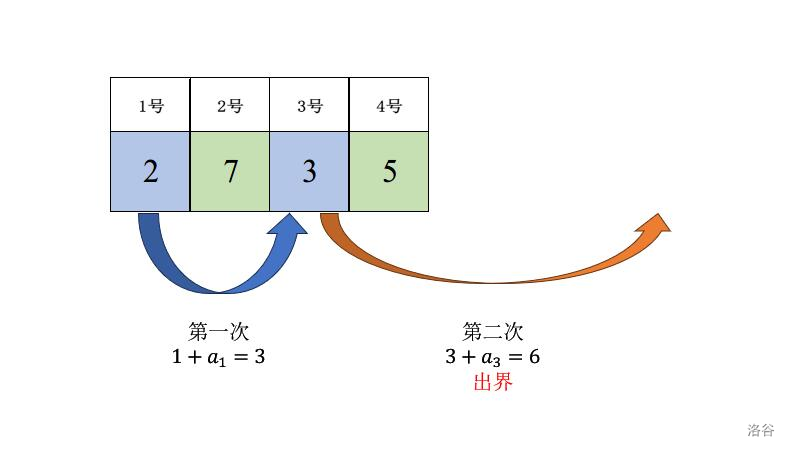
文章目录 【LGR-172-Div.4】洛谷入门赛 #19A.分饼干 I题目描述输入格式输出格式样例 #1样例输入 #1样例输出 #1 样例 #2样例输入 #2样例输出 #2 提示样例解释 1样例解释 2数据范围与约定思路: 代码 B.分饼干 II题目描述输入格式输出格式样例 #1样例输入 #1样例输出 #1 样例 #2样例输入 #2样例输出 #2 提示数据规模与约定 思路代码 C.跳房子题
172. Python语言 的 Flask框架项目 之 异步方案 Celery 第一章：生产者消费者设计模式
生产者消费者设计模式 本章主题关键词问题解决生产者消费者设计模式介绍总结小便条 本章主题 关键词 问题 我们的代码是自上而下同步执行的。发送短信是耗时的操作。如果短信被阻塞住，用户响应将会延迟。响应延迟会造成用户界面的倒计时延迟。 解决 异步发送短信发送短信和响应分开执行，将发送短信从主业务中解耦出来。 生产者消费者设计模
（172）粒子表达式
DynamicParameter（动态参数） DynamicParameter（动态参数）表达式为粒子发射器提供管道，以便将最多四个要以任意方式处理的值传递给材质。这些值是通过放置在发射器上的 ParameterDynamic 模块在 Cascade 中设置的。 项目 说明 属性 参数名称（Param Names） 参数名称的数组。这里的值将确定材质编辑器中显示在表达式输
openGauss学习笔记-172 openGauss 数据库运维-备份与恢复-导入数据-分析表172.1 分析表172.2 表自动分析
文章目录 openGauss学习笔记-172 openGauss 数据库运维-备份与恢复-导入数据-分析表172.1 分析表172.2 表自动分析 openGauss学习笔记-172 openGauss 数据库运维-备份与恢复-导入数据-分析表 执行计划生成器需要使用表的统计信息，以生成最有效的查询执行计划，提高查询性能。因此数据导入完成后，建议执行ANALYZE语句生成最新
【LintCode 简单】172. 删除元素
1.问题描述： 给定一个数组和一个值，在原地删除与值相同的数字，返回新数组的长度。 元素的顺序可以改变，并且对新的数组不会有影响。 2.样例： 给出一个数组 [0,4,4,0,0,2,4,4]，和值 4 返回 4 并且4个元素的新数组为[0,0,0,2] 3.代码： class Solution:"""@param: A: A list of integers@pa
Leetcode#172. Factorial Trailing Zeroes
题目描述：给定一个整数 n，计算 n! 末尾有多少个0 解题思路：虽然代码只有短短几行，但问题的解决是需要技巧的。 首先明确一个问题，n! 末尾若有0出现，那么一定是 2 * 5得来的，所以如果我们知道了 n! 中有多少个 2 * 5，那么就知道了末尾有多少个0；接下来，我们就想一想n! 中有多少个 2 * 5？有一个事实，在 n! 中，2的个数一定是大于5的个数的，有博主给出了证明，如下：
172.【2023年华为OD机试真题（C卷）】围棋的气（深度优先搜索DFS实现JavaPythonC++）
🚀你的旅程将在这里启航！本专栏所有题目均包含优质解题思路，高质量解题代码，详细代码讲解，助你深入学习，深度掌握！ 文章目录 【华为OD机试AB必刷题目】题目描述解题思路 题解代码Python题解代码JAVA题解代码C/C++题解代码代码OJ评判结果 代码讲解Python题解代码讲解JAVA题解代码讲解C/C++题解代码讲解寄语
curl: 源代码从 300 行到 172,000 行，它用了 23 年
源代码从 300 行到 172,000 行，它用了 23 年 【CSDN 编者按】历经 197 次版本更新，源码从 1996 年的 300 行到如今的 172,000 行，月下载量高达 15,600 GB，支持 26 种传输协议……cURL 作者 Daniel Stenberg 在个人网站回顾了该项目历史。 作者 | Daniel Stenberg 译者 | 弯月 出品 | CSD
【优化求解】基于matlab遗传算法求解岛屿物资补给优化问题【含Matlab源码 172期】
✅博主简介：热爱科研的Matlab仿真开发者，修心和技术同步精进，Matlab项目合作可私信。 🍎个人主页：海神之光 🏆代码获取方式： 海神之光Matlab王者学习之路—代码获取方式 ⛳️座右铭：行百里者，半于九十。 更多Matlab仿真内容点击👇 Matlab图像处理（进阶版） 路径规划（Matlab） 神经网络预测与分类（Matlab） 优化求解（Matlab） 语音处理（Matlab