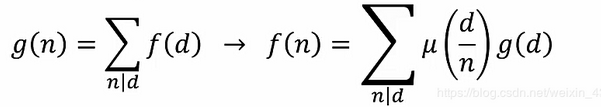Frogs' Neighborhood Time Limit: 5000MS Memory Limit: 10000KTotal Submissions: 6397 Accepted: 2793 Special Judge Description 未名湖附近共有N个大小湖泊L1, L2, ..., Ln(其中包括未名湖)，每个湖泊Li里住着一只青蛙Fi(1 ≤ i ≤ N

Frogs' Neighborhood Time Limit: 5000MS Memory Limit: 10000KTotal Submissions: 6062 Accepted: 2629 Special Judge Description 未名湖附近共有N个大小湖泊L1, L2, ..., Ln(其中包括未名湖)，每个湖泊Li里住着一只青蛙Fi(1 ≤ i ≤ N

URL: http://poj.org/problem?id=1659 Description 未名湖附近共有N个大小湖泊L1, L2, ..., Ln(其中包括未名湖)，每个湖泊Li里住着一只青蛙Fi(1 ≤ i ≤ N)。如果湖泊Li和Lj之间有水路相连，则青蛙Fi和Fj互称为邻居。现在已知每只青蛙的邻居数目x1, x2, ..., xn，请你给出每两个湖泊之间的相连关系。 Inp

✅博主简介：热爱科研的Matlab仿真开发者，修心和技术同步精进，Matlab项目合作可私信。 🍎个人主页：海神之光 🏆代码获取方式： 海神之光Matlab王者学习之路—代码获取方式 ⛳️座右铭：行百里者，半于九十。 更多Matlab仿真内容点击👇 Matlab图像处理（进阶版） 路径规划（Matlab） 神经网络预测与分类（Matlab） 优化求解（Matlab） 语音处理（Matlab

这里是原题地址：Frogs' Neighborhood         算法的在我的另一篇博文里讲的比较清楚了Havel–Hakimi algorithm         这里直接贴代码，是用stl优先队列实现的，内存消耗比较大 /*****************************************************************> File Name: P

前置知识点:click具体一些简单的证明可以自己证明一下。 具体的各项知识以及证明待更吧。。。。 题目：click 题意：给出a,b,c,d,k,求出a<=x<=b, c<=y<=d 且gcd(x,y) = k 的（x,y）的对数。 说明了(5,7)和(7,5)是同一对。可以把a，c看作是1。 思路： 由上述公式，先进行分析，线性筛选求莫比乌斯函数可以直接看代码，也比较好理解。 gcd(x,y

Frogs' Neighborhood Time Limit: 5000MS Memory Limit: 10000KTotal Submissions: 5819 Accepted: 2498 Special Judge Description 未名湖附近共有N个大小湖泊L1, L2, ..., Ln(其中包括未名湖)，每个湖泊Li里住着一只青蛙Fi(1 ≤ i ≤ N)。如果湖泊L

这里是原题地址：Frogs' Neighborhood         算法的在我的另一篇博文里讲的比较清楚了Havel–Hakimi algorithm         这里直接贴代码，是用stl优先队列实现的，内存消耗比较大 /*****************************************************************> File Name: P

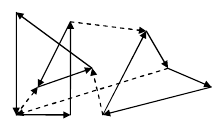
传送门：UVa 1659 Help Little Laura 题目大意：平面上有m条有向线段连接了n个点。你从某个点出发顺着有向线段行走，给走过的每条线段涂一种不同的颜色，最后回到起点。你可以多次行走，给多个回路涂色（要么不涂色，要么就至少给一个回路上的边全部涂色）。可以重复经过一个点，但不能重复经过一条有向线段。如下图所示的是一种涂色方法（虚线表示未涂色）。 每涂一个单位长度将得到X分，

给定一个非负整数序列{dn}，若存在一个无向图使得图中各点的度与此序列一一对应，则称此序列可图化。进一步，若图为简单图，则称此序列可简单图化。 可图化的判定：d1+d2+……dn=0（mod 2）。关于具体图的构造，我们可以简单地把奇数度的点配对，剩下的全部搞成自环。 可简单图化的判定（Havel定理）：把序列排成不增序，即d1>=d2>=……>=dn，则d可简单图化当且仅