UVa 1659 Help Little Laura 最大费用循环流

传送门：UVa 1659 Help Little Laura

题目大意：平面上有m条有向线段连接了n个点。你从某个点出发顺着有向线段行走，给走过的每条线段涂一种不同的颜色，最后回到起点。你可以多次行走，给多个回路涂色（要么不涂色，要么就至少给一个回路上的边全部涂色）。可以重复经过一个点，但不能重复经过一条有向线段。如下图所示的是一种涂色方法（虚线表示未涂色）。

每涂一个单位长度将得到X分，但每使用一种颜色将扣掉Y分。假设你拥有无限多种的颜色，问如何涂色才能使得分最大？输入保证若存在有向线段u -> v，则不会出现有向线段v -> u。n <= 100，m <= 500，1 <= X，Y <= 1000。

对于坐标（x，y）0 <= x，y <= 1000。

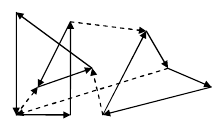
本题的模型是：给出一张有向图，从中选出权和最大的边集，组成若干个有向圈。这里的边权等于题目中的d*X - Y，其中d为边的两个端点的欧几里德距离。

本题就是最大费用循环流问题。

先给代码。。。

代码如下：

#include <stdio.h>
#include <string.h>
#include <math.h>
#include <algorithm>
#define clear(A, X) memset(A, X, sizeof A)
#define min(A, B) ((A) < (B) ? (A) : (B))
using namespace std;const int maxE = 2000000;
const int maxN = 256;
const int maxM = 32;
const double eps = 1e-8;
const int oo = 0x3f3f3f3f;struct Edge {int v, c, n;double w;
};Edge edge[maxE];
int adj[maxN], cntE;
int Q[maxE], head, tail;
int inq[maxN], cur[maxN], f[maxN];
double d[maxN];
int flow, s, t;
double cost;
int N, X, Y;
int x[maxN], y[maxN];
int deg[maxN];
int G[maxN][maxN];
double porfit[maxN][maxN];void addedge (int u, int v, int c, double w) {edge[cntE].v = v;edge[cntE].c = c;edge[cntE].w = w;edge[cntE].n = adj[u];adj[u] = cntE++;edge[cntE].v = u;edge[cntE].c = 0;edge[cntE].w = -w;edge[cntE].n = adj[v];adj[v] = cntE++;
}int spfa () {f[s] = oo;for (int i = 0; i < maxN; ++ i) d[i] = oo;clear (inq, 0);head = tail = 0;d[s] = 0;Q[tail ++] = s;cur[s] = -1;while (head != tail) {int u = Q[head ++];inq[u] = 0;for (int i = adj[u]; ~i; i = edge[i].n) {int v = edge[i].v;if (edge[i].c && d[v] > d[u] + edge[i].w) {d[v] = d[u] + edge[i].w;f[v] = min (f[u], edge[i].c);cur[v] = i;if (!inq[v]) {Q[tail ++] = v;inq[v] = 1;}}}}if (d[t] == oo) return 0;flow += f[t];cost += d[t] * f[t];for (int i = cur[t]; ~i; i = cur[edge[i ^ 1].v]) {edge[i].c -= f[t];edge[i ^ 1].c += f[t];}return 1;
}double MCMF () {flow = cost = 0;while (spfa ());return cost;
}void init () {clear (adj, -1);cntE = 0;
}double dist (int i, int j) {return sqrt ((double) (x[i] - x[j]) * (x[i] - x[j]) + (y[i] - y[j]) * (y[i] - y[j]));
}void work () {int number;double sum = 0;init ();clear (deg, 0);clear (G, 0);s = 0; t = N + 1;scanf ("%d%d", &X, &Y);for (int i = 1; i <= N; ++ i) {scanf ("%d%d", &x[i], &y[i]);while (1) {scanf ("%d", &number);if (!number) break;G[i][number] = 1;}}for (int i = 1; i <= N; ++ i) {for (int j = 1; j <= N; ++ j) {if (G[i][j]) {porfit[i][j] = Y - dist (i, j) * X;if (porfit[i][j] > 0) {addedge (i, j, 1, porfit[i][j]);}else {addedge (j, i, 1, -porfit[i][j]);//deg[] < 0：出度小于入度，deg[] > 0：出度大于入度++deg[j];--deg[i];sum += porfit[i][j];}}}}for (int i = 1; i <= N; ++ i) {if (deg[i] > 0) addedge (s, i,  deg[i], 0);if (deg[i] < 0) addedge (i, t,  -deg[i], 0);}printf ("%.2f\n", -(MCMF () + sum) + eps);
}int main () {int cas = 0;while (~scanf ("%d", &N) && N) printf ("Case %d: ", ++cas), work ();return 0;
}