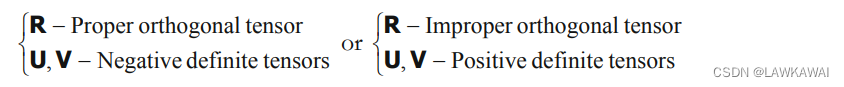涉及积分的定理 分部积分 分部积分： ∫ a b u ( x ) v ′ ( x ) d x = u ( x ) v ( x ) ∣ a b − ∫ a b v ( x ) u ′ ( x ) d x \int_a^bu(x)v'(x)dx=u(x)v(x)|_a^b-\int_a^bv(x)u'(x)dx ∫ab​u(x)v′(x)dx=u(x)v(x)∣ab​−∫ab​v(x)u′(x)

张量的范数 张量的大小，使用Frobenius 范数： ∣ ∣ v ⃗ ∣ ∣ = v ⃗ ⋅ v ⃗ = v i v i （向量） ||\vec v|| = \sqrt{\vec v \cdot \vec v} = \sqrt{v_iv_i} （向量） ∣∣v ∣∣=v ⋅v ​=vi​vi​ ​（向量） ∣ ∣ T ∣ ∣ = T : T = T i j T i j