裂开专题
单细胞核转录组——植物:叶叶我呀裂开啦~
单细胞转录组测序技术能够在单细胞分辨率下研究样本的转录组信息,可以完美解决细胞异质问题,能全面真实揭示细胞多样性和复杂性,能够更加深入地研究细胞类型、细胞功能、细胞亚群及其异质性、细胞谱系等,还常用于识别新的细胞类型、确认罕见的细胞群、构建细胞状态和系统发育的图谱。目前单细胞转录组测序技术大多应用在生物医学领域,随着单细胞转录组测序技术的发展,点燃了单细胞测序技术在植物学领域的研究热潮。凌恩生物特
语雀宕机整整8个小时,数字花园裂开了
昨天10月23日14点到22点半,凉了8小时有余 这故障时长,放眼整个互联网也是炸裂般的存在 要是再晚个半小时修复,差点连 3 个 9 的(99.9%)可用性都保证不了 3个9可用性是用来衡量系统的可用性 目前,业界衡量系统可用性的方式主要有2种: 时间纬度的系统可用性。请求纬度的系统可用性。 上述两个可用性的计算方式为: 时间纬度的系统可用性: Availability
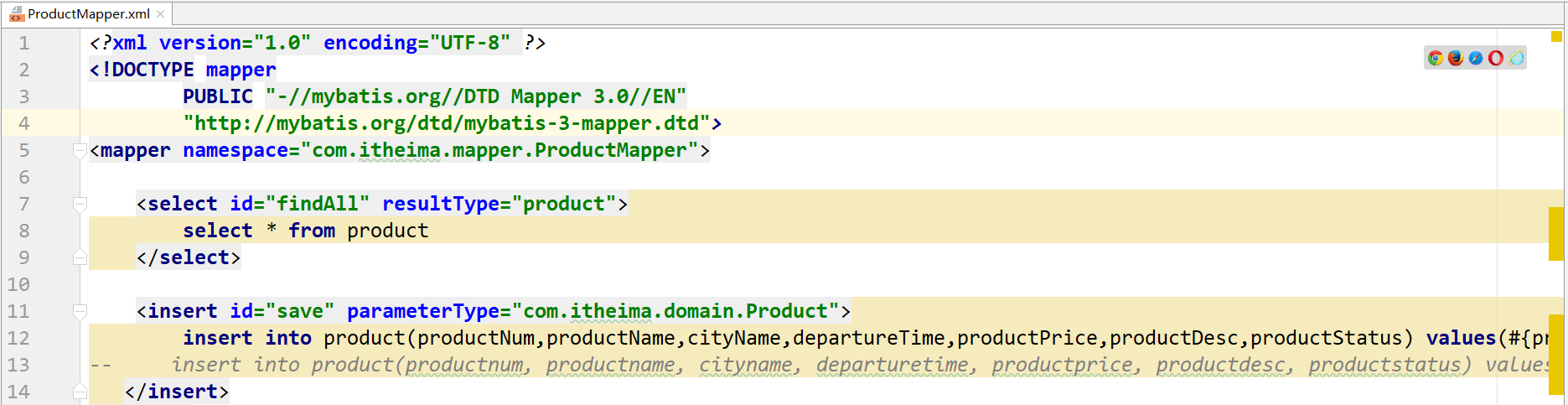
java执行sql文件有注释,这个坑,我裂开了!!!mybatis的mapper.xml文件中sql语句前后有注释掉的sql都会报错,那注释这个功能在这还有毛用???/捂脸/捂脸......
Request processing failed; nested exception is org.mybatis.spring.MyBatisSystemException: nested exception is org.apache.ibatis.type.TypeException: Could not set parameters for mapping: ParameterMapp
关于修改数据库服务器时间导致达梦数据库集群裂开
故障原因: 因为每天数据库服务器时间都不一致,想要给数据库服务器配置个NTP服务器。结果导致达梦数据库裂库。后面查看了达梦系统管理员手册了解了达梦集群的机制,知道数据库服务器时间需要先关闭数据库服务之后才可以修改数据库服务器时间。 现在只能恢复数据库集群了。 数据库模式是读写分离:1主库,N备库 监听器IP是:192.168.1.199 主库IP是:192.168.1.206 备库1IP是:1
知乎热议:拿爱因斯坦相对论证明勾股定理,网友:我裂开了
公众号关注 “GitHubDaily” 设为 “星标”,带你了解技术圈内新鲜事! 相对论也没想到,自己有生之年还可以被拿来证明勾股定理。 勾股定理是什么,人人都知道: 在平面上的一个直角三角形中,两个直角边边长的平方加起来等于斜边长的平方。 如果设直角三角形的两条直角边长度分别是 a 和 b,斜边长度是 c,那么可以用数学语言表达为「a²+b²=c²」。 勾股定理是数学定理中证明方法最多
接手了一个外包开发的项目,我感觉我的头快要裂开了~
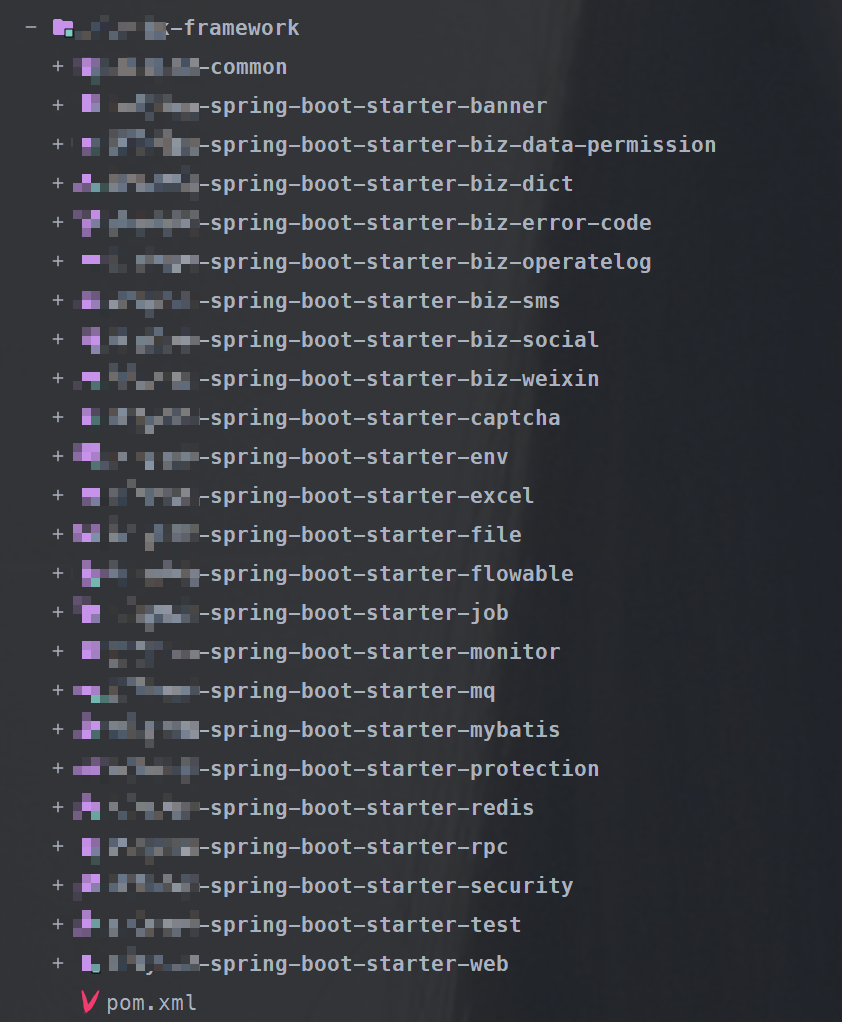
嗨,大家好,我是飘渺。 最近,我和小伙伴一起接手了一个由外包团队开发的微服务项目,这个项目采用了当前流行的Spring Cloud Alibaba微服务架构,并且是基于一个“大名鼎鼎”的微服务开源脚手架(附带着模块代码截图,相信很多同学一看就能认出来)。然而,在这段时间里,我受到了来自"外包"和"微服务"这双重debuff的折磨。 今天,我想和大家分享一下我在这几天中遇到的问题。希望这几个
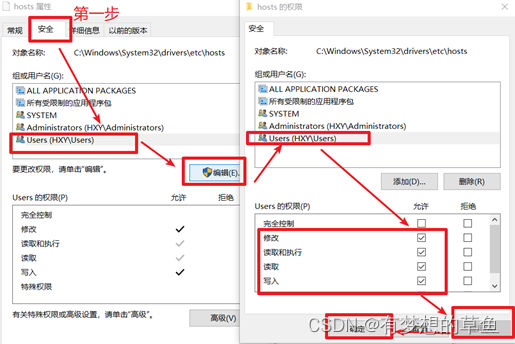
解决github图片裂开的问题,以及修改host文件的权限
解决github图片裂开的问题 在Typora中的图片采用上传到github上保存的方式,但是发现图片加载失败,图裂开了 下载图片试一试,结果是如下画面 解决方法如下: 1、 先用https://site.ip138.com/raw.githubusercontent.com/ 对ip进行查询 2、 然后把第一条的ip+raw.githubusercontent.com复制到host文
语雀宕机整整8个小时,数字花园裂开了
昨天10月23日14点到22点半,凉了8小时有余 这故障时长,放眼整个互联网也是炸裂般的存在 要是再晚个半小时修复,差点连 3 个 9 的(99.9%)可用性都保证不了 3个9可用性是用来衡量系统的可用性 目前,业界衡量系统可用性的方式主要有2种: 时间纬度的系统可用性。请求纬度的系统可用性。 上述两个可用性的计算方式为: 时间纬度的系统可用性: Availability
爱因斯坦相对论证明勾股定理,人教版数学教材引围观,网友:我裂开了
点击上方“3D视觉工坊”,选择“星标” 干货第一时间送达 相对论也没想到,自己有生之年还可以被拿来证明勾股定理。 勾股定理是什么,人人都知道: 在平面上的一个直角三角形中,两个直角边边长的平方加起来等于斜边长的平方。 如果设直角三角形的两条直角边长度分别是 a 和 b,斜边长度是 c,那么可以用数学语言表达为「a²+b²=c²」。 勾股定理是数学定理中证明方法最多的定理之一,现存几百种