线代中其他的一些遗留小问题，后续可能会更新。 1. 初等行变换不改变什么？（初等列变换同理） 初等行变换不改变列向量的线性相关性，也不改变行向量的线性相关性。可从以下两点来看。 ① 初等变换不改变矩阵的秩，矩阵的秩=列秩=行秩。而相关性就体现为是否满秩。 ② 不改变列向量的相关性，是因为初等行变换的过程始终保持了与原方程组同解，所以列向量间的线性关系（就是系数x1，x2……的取值，就

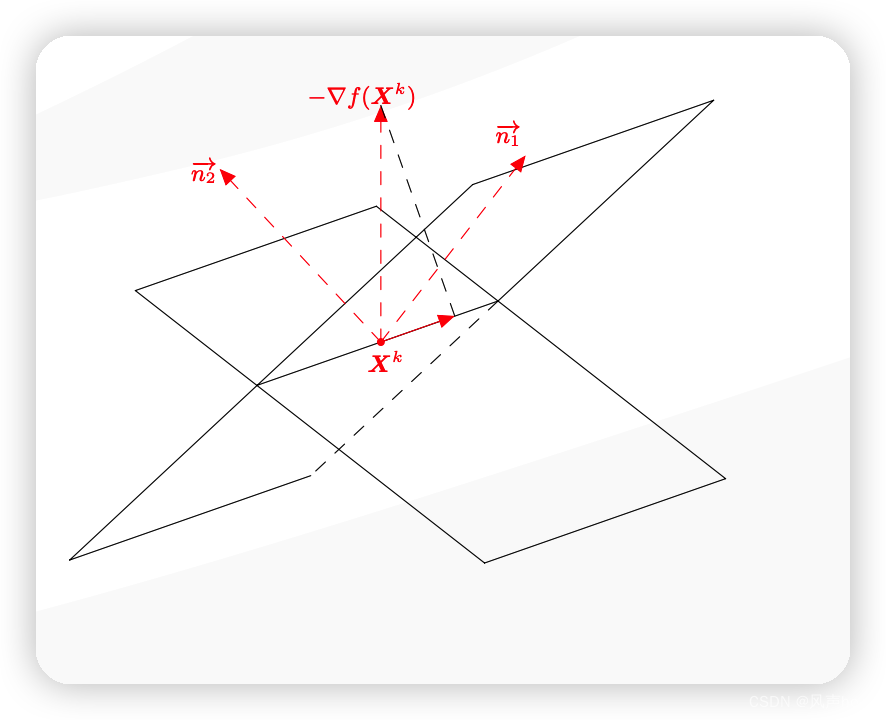
向量投影：如何将一个向量投影到矩阵的行向量生成子空间？ 前言 本问题是在学习Rosen梯度投影优化方法的时候遇到的问题，主要是对于正交投影矩阵(NT(NNT)-1N)的不理解，因此经过查阅资料，学习了关于向量投影的知识，记录如下。 首先需要了解 子空间和子空间的正交补。相关知识可以查阅本人的另外一篇笔记，核和值域的关系：什么是矩阵的秩？，这篇笔记中是以矩阵列向量的生成子空间为例展开的。 核

向量投影：如何将一个向量投影到矩阵的行向量生成子空间？ 前言 本问题是在学习Rosen梯度投影优化方法的时候遇到的问题，主要是对于正交投影矩阵(NT(NNT)-1N)的不理解，因此经过查阅资料，学习了关于向量投影的知识，记录如下。 首先需要了解 子空间和子空间的正交补。相关知识可以查阅本人的另外一篇笔记，核和值域的关系：什么是矩阵的秩？，这篇笔记中是以矩阵列向量的生成子空间为例展开的。 核