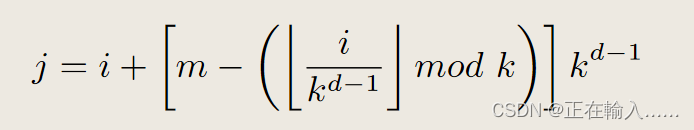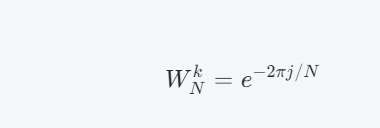蝶形专题
【Interconnection Networks 互连网络】Flattened Butterfly 扁平蝶形拓扑
Flattened Butterfly 扁平蝶形拓扑 1. 传统蝶形网络 Butterfly Topology2. 扁平蝶形拓扑 Flattened Butterfly3.On-Chip Flattened Butterfly 扁平蝶形拓扑应用于片上网络 Flattened Butterfly 扁平蝶形拓扑 扁平蝶形拓扑是一种经济高效的拓扑,适用于高基数路由器。扁平蝶形是通过组合(或扁平化)
Flattened Butterfly 扁平蝶形拓扑
Flattened Butterfly 扁平蝶形拓扑 1. 传统蝶形网络 Butterfly Topology2. 扁平蝶形拓扑 Flattened Butterfly3.On-Chip Flattened Butterfly 扁平蝶形拓扑应用于片上网络 Flattened Butterfly 扁平蝶形拓扑 扁平蝶形拓扑是一种经济高效的拓扑,适用于高基数路由器。扁平蝶形是通过组合(或扁平化)
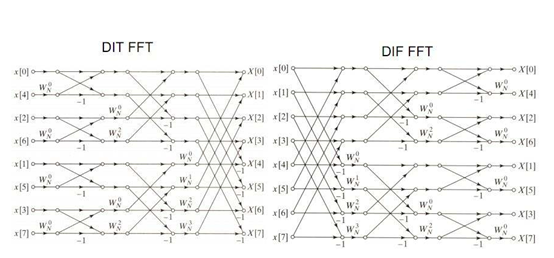
matlab 8点fft蝶形图,基2时抽8点FFT的matlab实现流程及FFT的内部机理
前言 本来想用verilog描述FFT算法,虽然是8点的FFT算法,但写出来的资源用量及时延也不比调用FFT IP的好, 还是老实调IP吧,了解内部机理即可,无需重复发明轮子。 参考 流程 FFT能做什么在此就不赘述了,只了解数据的运算流程。 1.FFT的基本公式: 第一眼看这个公式,肯定是脑袋瞬间宕机。 2.旋转因子:记住旋转因子具有可约性,对称性,周期性。 表示方法有两种,通过欧拉公式转换