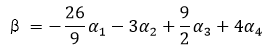相关性分析（具体来说，皮尔逊成对相关性）和回归分析（具体来说，双变量最小二乘 (OLS) 回归）具有许多共同的特征： 两者都定期应用于两个连续变量（我们称之为 X 和 Y）。通常向学生介绍这两种图表时使用的是同一类型的图表：散点图。二者从根本上讲都是关于 X 中的偏差（即相对于平均值的单个值）与 Y 中的偏差之间的关系。两者都假设 X 和 Y 之间存在线性关系。两者都可以用于经典的假设检验，每个

线性表出、线性相关的定理总结思考 1.n维向量组 α1,α2,α3,...,αs \alpha_1,\alpha_2,\alpha_3,...,\alpha_s线性相关， ⟺ \Longleftrightarrow齐次方程组 (α1,α2,α3,...,αs)⋅⎡⎣⎢⎢⎢⎢⎢⎢⎢x1x2...xs⎤

线性模型内容 引言 真实数据集中不同维度的数据通常具有高度的相关性，这是因为不同的属性往往是由相同的基础过程以密切相关的方式产生的。在古典统计学中，这被称为——回归建模，一种参数化的相关性分析。   一类相关性分析试图通过其他变量预测单独的属性值，另一类方法用一些潜在变量来代表整个数据。前者的代表是 线性回归，后者一个典型的例子是 主成分分析。本文将会用这两种典型的线性相关分析方法进行异常检测

向量组 向量组：有限个相同维度的行向量或列向量组合成的一个集合就叫做向量组A 如果是行向量，那么表示为： A = ( a 1 ⃗ a 2 ⃗

这一篇文章和大家聊聊向量。 向量与平面 向量这个概念我们在高中就接触到了，它既指一个点在空间中的坐标，也表示一个有向线段，如果我们加入复数概念的话，它还能表示一个数。在线性代数当中，向量就是指的n个有次序的数 a 1 , a 2 , ⋯ , a n a_1, a_2, \cdots, a_n a1​,a2​,⋯,an​组成的数组。 向量可以写成一行，也可以写成一列。写成一列的称为列向

线性代数之线性相关线性表示的求法 线性相关 向量是n个m维(每个向量分量的个数)的向量，若存在一组不全为0的    使得 则 是线性相关的，反之线性无关。  线性无关即等价于以下命题： 线性不相关找不到一组不全0的   使得  全为0 几种情况: 关于单个向量 向量组中两个向量成比例，则两个向量必线性相关含零向量的任向量组必线性相关(取0向量的系数为1或者k，其余均为0)一个

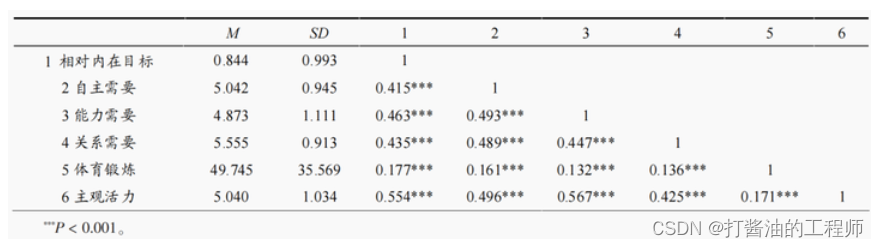
目录 学习目的软件版本原始文档线性相关分析0 引言1. 绘制散点图2.计算r系数一、实战案例二、统计策略统计分析步骤：三、SPSS操作1、正态性检验2、绘制散点图3、正式分析 四、结果解读五、规范表达1、规范图表2、规范文字 六、划重点 学习目的 SPSS第十八讲：如何进行线性相关分析？ 软件版本 IBM SPSS Statistics 26。 原始文档 《小白爱上SP

标签 PostgreSQL , 文本相似性分析 , tf , idf , tf-idf , tag , 相关性 , 余弦相关性 , 线性相关性 , 关键词 , tfidf向量 , rum , smlar , cosine 背景 前面介绍了tf-idf算法，以及它在文本分析中的应用(提取关键词)，参考如下。 《文本(关键词)分析 - TF(Term Frequency 词频) IDF(Inve