相除专题
一个google的面试题 计算两个整数相除
Divide number and return result in form of a string. e.g 100/3 result should be 33.(3) Here 3 is in brackets because it gets repeated continuously and 5/10 should be 0.5. 这题难在怎么去判断循环和记录循环出现的位置 上代码:
两个long型数据相除结果错误问题解决
long A=1; long B=2; 因为两个long型数据相除默认取整数,所以就有 A/B=0; 这样的结果是不准确的,我们可以通过将被除数乘以1.0,这时的结果就会带小数了 A*1.0/B=0.5 当我们用两个long型计算文件的下载百分比的时候,可以将被除数先乘以100,这样得到的就直接是百分数了。 A*100/B
verilog中两个常数相除
在Verilog中,两个常数(即编译时已知的值)相除,其结果的处理方式取决于几个因素,包括这些常数的类型(整数还是实数)、Verilog的版本(Verilog-2001之前的版本与SystemVerilog有所不同,尽管后者在很大程度上与Verilog兼容并扩展了其功能),以及你期望的结果类型。 整数除整数 如果两个操作数都是整数,那么结果也将是整数,并且结果会向下取整(即,丢弃小数部分)。这
java求两个整数相除得到的小数
在 Java 中,进行整数相除操作时,如果操作数都是整数,结果也会是整数,并且小数部分会被丢弃。如果你希望得到一个包含小数部分的结果,你需要将其中至少一个操作数转换为浮点类型(如 double 或 float)。 类型转换 public class DivisionExample {public static void main(String[] args) {int numerator =
数论基础 辗转相除 扩展欧几里德
辗转相除: 辗转相除,又称为欧几里德算法,用于求解俩个数值的最大公约数,原理如下: gcd(a,b) = gcd(b,a%b) = gcd(a%b,(a%b)%b) ... = gcd(c,0) = c; 一般经过俩次的递归之后,第一个参数就小于原来的一半,所以不用但是栈溢出的情况。 int gcd(int a,int b){if(b==0)return a;return
【Leetcode 29】 两数相除
题目描述 方法一: 题干中说明不能用乘法和除法, 那么我们可以用减法, 被除数最多可以减多少个除数还能保证是非负的即可.换句话说商为被除数减去除数的总次数 class Solution:def divide(self, dividend, divisor):sig = True if dividend*divisor > 0 else False # 判断二者相除是正or负dividend
1016 两浮点数相除
#include<iostream>#include<iomanip>using namespace std;int main(){double a,b,c;cin>>a>>b;c=a/b;cout<<setiosflags(ios::fixed)<<setprecision(2)<<c<<endl;return 0;}
浅谈一下大数相除有关思路(图解)与用java代码具体解决方案
浅谈一下大数相除有关思路(图解)与用java代码具体解决方案 PS:接上篇大数相乘博客。两数的正负情况在这就不谈了,只要加一个标记就可以了。此文阅读前提:需在解决了大数相加减和大数相乘的基础上进行。 在完成了大数相乘的程序后,很自然地想到了在不使用java API的情况下,如何实现两个数相除,两数可以是大数和小数的任意组合,如大数/大数,大数/小数。 思路图解1
LintCode_两个整数相除
问题描述: 将两个整数相除,要求不使用乘法、除法和 mod 运算符。如果溢出,返回 2147483647 。 样例:给定被除数 = 100 ,除数 = 9,返回 11。 算法思想: 方法一:(这是开始自己想出来的,算法思想简单,缺点是,循环次数多,运行速度慢) 如果不能采用乘除运算方法,那么可以采用加减方式,当然还要(1)、注意分类:正正,正负,负正,负负;(2)、溢出问题;
2024/4/1—力扣—两数相除
代码实现: 思路:用减法模拟除法 // 用减法模拟除法int func(int a, int b) { // a、b均为负数int ans = 0;while (a <= b) { // a的绝对值大于等于b,表示此时a够减int t = b;int count = 1; // 用来计数被减的次数// t >= INT_MIN / 2:防止减数越界,并且保证a的绝对值比两倍减数的
1029:计算浮点数相除的余--信息学一本通(c++)
NOIP信息学奥赛资料下载 时间限制: 1000 ms 内存限制: 65536 KB 提交数: 19181 通过数: 11422 【题目描述】 计算两个双精度浮点数a和b的相除的余数,a和b都是双精度浮点数。这里余数(r)的定义是:a=k×b+r,其中k是整数,0≤r<b。 【输入】 输入仅一行,包括两个双精度浮点数a和b。 【输出】 输出也仅一行,a÷b的余数。 【输入样例】 73.263
android 两数相除,保留两位及多位小数
/*** valueOne:除数* valueTwo:被除数* scale:保留几位小数*/fun divide(valueOne: Int, valueTwo: Int, scale: Int): Double {if (scale < 0) {throw IllegalArgumentException("The scale must be a positive integer or zero
c++计算浮点数相除的余
题目描述 计算两个双精度浮点数a和b的相除的余数,a 和 b 都是双精度浮点数。这里余数(r)的定义是:a=k×b+r,其中k是整数,及 k=a/b,0<=r<b 输入描述 输入仅一行,包括两个双精度浮点数 a 和 b。 输出描述 输出也仅一行,a÷b的余数。 样例输入 1 73.263 0.9973 样例输出 1 0.4601 #include <bits
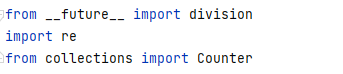
python整数相除保留小数SyntaxError: from __future__ imports must occur at the beginning of the file
原文地址:https://program-park.github.io/2021/08/23/python_13/ 今天在测试时发现结果有问题,排查出是因为两个变量相除时没有保留小数 通过百度可以通过添加from __future__ import division的方法来保留小数,结果运行后报下面的错 最后发现原来from __future__ import division是要放在
C语言疑难题:杨辉三角形、辗转相除求最大公约数、求π的近似值、兔子问题、打印菱形
杨辉三角形:打印杨辉三角形的前10行 /* 杨辉三角形:打印杨辉三角形的前10行 */ #include<stdio.h> int main(){ int i,j; int a[10][10]; printf("\n"); for(i=0;i<10;i++){ a[i][0]=1; a[i][i]=1; }
mysql 通过子查询实现两列相除
摘要:催收系统中有个根据前一天催收回单率排序的sql,其中:前一天催收回单率=前一天催收回单量/前一天的全部回单量,下面是对应的SQL语句: 一:查询前一天的回单量: SELECTcount(1) AS '前一天回单量'FROMcui_task tWHEREDATE_FORMAT(t.assignDate, '%Y-%m-%d') = date_sub(curdate(), INTE
代码随想录算法训练营番外 刷题日记0301 || 29、两数相除,31、下一个排列
29、两数相除 思路:不断相减就是求解的最直接方法,我这样计算时间复杂度有点高 // 时间复杂度O(count*divisor)// 空间复杂度O(1)class Solution {int res = 0;public int divide(int dividend, int divisor) {// dividend 是被除数if(dividend == 0) return 0;if
Leetcode29:两数相除
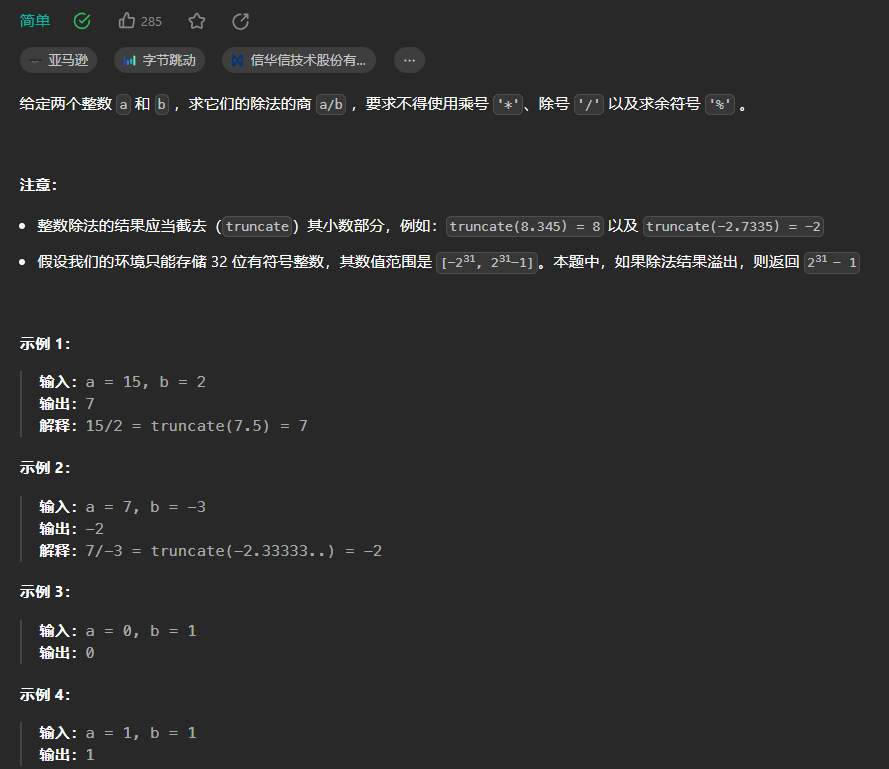
一、题目描述 给你两个整数,被除数 dividend 和除数 divisor。将两数相除,要求 不使用 乘法、除法和取余运算。 整数除法应该向零截断,也就是截去(truncate)其小数部分。例如,8.345 将被截断为 8 ,-2.7335 将被截断至 -2 。 返回被除数 dividend 除以除数 divisor 得到的 商 。 注意:假设我们的环境只能存储 32 位 有符号整数,其数值
Leetcode—29. 两数相除【中等】
2023每日刷题(九十四) Leetcode—29. 两数相除 叛逆期实现代码 class Solution {public:int divide(int dividend, int divisor) {if(dividend == INT_MIN && divisor == -1) {return INT_MAX;} return dividend / divisor;}};
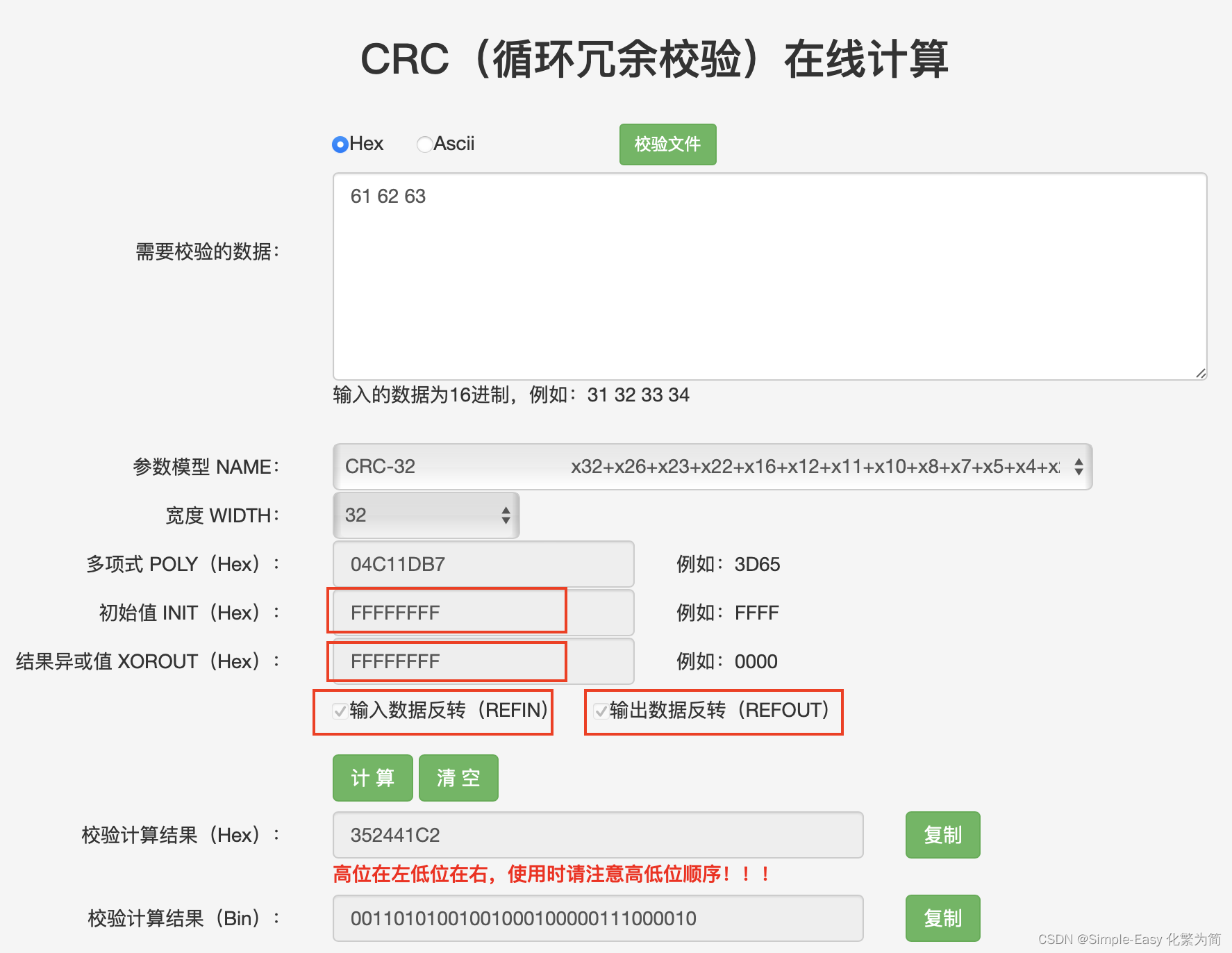
CRC32的原理介绍以及查表法实现和多项式相除实现
1、CRC32的生成多项式 多项式系数提取出来,改写位16进制数为:0x104C11DB7,如果转换为33个二进制数[1, 0, 0, 0, 0, 0, 1, 0, 0, 1, 1, 0, 0, 0, 0, 0, 1, 0, 0, 0, 1, 1, 1, 0, 1, 1, 0, 1, 1, 0, 1, 1, 1] ,那么从左到右对应于生成多项式的每个项目的系数(0或1)。
C++面试宝典第12题:数组元素相除
题目 从控制台输入若干个整数作为数组,将数组中每一个元素除以第一个元素的结果,作为新的数组元素值。比如:可以先输入3,作为数组元素的个数;然后输入3个整数,作为数组元素的值。 解析 这道题本身并不复杂,但里面隐藏了不少“坑点”和“雷区”,主要考察应聘者全面思考问题的能力。 一些应聘者咋看这道题,觉得非常简单,很快便写出了下面的示例代码
【LeetCode-剑指offer】--1.两数相除
1.两数相除 方法:使用减法实现除法 用“被减数”能减去几次“减数”来衡量最后的结果,这时候我们想到求x的幂次的快速解法,将x成倍成倍的求幂,这里将减数成倍成倍的增大,次数对应也是成倍成倍的增大,例如:取a=23,b=2,b的变化如下:2->4->8->16,次数count的变化如下1->2->4->8,最后a-b=23-16=7,对7再执行一次上述过程,b:2->4,count:1->2
老卫带你学---leetcode刷题(29. 两数相除)
29. 两数相除 问题 给你两个整数,被除数 dividend 和除数 divisor。将两数相除,要求 不使用 乘法、除法和取余运算。 整数除法应该向零截断,也就是截去(truncate)其小数部分。例如,8.345 将被截断为 8 ,-2.7335 将被截断至 -2 。 返回被除数 dividend 除以除数 divisor 得到的 商 。 注意:假设我们的环境只能存储 32 位 有
Java 两个整数int类型相除总是得0的原因及解决方法
原因: 在java中int和Integer在进行除法运算时,总是得到0,是因为整数相除后还是整数int,所以小数点后面的数都被省略掉了,只保留小数点之前的数。 解决方法: 对整数进行强制转换。 举例: public class Demo {public static void main(String[] args) {Integer a = 123;Integer b = 456;int
LeetCode——29. 两数相除
目录 题目1.链接2.题目描述3.解题思路4.题解 题目 1.链接 29. 两数相除. 2.题目描述 3.解题思路 要求商,我们首先想到的是减法,能被减多少次,那么商就为多少,但是明显减法的效率太低 那么我们可以用位移法,因为计算机在做位移时效率特别高,向左移1相当于乘以2,向右位移1相当于除以2我们可以把一个dividend(被除数)先除以2^n,n最初为3