杜利特尔分解Doolittle转化为克洛特分解Crout_解线性方程组的直接解法 标签：计算方法实验 #include <stdio.h>#include <string.h>#include <math.h>const int maxn = 15;int main(){double a[maxn][maxn], b[maxn], y[maxn], x[maxn], l[maxn][max

克洛特分解法Crout_解线性方程组的直接解法 标签：计算方法实验 #include <stdio.h>#include <math.h>const int maxn = 15;int main(){double a[maxn][maxn], b[maxn], y[maxn], x[maxn], l[maxn][maxn], u[maxn][maxn];int i, j, k, r, n,

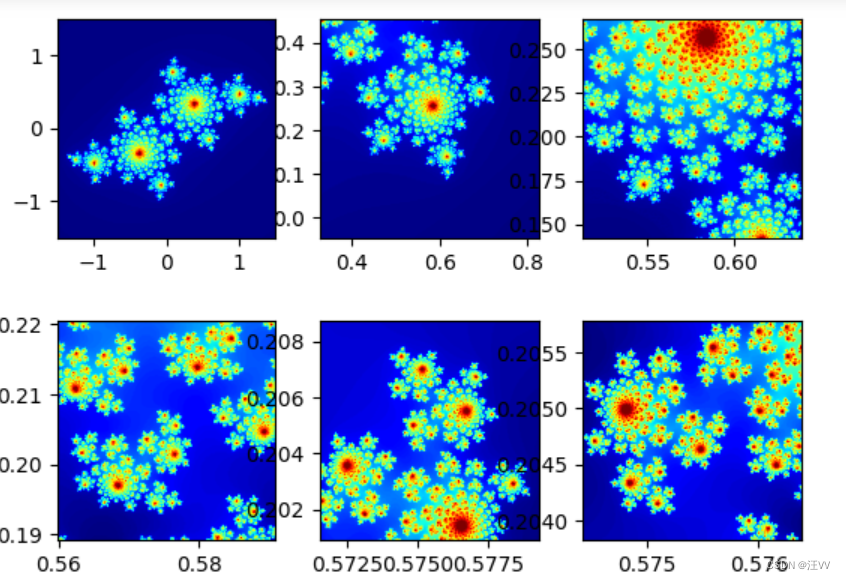
文章目录 分形的重要特征曼德布洛特集合曼德布洛特集合有一个以证明的结论：图像展示np.ogrid[]np.frompyfunc()集合转图像 julia集合 无边的奇迹源自简单规则的无限重复 ---- 分形之父Benoit B.Mandelbrot 分形的重要特征 自相似性无标度性非线性 曼德布洛特集合 z 0 = 0 z_0 = 0 z0​=0 z n + 1