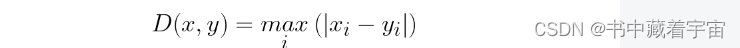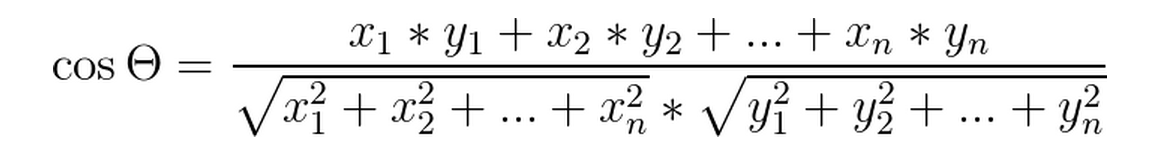在深度学习以及图像搜索中，经常要对特征值进行比对，得到特征的相似度，常见的特征值比对方法有汉明距离、余弦距离、欧式距离、曼哈顿距离、切比雪夫距离、闵可夫斯基距离、马氏距离等，下面对各种比对方法分别进行介绍。 目录 1汉明距离 2余弦相似度 3欧式距离 4曼哈顿距离 5切比雪夫距离 6闵可夫斯基距离 7马氏距离 1汉明距离 汉明距离/Hamming Distance也能用来计算两

大数定理、切比雪夫不等式及其推导 大数定律 弱大数定律（Weak Law of Large Numbers, WLLN） 弱大数定律指出，当试验次数 (n) 趋向无穷大时，样本平均值 (\bar{X_n}) 与期望值 (\mu) 之间的差异以概率收敛于0。数学上表示为： ∀ ϵ > 0 , lim ⁡ n → ∞ P ( ∣ 1 n ∑ i = 1 n X i − μ ∣ ≥ ϵ ) =

目录 一、说明 二、自然界的极限性        三、马尔可夫不等式 3.1 最早提出 3.2 马尔可夫不等式的证明 四、 Bienaymé–Chebyshev 不等式 4.1 简要回顾Bienaymé–Chebyshev 不等式的历史 4.2 Bienaymé — Chebyshev 不等式的证明 五、弱大数定律（及其证明） 5.1 定律陈述 5.2 弱大数定律的证明 一、说明

切比雪夫逼近法设计FIR滤波器 概念 切比雪夫逼近法，是在所需要的区间[a,b]内，使误差函数E(x)=|p(x)-f(x)|较均匀一致，并且通过合理选择p(x)，使E(x)的最大值En达到最小。切比雪夫最佳一致逼近的基本思想是，对于给定区间[a，b]上的连续函数f(x)，在所有n次多项式的集合中，寻找一个多项式，使其在[a，b]上对f(x)的偏差和其他一切属于集合的多项式对f(x)的偏差相比

数据间的各种距离 欧几里得距离代码 哈曼顿距离距离代码 切比雪夫距离代码 余弦距离距离代码 相关系数距离代码 马氏距离代码 数据表来源于：链接: link 欧几里得距离 代码 from scipy.spatial import distancedist1 = distance.cdist(me_data,me_data,'euclidean')print

欢迎关注更多精彩 关注我，学习常用算法与数据结构，一题多解，降维打击。 本期话题：切比雪夫（最小区域法）直线拟合算法 相关背景和理论 点击前往 主要介绍了应用背景和如何转化成线性规划问题 圆拟合输入和输出要求 输入 10到631个点，全部采样自2D圆附近。每个点3个坐标，坐标精确到小数点后面20位，最后1个坐标为0。坐标单位是mm, 范围[-500mm, 500mm]。 输出 圆

目录 1.欧式距离EuclideanDistance 2. 曼哈顿距离(ManhattanDistance) 3. 夹角余弦 4.汉明距离(Hamming Distance)     1.欧式距离EuclideanDistance 欧式距离：也称欧几里得距离，在一个N维度的空间里，求两个点的距离，这个距离肯定是一个大于等于零的数字，那么这个距离需要用两个点在各自维度上的坐标

题目大意：从给出的点中 选出一个点作为中心 ，求别的点距这个点的最小距离的和。 思路：       根据题意 可以知道 切比雪夫 d[i]=max(|xi-x|,|y-yi|),曼哈顿距离：d[i]=|y2-y1|+|x2-x1|；然后就是从切比雪夫转化曼哈顿形式，坐标逆时针旋转 45度 ，即x1=x0-y0;y1=x0+y0; 但是 因为 得出来的新坐标 扩大√2倍，那么在这个曼哈顿里 就是2

Description 有N个小松鼠，它们的家用一个点x,y表示，两个点的距离定义为：点(x,y)和它周围的8个点即上下左右四个点和对角的四个点，距离为1。现在N个松鼠要走到一个松鼠家去，求走过的最短距离。 Input 第一行给出数字N，表示有多少只小松鼠。0<=N<=10^5 下面N行，每行给出x,y表示其家的坐标。 -109<=x,y<=109 Output 表示为了聚