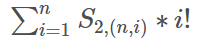UVA 10844 - Bloques 题目链接 题意：给定n个数字，问这n个数字能分成子集分成有几种分法 思路：一开始先想了个状态，dp[i][j]表示放i个数字，分成j个集合的方案，那么转移为，从dp[i - 1][j - 1]在多一个集合，和从dp[i - 1][j]有j个位置放，那么转移方程为dp[i][j] = dp[i - 1][j - 1] + dp[i - 1][j] *

第一类斯特灵数：含正负值，其绝对值是包含n个元素的集合分作k个环排列的方法数目。 递推公式   s(n,0)=0,s(1,1)=1,s(n,k)=s(n-1,k-1)+(n-1)*s(n-1,k) 第二类斯特灵数：把包含n个元素的集合划分为正好k个非空子集的方法的数目。 递推公式   s(n,k)=s(n

中国社会科学院大学-英国斯特灵大学中外合作办学创新与领导力博士DMAN项目 中国社会科学院大学-英国斯特灵大学创新与领导力博士DMAN项目是中国社会科学院大学第一个博士层次的中外合作办学项目，于2020年3月正式获得教育部批准办学，批准书编号：OE11UK1N20192019N。创新与领导力博士项目是结合理论框架及其在现实生活中的实际应用的专业博士项目，依托中国社科院及斯特灵大学丰富的学术资源，

随着在职研究生改革的不断深入，越来越多的在职人士报考在职研究生，在职博士，提升自己的学历和能力。中外合作办学博士是在职博士报考方式之一，是由国内的院校和国外院校合作开办的在职博士教育形式，分可认证和不可认证两种，那么接下来小编与中国社科院与英国斯特灵大学创新领导力博士项目与大家一起了解中外合作办学博士都能颁发什么证书。 不可认证的合作办学项目，最终只能拿到国外院校的博士学位证书，不能在教育部留学

自1978年恢复高考之后，很长一段时间里我国的高校系统处于人才很匮乏的状态，那个时候很多高校招聘了大量硕士学历教师（其中很多人在留校后又读了在职博士），而且都是事业编制。那么接下来小编与中国社科院与英国斯特灵大学创新与领导力博士同大家一起看看我们的博士之路上的重要一趴——导师。 其实无论是在学术界还是在工业界，都强调一个圈子的概念。在学术界选择导师的时候，就好比运动员选择各种各样的俱乐部，有的俱

hdu 2643 最近在Teddy的家乡举办了一场名为“Cow Year Blow Cow”的比赛.N竞争对手参加了比赛。比赛非常紧张，排名正在发生变化。 现在的问题是： 竞争者可以在竞争中排名多少种不同的方式，从而允许联系的可能性。 因为答案非常大，你可以输出答案MOD 20090126. 以下是N = 2时的方法： P1 <P2 P2 <P1 P1 = P2 输入 第一行将包含一个T，然后是

Count the Buildings 不管是从左边看还是从右边看，视线总是会被中间最高的给挡住 所以我们把左边和右边分组来看。 对于某一边，我们确定出能够看见的楼房，那么不能够看见的楼房就可以任意排列 我们把能看见的楼房，与下一个能看到的楼房（不包括下一个楼房）之间的楼看为一组 可以考虑现将最高的拿出来，那么可以考虑左边需要有F-1个房子成递增关系，那么可以将左边的房子分成F-1个组（环），

对于博士阶段来说，由于科研任务繁重，需要自主学习的内容以及接受的挑战也相对较多，所以对于晋升读博这件事并不那么容易。无论是考博还是读中外合作办学博士，上课语言、博导、论文这些关都是要一一闯过的。能遇见优秀的导师是我们的幸运！一起来看看中国社科院与英国斯特灵大学中外合作办学博士项目把！ 中国社会科学院大学（简称社科大)，英文名称University of Chinese Academy of So

对于博士阶段来说，由于科研任务繁重，需要自主学习的内容以及接受的挑战也相对较多，所以对于晋升读博这件事并不那么容易。无论是考博还是读中外合作办学博士，上课语言、博导、论文这些关都是要一一闯过的。能遇见优秀的导师是我们的幸运！一起来看看中国社科院与英国斯特灵大学中外合作办学博士项目的相关安排吧！ 2020年起，中国社会科学院大学（研究生院）与英国斯特灵大学（University of Stirli

将n个有标记的球放在m个没有标记的盒子里边，求解一共有多少放法？ 放置规则：m=0，f（m，n）=0； m=1=n，f（m，n）=1； 解题思路：考虑第m个球的方法，假如第m个球单独放置，有f（m-1，n-1）种方法； 假如第m个球与其他球在一起，有n*f（m-1，n）种放法。 放法总数：f（m，n）=f（m-1，n-1）+n*f（m-1，n）。 #include<stdio.h>