换根专题
AcWing 287. 积蓄程度(树形dp,换根+二次扫描)
有一个树形的水系,由 N-1 条河道和 N 个交叉点组成。 我们可以把交叉点看作树中的节点,编号为 1~N,河道则看作树中的无向边。 每条河道都有一个容量,连接 x 与 y 的河道的容量记为 c(x,y)。 河道中单位时间流过的水量不能超过河道的容量。 有一个节点是整个水系的发源地,可以源源不断地流出水,我们称之为源点。 除了源点之外,树中所有度数为 1 的节点都是入海口,可以吸收无限多
CF1156D 0-1-Tree 换根DP
参考 https://www.luogu.org/problemnew/solution/CF1156D D. 0-1-Tree time limit per test 2 seconds memory limit per test 256 megabytes input standard input output standard output You are given a
[洛谷-P3047] [USACO12FEB]Nearby Cows G(树形DP+换根DP)
[洛谷-P3047] [USACO12FEB]Nearby Cows G 一、问题题目描述输入格式输出格式样例 #1样例输入 #1样例输出 #1 提示 二、分析1、状态表示2、状态转移3、换根DP 三、代码 一、问题 题目描述 Farmer John has noticed that his cows often move between nearby fields. Taki
换根DP求树的重心/求最小距离和
DP过程 const int N = 1e6+7;int Size[N] // Size[i]表示以i为根的子树的结点数int dp[N] //dp[i]表示树中所有点到结点i的距离和dp[son]=dp[pos]+(Size[1]-Size[son])-Size[son];//状态转移方程 预处理 预处理出所有Size dfs 预处理出dp[1] dfs
Codeforces Round 899 (Div. 2)(C手玩? D换根dp+贪心)
A - Increasing Sequence 直接从1开始模拟就行 #include<bits/stdc++.h>using namespace std;const int N =2e5+10,mod=998244353;#define int long longtypedef long long LL;typedef pair<int, int> PII;const long
HDU多校第九场 1007 Rikka with Travels —— 树形DP + 换根
题目链接:点我啊╭(╯^╰)╮ 题目大意: 一棵无根树,定义 L ( a , b ) L(a,b) L(a,b) 为树上从 a a a 到 b b b 的路径点数 计算 p a i r s ( l 1 , l 2 ) pairs (l_1, l_2) pairs(l1,l2) , L ( a , b ) = l 1 , L ( c , d ) = l 2 L(a,
HDU多校第八场 1006 Acesrc and Travel —— 树形DP + 换根
题目链接:点我啊╭(╯^╰)╮ 题目大意: 一棵无根树,每个点有两个点权 a i a_i ai 和 b i b_i bi Z h a n g Zhang Zhang a n d and and L i u Liu Liu 轮流选, Z h a n g Zhang Zhang 选一个点可以得到 a i a_i ai L i u Liu Liu 选一个点
[LuoguP1829]Crash的文明表格(二次扫描与换根+第二类斯特林数)
Solution: 由于\[ x^m = \sum_{i=0}^m{~m~\choose i}{~x~\brace i}i! \] 将所求的式子化成这样,挖掘其性质,考虑是否能从儿子转移(或利用以求得信息)。\[ \begin{aligned} S(u) &= \sum_{i=1}^ndis(u,i)^k\\ &= \sum_{i=1}^n\sum_{j=0}^k{dis(u, i)
『树形DP·换根』Kamp
题目描述 题解 这道题 O ( n 2 ) O(n^2) O(n2)很简单,就是一个简单的有根树树形DP,即经过每一个特殊点的边权*2-根到某一个特殊点的最长链。 对于部分1,我们假设处理了 f [ x ] f[x] f[x],对于一条边 ( x , y , v ) (x,y,v) (x,y,v)来说,在一般情况下有: f [ y ] = f [ x ] f[y]=f[x] f[y]=f


![[洛谷-P3047] [USACO12FEB]Nearby Cows G(树形DP+换根DP)](https://img-blog.csdnimg.cn/5aa58266b0e548fa9ba3f5dbc44234c7.png)
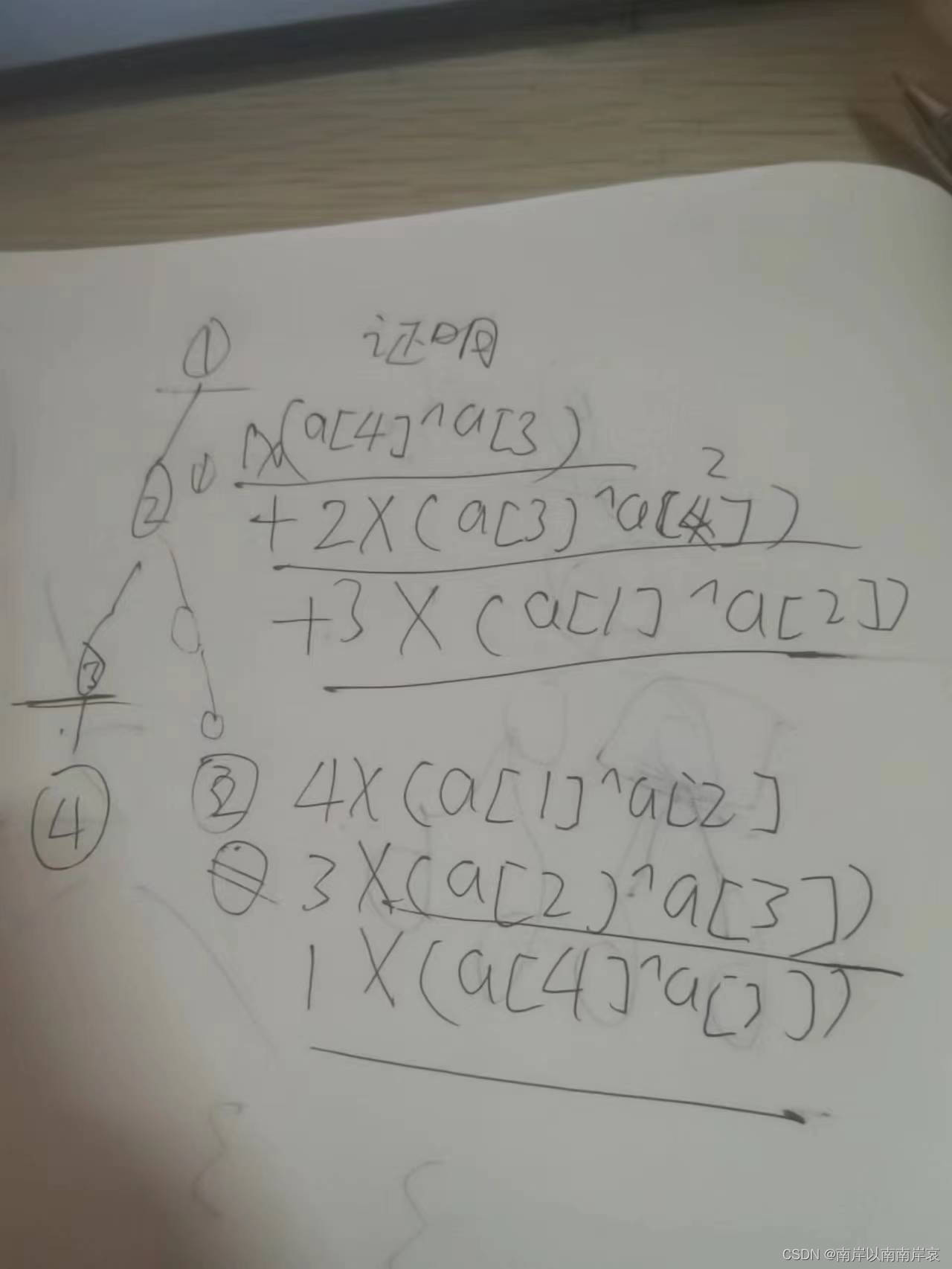
![[LuoguP1829]Crash的文明表格(二次扫描与换根+第二类斯特林数)](https://i.loli.net/2019/08/31/N6DbcXtPal7yQrB.png)
