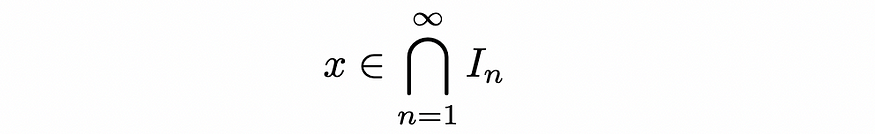我看到了它，却不敢相信它。 ——康托尔 哥德尔的不完备性定理震撼了20世纪数学界的天空，其数学意义颠覆了希尔伯特的形式化数学的宏伟计划，其哲学意义直到21世纪的今天仍然不断被延伸到各个自然学科，深刻影响着人们的思维。图灵为了解决希尔伯特著名的第十问题而提出有效计算模型，进而作出了可计算理论和现代计算机的奠基性工作，著名的停机问题给出了机械计算模型的能力极限，其深刻的意义和漂

乔治·康托尔 |图片来源： 维基百科 一、说明         对于那些对数学感兴趣的人来说，无穷大实际上可以有不同的大小，这可能是一个众所周知的事实。事实上，最著名的例子是所有实数的集合比所有自然数的集合“大”。你可能知道，这实际上有一个非常优雅的证明，称为康托尔对角线方法，由乔治·康托尔在1891年提出。如果您不知道这一点，我绝对建议您研究一下，因为我认为该方法非常聪