题目链接： 2021年的模拟赛有一道相似的题： 1.平方差 - 蓝桥云课 (lanqiao.cn) 对于这道题，一个不错的题解，证明的很清楚： 完整的请看该题题解区的第二条。 再加上每个周期第二个数不合法的证明： 用反证法： 需要证明的就是x-y=m时，m为偶数的情况，上面的证明可以证明4的倍数是合法的，但不能证明2的倍数不合法。 任意一个每个周期第二个数可以写成4n+2（n=0

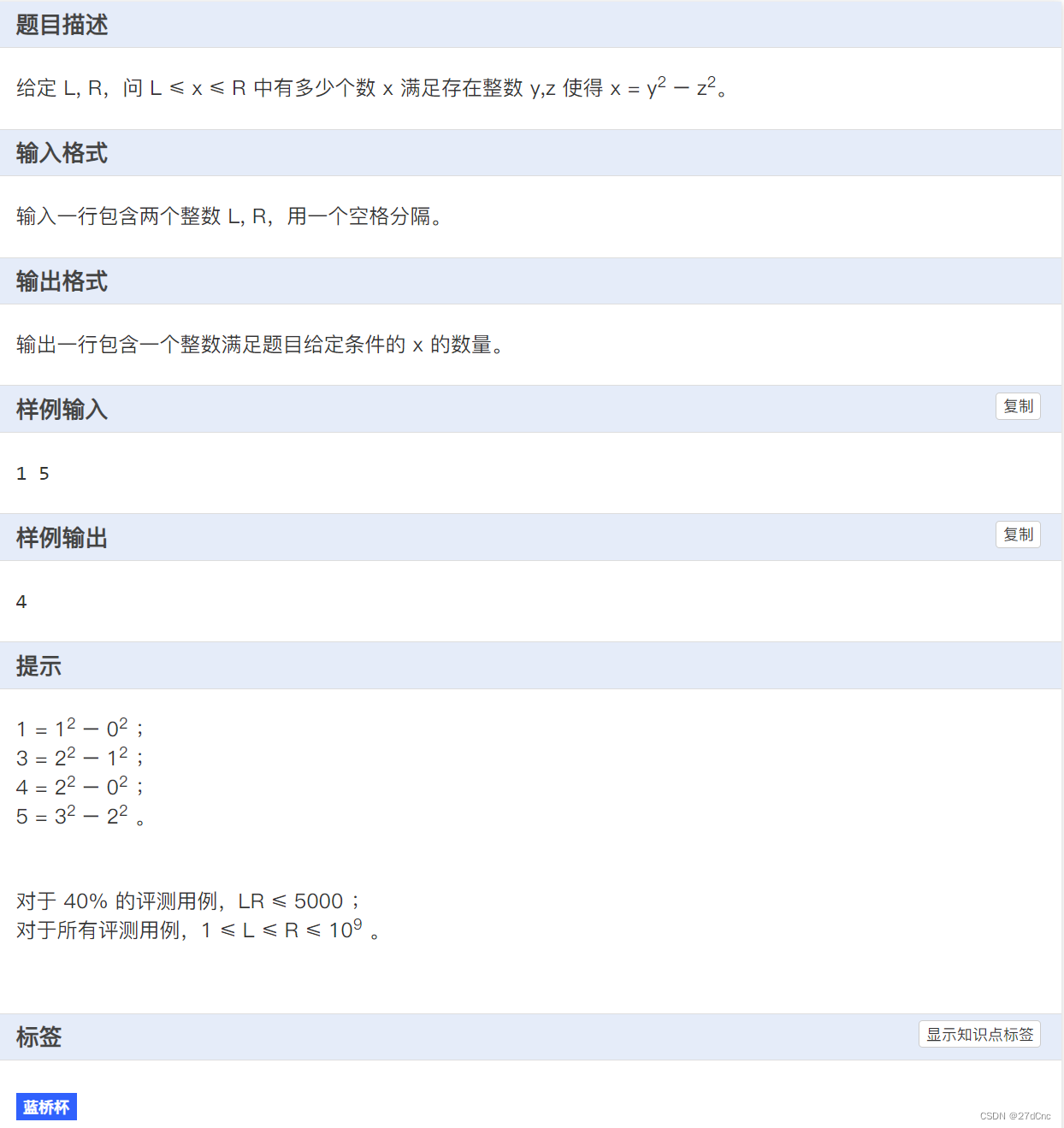
题目描述 给定 L, R，问 L ≤ x ≤ R 中有多少个数 x 满足存在整数 y,z 使得 x = y2 − z2。 思路 首先想到：x²-y²=(x+y)(x-y)，首先如果是奇数2*n+1，肯定可以分成(n+1+n)*(n+1-n)的形式，所以奇数是肯定可行的，然后是偶数2*n，如果凑成(x+y)*(x-y)的形式，则(x+y)或(x-y)中的一个肯定是偶数，并且当一个是偶数时，另一

[蓝桥杯 2023 省 A] 平方差 题目描述 给定 L , R L,R L,R，问 L ≤ x ≤ R L \leq x \leq R L≤x≤R 中有多少个数 x x x 满足存在整数 y , z y,z y,z 使得 x = y 2 − z 2 x=y^2-z^2 x=y2−z2。 输入格式 输入一行包含两个整数 L , R L,R L,R，用一个空格分隔。 输出格式

题目考点: 平方差 ,平方差奇偶关系   代码 #include<bits/stdc++.h>#define Run 0#define endl "\n"#define N 100005using unl = __int128_t;using ll = long long;using namespace std;class Solution {public: vo

分析：x=(y+z)*(y-z); y+z        与        y-z        同奇偶性（x要么为奇数，要么为偶数） 奇数：1        与        其本身   乘积 偶数：2        与        x/2         乘积(为4的倍数) #include<bits/stdc++.h>using namespace std;int

常用数学公式汇总 一、基础代数公式 1. 平方差公式：(a＋b)×(a－b)＝a2－b2 2. 完全平方公式：(a±b)2＝a2±2ab＋b2 完全立方公式：(a±b)3=(a±b)(a2 ab+b2) 3. 同底数幂相乘: am×an＝am＋n(m、n为正整数,a≠0) 同底数幂相除：am÷an＝am－n(m、n为正整数,a≠0) a0＝1(a≠0) a-p＝ (a≠0,p为正整数) 4. 等