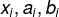基础介绍： 给定给定区间，函数连续且，那么根据介值定理，函数必然在区间内有根。 二分法：将区间不断二分，使端点不断逼近零点。下一次迭代的区间为或，其中。割线法（线性插值）：基本思想是用弦的斜率近似代替目标函数的切线斜率，并用割线与横轴交点的横坐标作为方程式的根的近似。即给定两个点,。其割线方程为，那么令，x的值即为下一次迭代的结果。逆二次插值法：为割线法的进化版本。使用三个点确定一个二次函数，

1. 解方程（Solving Equations） 1.1 二分法（The Bisection Method） 定义1.1 对于方程 ，如果有 ，则说   是  的一个根。 定理1.2 令   是   上的连续函数，满足   , 则   在   和   之间存在一个根。 二分法算法流程： 二分法误差： 在区间  ，