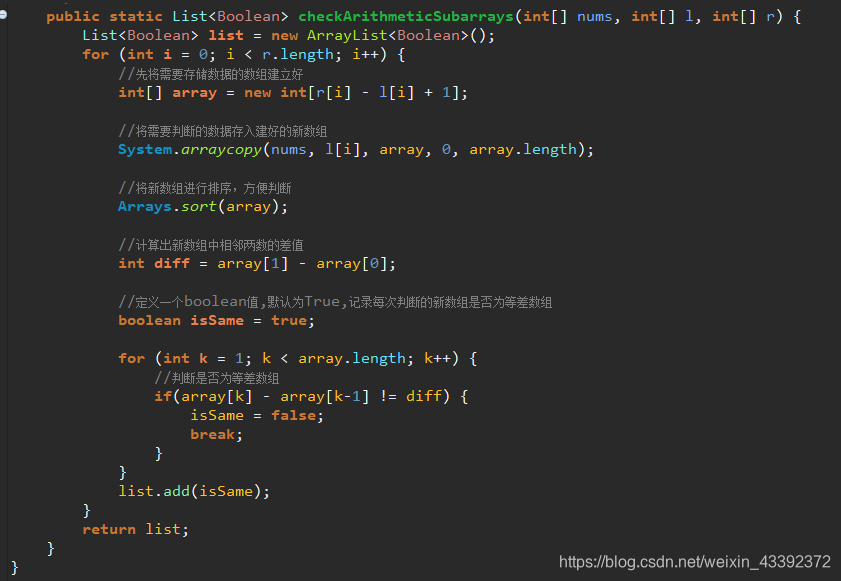
题目描述 给你一个整数数组 arr 和一个整数 difference，请你找出并返回 arr 中最长等差子序列的长度，该子序列中相邻元素之间的差等于 difference 。 子序列 是指在不改变其余元素顺序的情况下，通过删除一些元素或不删除任何元素而从 arr 派生出来的序列。 示例 ： 输入：arr = [1,5,7,8,5,3,4,2,1,0], difference = -2 输

目录 1.最长定差子序列1.题目链接2.算法原理详解3.代码实现 2.最长的斐波那契子序列的长度1.题目链接2.算法原理详解3.代码实现 1.最长定差子序列 1.题目链接 最长定差子序列 2.算法原理详解 思路： 确定状态表示 -> dp[i]的含义 以i位置元素为结尾的所有子序列中，最长的等差子序列的长度 推导状态转移方程 优化： 将元素 + dp[j]

等差子数组 #给你一个由 n 个整数组成的数组 nums，和两个由 m 个整数组成的数组 l 和 r， 后两个数组表示 m 组范围查询，其中第 i 个查询对应范围 [l[i], r[i]] 。所有数组的下标都是 从 0 开始 的。 ！！！切记，一定要理清楚题目的思路哦，像我刚开始就是没有理清题目，导致后续花很多时间.

题目描述： 给定一个整数数组 A，返回 A 中最长等差子序列的长度。 回想一下，A 的子序列是列表 A[i_1], A[i_2], …, A[i_k] 其中 0 <= i_1 < i_2 < … < i_k <= A.length - 1。并且如果 B[i+1] - B[i]( 0 <= i < B.length - 1) 的值都相同，那么序列 B 是等差的。 示例 1： 输入：[3,6,9

Description 给一个1到N的排列{Ai}，询问是否存在1<=p1=3），使得Ap1,Ap2,Ap3,…ApLen是一个等差序列。 Input 输入的第一行包含一个整数T，表示组数。下接T组数据，每组第一行一个整数N，每组第二行为一个1到N的排列，数字两两之间用空格隔开。 Output 对于每组数据，如果存在一个等差子序列，则输出一行“Y”，否则输出一行“N”。 Sample