审敛专题
两种正项级数比较审敛法极限形式的不同表述
正项级数的比较审敛法是较好用的方法。尤其是它的极限形式更为常用。 在一般高数书本上,表述如下: 设 limn→+∞unvn=l,l∈[0,+∞] \lim_{n\rightarrow +\infty}{u_n\over v_n} = l, l\in [0,+\infty] 则: 若 0<l<+∞ 0 < l < +\infty, ∑∞n=1un
级数@常数项级数@正项级数审敛法总结
文章目录 级数定义敛散性余部 级数的性质基于定义的重要的基础级数模型p级数几何级数 正项级数收敛定理审敛法正项级数两大类审敛法的比较 级数定义 设有数列 { u n } = u 1 , u 2 , ⋯ \set{u_n}=u_1,u_2,\cdots {un}=u1,u2,⋯ 前 n n n项和为 S n = ∑ i = 1 n u i S_n=\sum\limits_
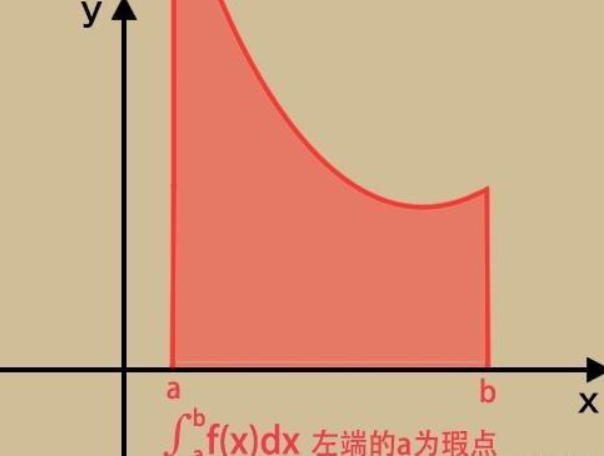
高数 | 定理及性质证明 | 反常积分审敛法为什么只需要看瑕点
总结 注:这里的两个应该为同阶无穷大 注:这里的两个为同阶无穷小!总结为:同阶同敛散 拓展:瑕点 反常积分中的瑕点的含义:如果函数f(x)在点a的一个邻域内无界,那么点a称为函数f(x)的瑕点(也称无界间断点)。无界函数的反常积分又称为瑕积分。如果函数在点a的任一临域内都无界的意思是被积函数的第二类间断点
高数 | 【无穷级数】等价无穷小(Talor展开)判敛法 交错级数不能用通项等价关系审敛
一、引例 我们知道,对于正项级数可以利用所谓的通项等价关系进行审敛,即 废话不多说,看例题 : 二、经错标零 例题你觉得简单?下面这坑你必踩~ 经典的错误,标准的零分~ 关注A选项~ 你的做法: 应用性质:在级数中加上或减去有限项后级数的敛散性不变 设从某一项 N 之后, 运用等价无穷小 如果按照交错级数审敛法(莱布