叉积专题
利用向量积(叉积)计算三角形的面积和多边形的面积(hdu2036)
开始撸计算几何题目了。。。。。。。 预备知识:叉乘求多边形面积 参考证明资料: 公式证明: http://www.cnblogs.com/xiexinxinlove/p/3708147.html 高中知识: http://wenku.baidu.com/view/867e6edfad51f01dc281f11a.html #include<stdio.h>#inclu
poj 3304 Segments(计算几何:叉积)
题目给出多条线段,问是否存在一条直线 使得所有投射到这条直线的线段至少有一个交点 也即判断是否存在一条直线与所有线段都相交 假设存在一条直线与所有线段都相交,那么我们一定可以通过平移、旋转等处理 使这条直线与两条或多条线段交于线段的端点处 我们就可以通过枚举所有端点再判断这样的直线是否满足条件即可 代码如下: /* ********************************
poj 2398 Toy Storage(计算几何:叉积)
基本上和poj 2318一模一样。。。 改下输出就可以了 代码如下: /* ***********************************************Author :yinhuaCreated Time :2014年12月01日 星期一 19时25分15秒File Name :poj2398.cpp*******************
FZU 2148(计算几何)叉积模板
题目链接:点击打开链接 题目分析:凸四边形个数判断,枚举法。 Sacb+Sabd+Sacd=Sbcd; 则为凹多边形。 题目总结:i,j,k,l一多,j++写成i++ wa了好几炮 此题可为为模板了 #include <cmath>#include <cstdio
poj2318(叉积计算点与直线的关系)
题目链接:http://poj.org/problem?id=2318 水水的一道题哇!(来熟悉模板, 哈哈) 判断toys的位置。 思路很简单,叉乘就可以知道点与直线的关系;比如xmult(point p1, point p2, point p0)>0 p1在直线的左侧(p2,p0是直线的端点,左右理解为眼睛顺着直线的方向的左右)。 #include
poj 3348 Cows (叉积计算凸包面积)
题意挺简单的,求凸包的面积然后除于50即可。 面积:固定某一点,找枚举凸包中的点,用叉积求即可: #include <iostream>#include <cstdio>#include <cmath>#include <stack>#include <algorithm>#define PI acos(-1)#define MAXN 1000+10using namespa
叉积判断点在多边形内外 poj2318
计算几何中长遇到的问题:判断特定点是否在平面多边形内部。向量叉积是一种方法,用于凸多边形。【优角:角度值大于180度小于360度。凸多边形:沿着多边形的一边做一条直线,如果剩下所有的部分都在直线的同侧,那么称这是一个凸多边形,凸多边形是没有优角的】 判断:连接第i条边的第一个端点和测试点成向量u,再连接第一个端点与第二个端点成向量v,记录叉积结果,除第一条边外,叉积结果和上一条边对应的叉积的乘积
#叉积#ssl 1715 计算面积
题目 输入三个点的坐标,输出由该三个点组成的平行四边形的面积 分析 按照叉积的定义,其实这道题就是求叉积的绝对值,在此直接放出代码,不过叉积为0时输出Error 代码 #include <cstdio>#include <cctype>#define rr registerusing namespace std;inline signed iut(){rr int ans
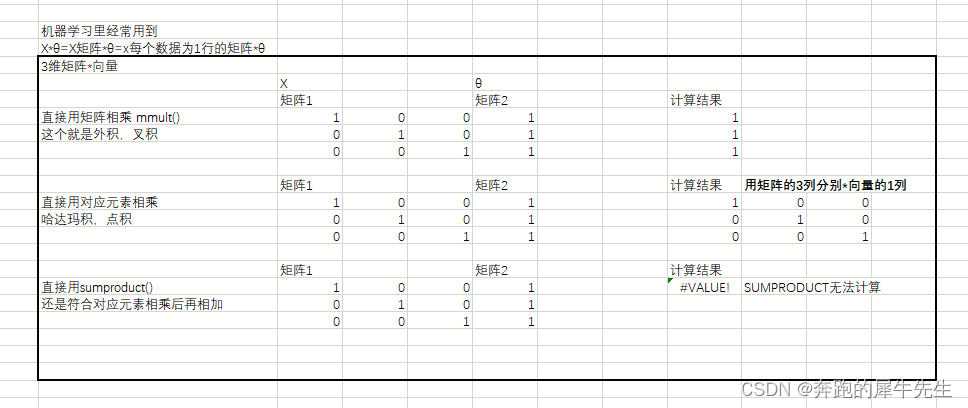
线性代数的学习和整理23:用EXCEL和python 计算向量/矩阵的:内积/点积,外积/叉积
目录 1 乘法 1.1 标量乘法(中小学乘法) 1.1.1 乘法的定义 1.1.2 乘法符合的规律 1.2 向量乘法 1.2.1 向量:有方向和大小的对象 1.2.2 向量的标量乘法 1.2.3 常见的向量乘法及结果 1.2.4 向量的其他乘法及结果 1.2.5 向量的模长(长度) 模长的计算公式 1.2.6 距离 2 向量的各种乘法 2.1 向量的标量乘法(
POJ—2318 TOYS(叉积判断点和直线关系)
题目: Calculate the number of toys that land in each bin of a partitioned toy box. Mom and dad have a problem - their child John never puts his toys away when he is finished playing with them. They ga
sincerit 内心里的一把火(叉积公式求面积)
链接:https://ac.nowcoder.com/acm/contest/289/D 来源:牛客网 题目描述 小明在上学的路上,看到了小花,小花也看见了他,两个人深情的对视了一下,然后小花就对小明说:你爱过我吗?小明说:爱过。小花就对小明说,那你能帮我做一个题目吗?如果你能做对的话,就证明你爱过我。小明自信的回答好啊。小花说,给你三个人的坐标,以及小花的坐标,她想知道她是不是处在他们三个人
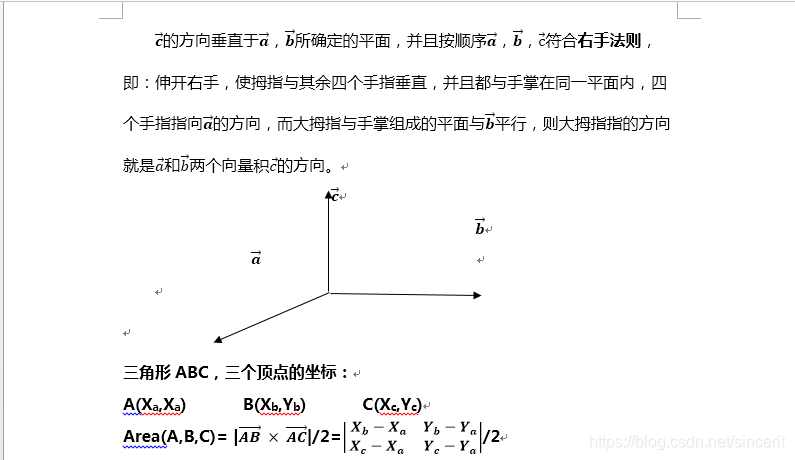
如何证明向量的叉积公式?
叉积是向量的两种主要运算之一。我们设两个空间三维向量分别为 a = ( a x , a y , a z ) , b = ( b x , b y , b z ) \bm{a}=(a_x,a_y,a_z),b=(b_x,b_y,b_z) a=(ax,ay,az),b=(bx,by,bz)三维向量的叉积的两种定义分别为 c = a × b = ( a y b z − a z b y ,
极角排序:POJ 1696(叉积+深搜)
POJ1696题意: 一只很特殊的蚂蚁,只能向坐转,并且不能经过已经走过的路。一张地图上有n个食物让蚂蚁去采集,求蚂蚁经过所有食物的顺序(找出一条最长的非右拐的路径)。 样例: Sample Input 2 (二次测试) 10 (十个食物点) 1 4 5 (点的编号,x坐标,y坐标) 2 9 8 3 5 9 4 1 7 5 3 2
利用叉积计算向量的旋向及折线段的拐向
一、向量叉积 两个向量 u u u、 v v v的叉积写作 u × v = n ∥ u ∥ ∥ v ∥ s i n θ \mathbf{u \times v = n \left \| u \right \| \left \| v \right \| sin\theta } u×v=n∥u∥∥v∥sinθ 式中, n n n: 与 u u u、 v v v均垂直的单位向量,theta是两向量的夹角
POJ 2318 TOYS 二分+叉积
入门计算几何 判断在哪个区域内只需看跟某条线的叉积即可 可以保证单调性,所以可以进行二分 #include <iostream>#include <cstdio>#include <cstring>#include <string>#include <algorithm>#include <cstdlib>#include <cmath>#include <ma
闲聊叉积在计算几何中一些作用
定义 两个向量的叉积写作a×b,可以定义为 a×b=absinθn 其中θ表示a和b之间的角度(0°≤θ≤180°)。它位于这两个矢量所定义的平面上。而n是一个与a、b所在平面均垂直的单位矢量。矢量叉积是计算几何算法的核心部分,具有重要的几何意义。 一、计算多边形面积 设多边形有n个顶点V0(X0, Y0), V1(X1, Y1)... Vn-1(Xn-1, Yn-1),从原点O(0,0)与每条