卡诺图专题
卡诺图:逻辑相邻与几何相邻的统一
文章目录 1.一句话记住卡诺图2.卡诺图的由来、定义和特点3.填写卡诺图(用卡诺图表示逻辑函数)⑴根据真值表填写卡诺图⑵根据最小项(或最大项)填写卡诺图⑶根据函数的与或表达式填写卡诺图 4.用卡诺图化简逻辑函数⑴化简步骤⑵画圈原则 综合题★★★后记:关于列表法(Q-M法) 今天是南方小年,春节渐近,提前祝大家新春快乐! 这节内容斟酌再三,今天终于成稿,主要是希望内容既全面又易
【数电复习】逻辑函数的表示方法及互相转换(表达式、真值表、逻辑图、波形图、卡诺图)(手把手教版(雾
目录 #前言 一、逻辑函数表示方法的基本了解 1、逻辑函数表达式 2、真值表 3、逻辑图 逻辑运算 4、波形图 5、卡诺图(用来化简表达式,非常
Karnaugh map (卡诺图)
【Leetcode】 289. Game of Life According to Wikipedia’s article: “The Game of Life, also known simply as Life, is a cellular automaton devised by the British mathematician John Horton Conway in 1970.”
卡诺图:逻辑相邻与几何相邻的统一
文章目录 1.一句话记住卡诺图2.卡诺图的由来、定义和特点3.填写卡诺图(用卡诺图表示逻辑函数)⑴根据真值表填写卡诺图⑵根据最小项(或最大项)填写卡诺图⑶根据函数的与或表达式填写卡诺图 4.用卡诺图化简逻辑函数⑴化简步骤⑵画圈原则 综合题★★★后记:关于列表法(Q-M法) 今天是南方小年,春节渐近,提前祝大家新春快乐! 这节内容斟酌再三,今天终于成稿,主要是希望内容既全面又易
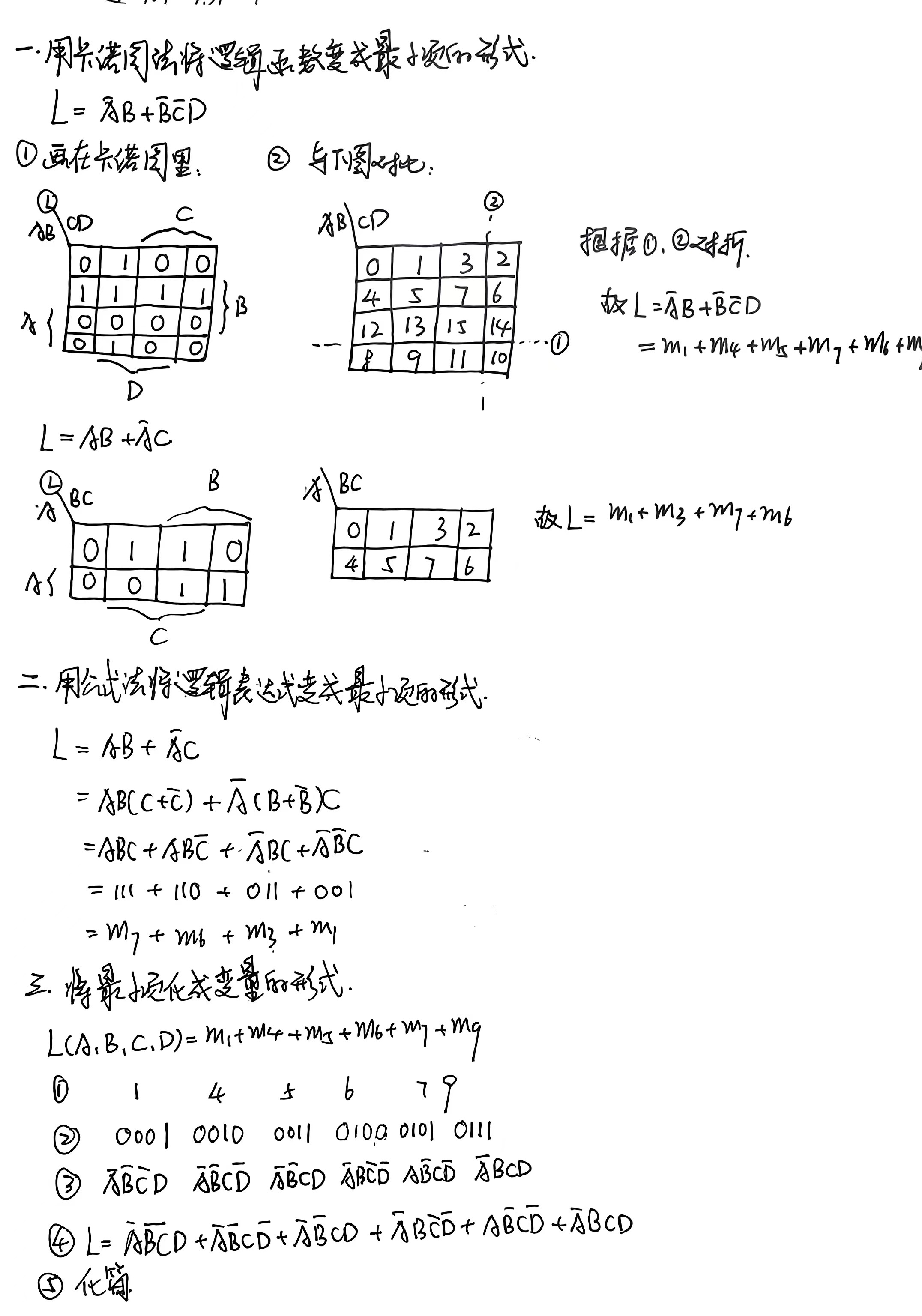
利用卡诺图对逻辑表达式进行化简
一、循环码 1. 循环码的定义 又称做格雷码。格雷码属于可靠性编码,是一种错误最小化的编码方式,因为,自然二进制码可以直接由数/模转换器转换成模拟信号,但某些情况,例如从十进制的3转换成4时二进制码的每一位都要变,使数字电路产生很大的尖峰电流脉冲。而格雷码则没有这一缺点,它是一种数字排序系统,其中的所有相邻整数在它们的数字表示中只有一个数字不同。它在任意两个相邻的数之间转换时,
12.12进制(原反补码,运算,进制转换),卡诺图化简,组合逻辑电路(竞争冒险,分析、设计方法),杂项
逻辑代数的基本定理和规则是用来处理逻辑函数的,其中包括以下几个重要的定理和规则: 1. 与门的性质: - 同一律:A∧A=A - 零律:A∧0=0 - 一律:A∧1=A 2. 或门的性质: - 同一律:A∨A=A - 零律:A∨0=A - 一律:A∨1=1 3. 非门的性质: - 否定律:¬(¬A)=A 4. 交换律: - 与门交换律:A∧B=B∧A - 或门交换律:A∨B=B∨A