公约数专题
有关于递归函数的一些学习记录(Recursion)走楼梯,递归找出最两个数的大公约数,汉诺塔问题
递归函数的定义是指在函数执行的过程中,在函数体中直接或间接的调用了自己,这样的函数就是递归函数。递归函数的使用使得分而制之(Divide and Conquer)的思想得意实现,并在解决循环和一些复杂的求解问题中显示了很好的作用。 问题一:说,一个人在爬一个楼梯时,一次可以走一个台阶也可以走两个台阶,问这个人走到第九个台阶有多少种走法? 这是我在2013年春参加南京大学计
一个求公约数和公倍数的有趣求法
代码: #include<stdio.h> #include<algorithm> using namespace std; int gcd(int x, int y) { while(x^=y^=x^=y%=x); return y; } int f(int x, int y) { return x * y / gcd(x, y); } int main() { int
【AcWing】蓝桥杯集训每日一题Day25|最大公约数|算数基本定理|4199.公约数(C++)
4199.公约数 4199. 公约数 - AcWing题库难度:中等时/空限制:1s / 256MB总通过数:2801总尝试数:7059来源:AcWing第30场周赛算法标签最大公约数试除法二分 题目内容 给定两个正整数 a 和 b。 你需要回答 q 个询问。 每个询问给定两个整数 l,r,你需要找到最大的整数 x,满足: x 是 a 和 b 的公约数。l≤x≤r。 输入格式 第一
【蓝桥杯每日一题】4.8 公约数
题目来源: 4199. 公约数 - AcWing题库 问题描述: 找到最大整数x,需满足下面两个条件 x x x是 a a a, b b b的公约数 l < = x < = r l<=x<=r l<=x<=r 思路: 找到 a a a, b b b两个数的最大公约数 g c = g c d ( a , b ) gc=gcd(a,b) gc=gcd(a,b)将此最大公约数的所有约数
蓝桥杯每日一题:公约数(gcd)
题目描述: 给定两个正整数 a 和 b。 你需要回答 q 个询问。 每个询问给定两个整数 l,r,你需要找到最大的整数 x,满足: x 是 a和 b 的公约数。l≤x≤r。 输入格式 第一行包含两个整数 a,b。 第二行包含一个整数 q。 接下来 q 行,每行包含两个整数 l,r。 输出格式 每个询问输出一行答案,即满足条件的最大的 x�,如果询问无解,则输出 −1−1。 数
【二进制求公约数】【数学】【数论】2543. 判断一个点是否可以到达
本文涉及知识点 二进制求公约数 LeetCode2543. 判断一个点是否可以到达 给你一个无穷大的网格图。一开始你在 (1, 1) ,你需要通过有限步移动到达点 (targetX, targetY) 。 每一步 ,你可以从点 (x, y) 移动到以下点之一: (x, y - x) (x - y, y) (2 * x, y) (x, 2 * y) 给你两个整数 targetX 和 targe
最小公约数,python怎么写,C++(2011/boost)就也怎么写
http://lionelliu.com/?p=1729 def gcd(a, b): while b: a, b = b, a % b return a int gcd(int a, int b) { while (b) { tie(a, b) = make_pair(b, a % b
我与代码的日常:交换变量值,求最大值,求公约数和公倍数
学习不易,需要坚持 1.交换两个变量值 2.求10个整数的最大值 3.将三个数从大到小输出 4.求两个数的最大公约数最小公倍数 //交换两个数字的值(常规方法,借助中间变量来交换)#include <stdio.h>void Swap(double* p1, double* p2){double temp = *p1 ;*p1 = *p2 ;*p2 = temp ;}int mai
求两个数所有的公约数
题目描述: 给定两个正整数a,b(1<=a,b<=100000000),计算他们公约数的个数。 如给定正整数8和16,他们的公约数有:1、2、4、8,所以输出为4。 输入: 输入包含多组测试数据,每组测试数据一行,包含两个整数a,b。 输出: 对于每组测试数据,输出为一个整数,表示a和b的公约数个数。 样例输入: 8 1622 16 样
20240112公约数与公倍数
代码 def gcd(x, y):while y:x, y = y, x % yreturn xdef lcm(x, y):return x * y // gcd(x, y)num1 =12 num2=18print(gcd(num1,num2)) # 6print(lcm(num1,num2)) #36 概念 公约数 在数学中,两个或多个整数的公约数是能够整除它们的正整数
3的幂[递归/循环 || 公约数]
3的幂 前言一、3的幂二、直接法 & 数学法1、递归与循环2、3的最大幂与约数 总结参考文献 前言 3的幂,可不断除3来判定一个数是否为3的幂,有两种方式,一种递归判定,没有循环结构,代码简单&速度稍快,就是需要函数栈的内存开销;而递归的方式稍慢,但是代码容易理解 & 没有函数栈的内存开销。除此之外,能数学化,是解题的最高境界(当可以数学化时),而通过拿到3的最大幂来对n进行取余
南阳oj 题目40 公约数和公倍数
公约数和公倍数 时间限制: 1000 ms | 内存限制: 65535 KB 难度: 1 描述 小明被一个问题给难住了,现在需要你帮帮忙。问题是:给出两个正整数,求出它们的最大公约数和最小公倍数。 输入 第一行输入一个整数n(0<n<=10000),表示有n组测试数据; 随后的n行输入两个整数i,j(0<i,j<=32767)。 输出 输出每组测试数据的最大
求分数与分数,分数与整数,整数与整数最小公倍数及最小公约数
一、分数与分数,分数与整数最小公倍数求法 1.先把分母化为相同,在求分子的最小公倍数2,把整数化为与分数同分母的分数,在求分子的最小公倍数最后,把分数化为最简的形式。 二、整数与整数最小公倍数 最小公倍数=两整数的乘积÷最大公约数 求最大公约数算法: (1)辗转相除法 有两整数a和b: ① a%b得余数c ② 若c=0,则b即为两数的最大公约数 ③ 若c≠0
Python输出1-100之间的奇数,求最小公约数的两个代码程序段
目录 前言 一、输出1-100之间的奇数 1.实现的功能 2.代码程序 3.运行截图 二、求最小公约数 1.实现的功能 2.代码程序 3.运行截图 前言 1.因多重原因,本博文由两个程序代码部分组成,如果想使用快速查找,建议浏览目录检索; 2.本代码为Python语言,我使用的是Spyder(python 3.8)软件,所有关于Python的博文,只发布Python的执



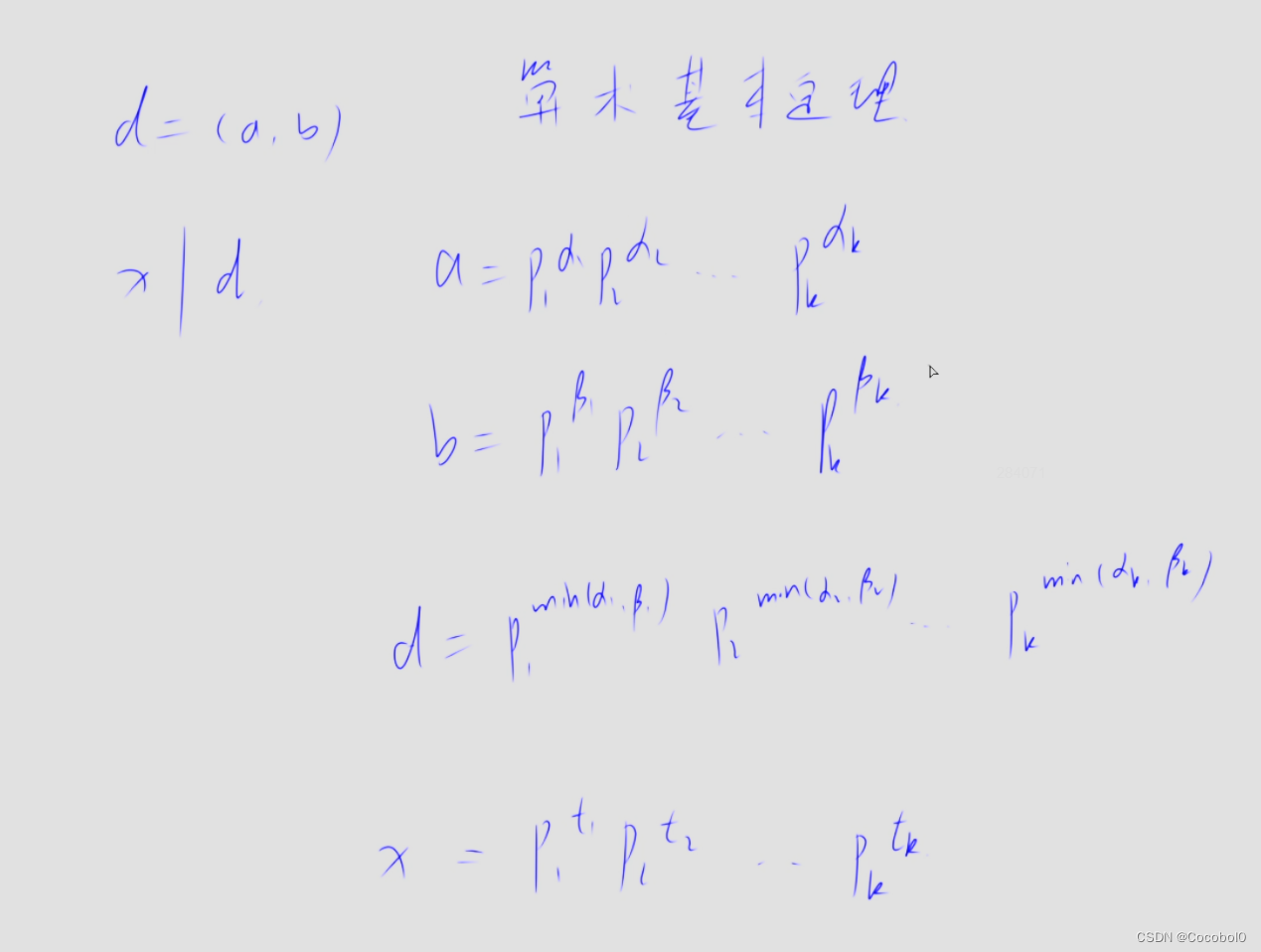


![3的幂[递归/循环 || 公约数]](https://img-blog.csdnimg.cn/98aedbbcaad94b709a3d69962b74482a.png)
