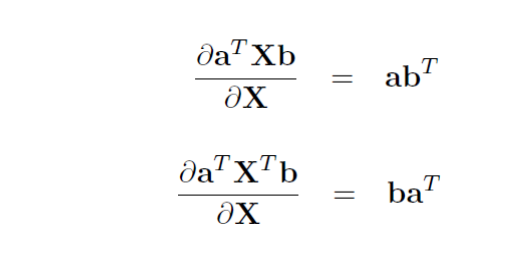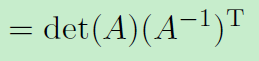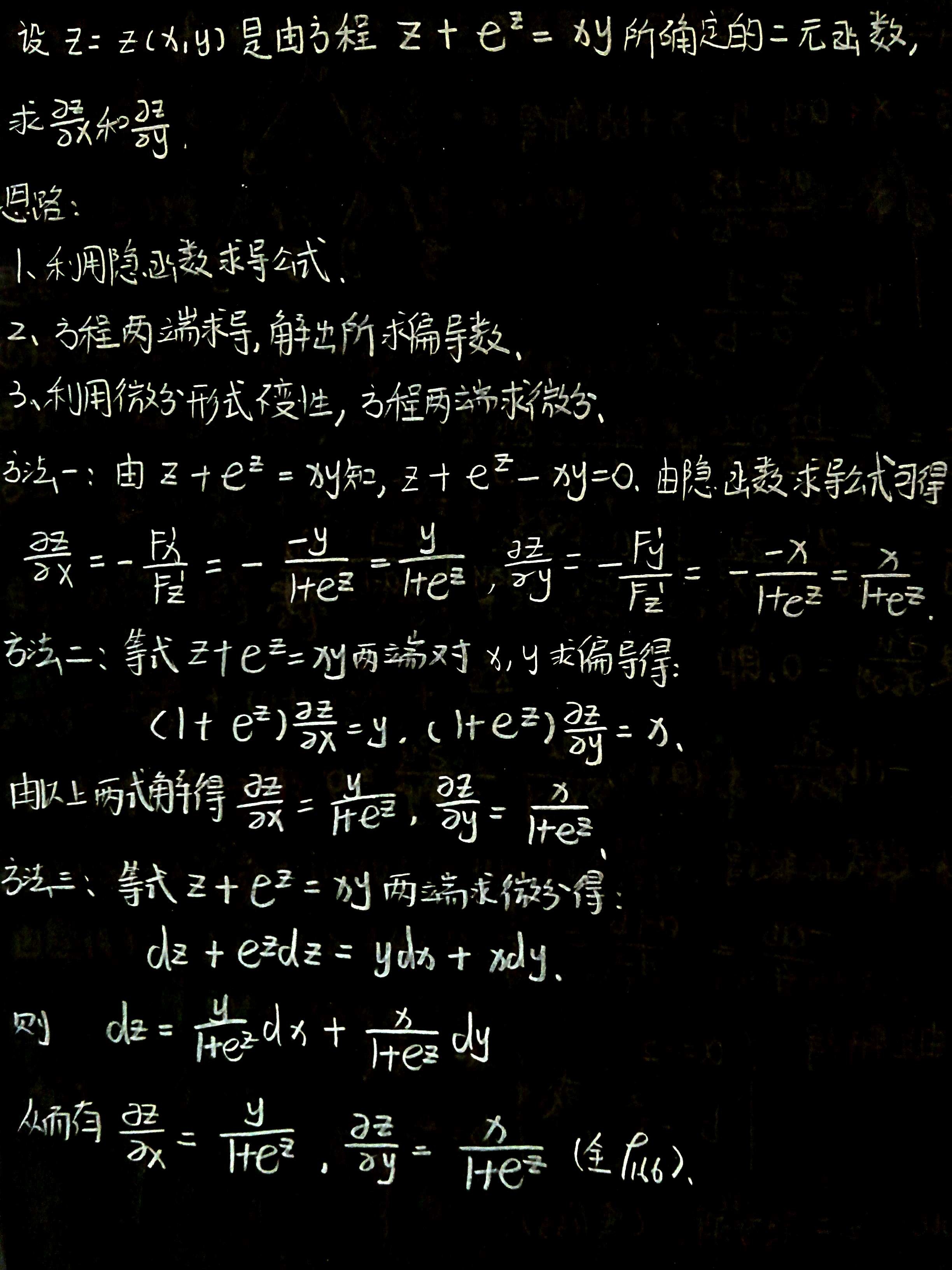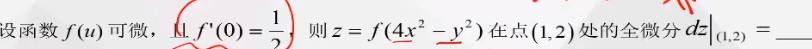矩阵的迹求导法则 1. 复杂矩阵问题求导方法：可以从小到大，从scalar到vector再到matrix 2. x is a column vector, A is a matrix d(A∗x)/dx=A d(A*x)/dx=A d(xT∗A)/dxT=A d(x^T*A)/dx^T=A d(xT∗A)/dx=AT d(x^T*A)/dx=A^T d(xT

线性代数之行列式偏导 矩阵偏导 针对y或者f(x)是元素，x是矩阵的情况，则元素对矩阵的求导形式如下： 注:这里的 ​ 和矩阵x是同型（行数列数相同）的。 行列式性质 这里假定A是方阵，则有如下性质： 1 余子式是将行列式的第i行、第j列删除后组成的新行列式，一般用如下符号表示： 比较一般的例子(M11)见： 2

多元隐函数三种求偏导方法

转载出处：https://www.zhihu.com/question/40181086?sort=created 教科书上有严格的证明，这个答案试图通过类比来提供一些直观上的理解。大概的结论是，多元函数的Hessian矩阵就类似一元函数的二阶导。多元函数Hessian矩阵半正定就相当于一元函数二阶导非负，半负定就相当于一元函数二阶导非正。如果这个类比成立的话，凸函数的Hessian

显函数求偏导 方法一、将y看作常数，转变成x的一元函数，转化成一元函数求偏导的过程 方法二、对x求偏导，令y直接等于0，然后求导 复合函数求偏导 1、将f看作u的一元函数，u看作xy的二元函数 2、df/dx=df/dududx 3、可以直接带入y=2，求x的偏导 4、可以直接带入x=1，求y的偏导

无论单变量对向量，向量对向量，矩阵对向量，矩阵对单变量，矩阵对矩阵等等各种排列组合的结果的求导组合 即A中每个元素对B中每个元素的偏导数 转载至知乎