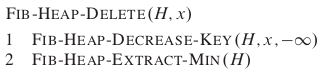问题一：写一个函数，输入n，求斐波那契数列的第n项？      实用的解法：从下往上计算，首先根据f(0)和f(1)算出f(2)，在根据f(1)和f(2)计算出f(3)...依次类推算出第n项。这种思路的时间复杂度为o(n)。   代码：        问题二：一只青蛙一次可以跳上1级台阶，也可以跳上2级台阶，求该青蛙跳上一个n级的台阶总共有多少种跳法？      如果只有1级台

目录 前言一、查找算法预备知识二、斐波那契查找三、总结3.1 查找性能3.2 适用场景 前言 查找算法是一种用于在数据集合中查找特定元素的算法。在计算机科学中，查找算法通常被用于在数组、链表、树等数据结构中查找目标元素的位置或者判断目标元素是否存在。 查找算法的目标是在尽可能短的时间内找到目标元素，以提高程序的效率和性能。常见的查找算法包括但不限于二分查找、哈希表查找、线性

蓝桥集训之斐波那契前n项和 核心思想：矩阵乘法 左边求和 右边求和 得到Sn = fn+2 – 1 因此只要求出fn+2 即可 #include <iostream>#include <cstring>#include <algorithm>using namespace std;typedef long long LL;int n,m;int A[2][2] = { //构

一、动态规划的算法原理         这是本人动态规划的第一篇文章，所以先阐述一下动态规划的算法原理以及做题步骤。动态规划本人的理解就是通过题目所给的条件正确地填满dp表（一段数组）。首先要先确定好dp表每个位置的值所代表的含义是什么，然后通过题目条件以及经验推出状态转移方程，第三个就是初始化，确定填表顺序以及保证填表不越界，最后输出题目所需的结果，大致就是这个思路。 二、斐波那契数列模型例

算法沉淀——动态规划之斐波那契数列模型 01.第 N 个泰波那契数02.三步问题03.使用最小花费爬楼梯04.解码方法 动态规划（Dynamic Programming，简称DP）是一种通过将原问题分解为相互重叠的子问题并仅仅解决每个子问题一次，将其解存储起来，避免重复计算，从而提高效率的算法优化技术。它通常用于求解最优化问题。 动态规划的基本思想是利用之前已经计算过的结果

堆的变体： 二叉堆 二项堆 斐波那契堆 前面的博客中我们讲到的堆的两种变体，二叉堆和二项堆，今天我们要讲的就是著名的斐波那契堆。 依然首先列出了三种堆的时间复杂的比较。 从上面能发现斐波那契堆的时间复杂度在很多操作上有优化，如insert, minimum, union , decrease-key，而extreact-min，delete没有变化。 可能看到

Java数据结构与算法：动态规划之斐波那契数列 大家好，我是免费搭建查券返利机器人赚佣金就用微赚淘客系统3.0的小编。在这寒冷的季节里，让我们一同探讨Java中的动态规划，重点关注解决问题的经典代表之一——斐波那契数列。 动态规划简介 动态规划是一种解决问题的数学方法，通常用于优化递归算法。它通过将问题分解为子问题并保存它们的解，避免重复计算，从而提高算法效率。在动态规划的应用中，最常见的问

动态规划1.0 动态规划 - - - 斐波那契数列模型1. 第 N 个泰波那契数2. 三步问题3. 使用最小花费爬楼梯4. 解码方法 动态规划 - - - 斐波那契数列模型 1. 第 N 个泰波那契数 题目链接 -> Leetcode -1137. 第 N 个泰波那契数 Leetcode -1137. 第 N 个泰波那契数 题目：泰波那契序列 Tn 定义如下： T0 =

斐波那契数列（Fibonacci sequence），又称黄金分割数列，因意大利数学家莱昂纳多·斐波那契（Leonardo Fibonacci）以兔子繁殖为例而引入，故又称为“兔子数列”。         其是指这样一个数列：1、1、2、3、5、8、13、21、34、……第三个数是前两个整数之和。在数学上，其被以递归的方法定义：F(0)=0，F(1)=1, F(n)=F(n -