lorenz transformation 洛伦兹变换算法介绍 洛伦兹变换（Lorentz transformation）是狭义相对论中关于不同惯性系之间物理事件时空坐标变换的基本关系式。这种变换可以用一组数学方程来表示，这组方程描述了如何在两个惯性参考系之间转换坐标和时间。 用于描述两个以恒定速度相对运动的惯性参考系之间的坐标变换。这些变换对于理解时空的相对性至关重要，并且在物理学中有着广泛的

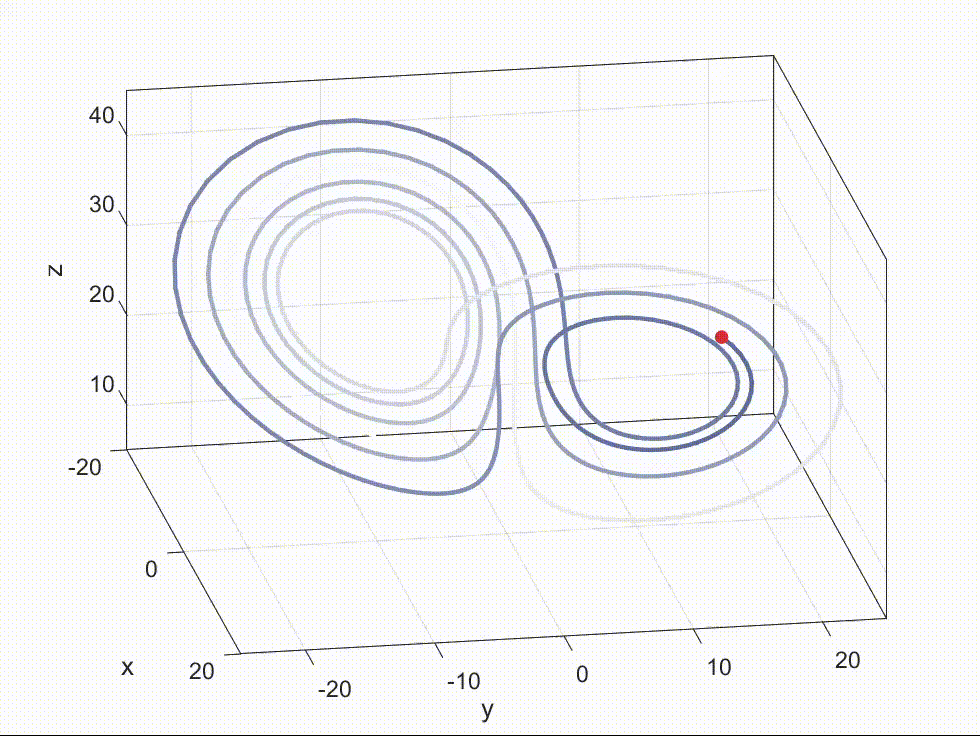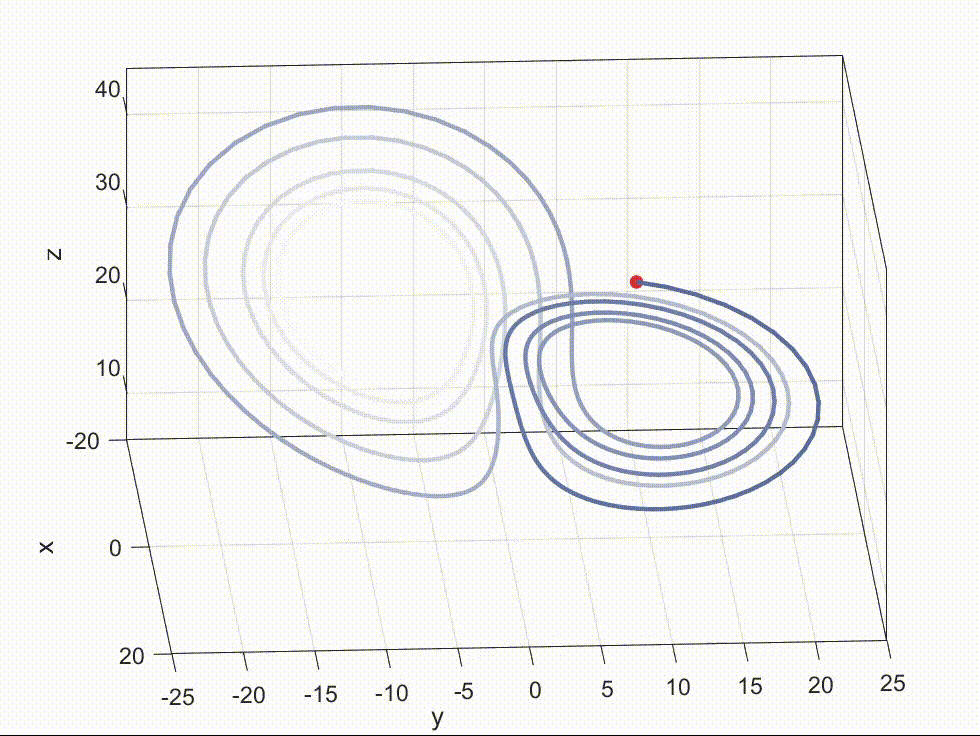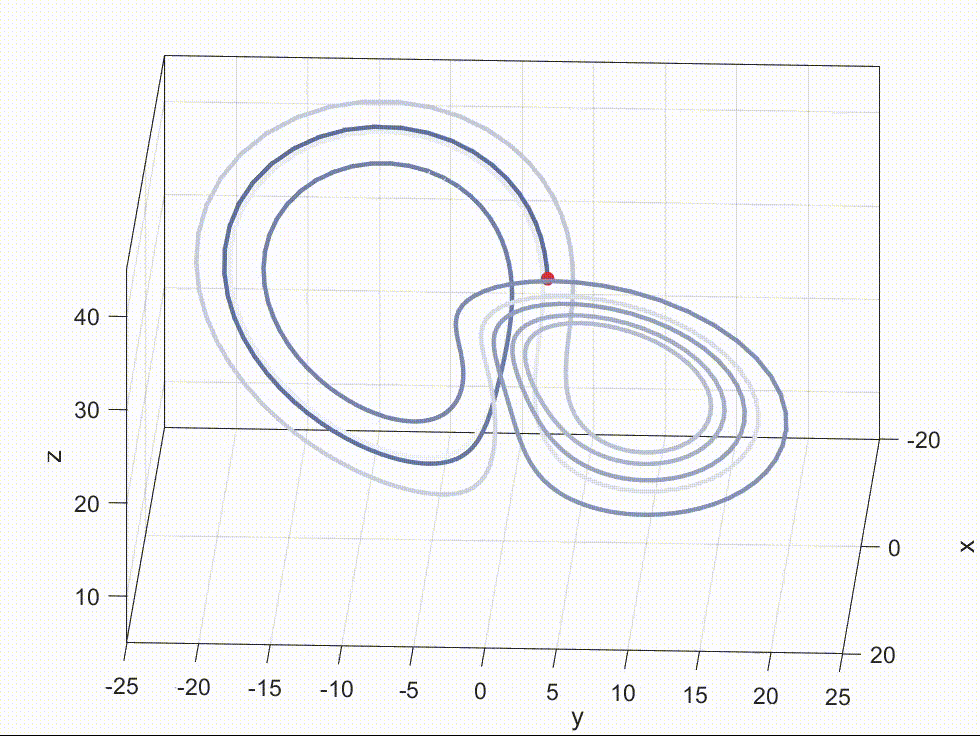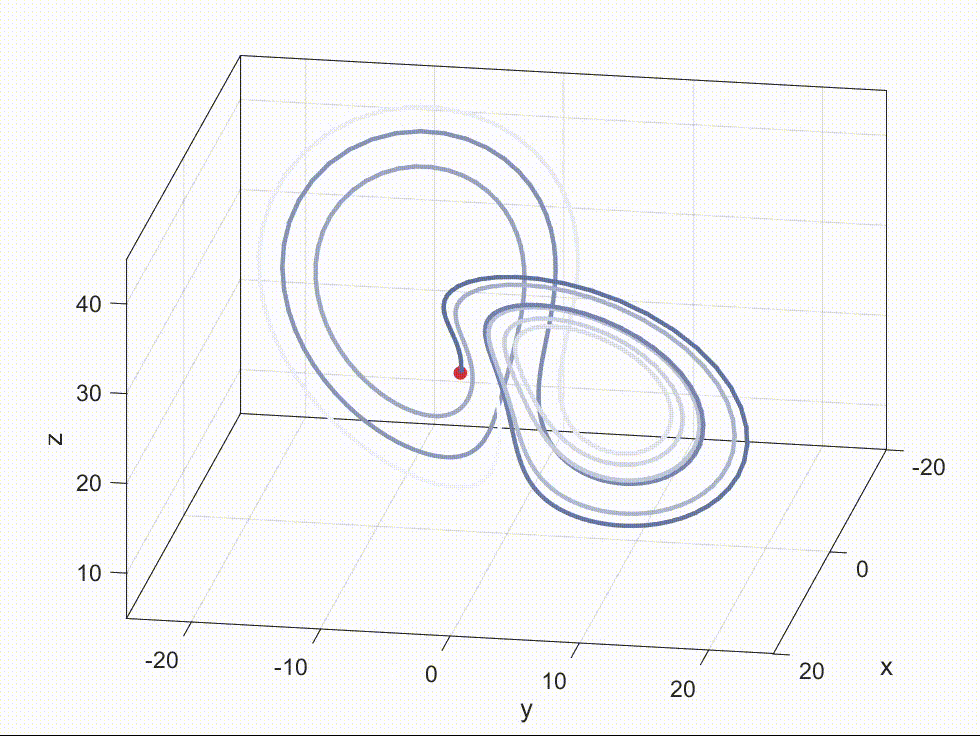
lorenz-x-y-z Lorenz三个维度数据 在科研工作中，经常需要将数据可视化以便更好地理解和传达研究成果。 但大家主要放静态图片，而视频或动画通常比静态图片更具吸引力和表现力。AE, Manim太难学，Matlab就可以用来制作动画。 在这篇博客中，我们将介绍如何使用 MATLAB 制作动画，并以 Lorenz 系统为例进行演示。完整源代码动态Lo

采用庞加莱截面的方式获取lorenz在x=y上的截面值。 一点基础知识： 空间中，计算点面距离。该距离可能为正，也可能为负。 function D = dis(xk, plane)% xk 是一个四维点的坐标，表示为一个 1x4 的向量 [xk1 xk2 xk3 xk4]% plane 是一个包含平面参数的向量，表示为 [a b c d e]% 提取点的坐标和平面的参数xk1 = xk(1)

本小节求解Lorenz微分方程： 在“数学之美”那一章里，为方便读者理解，Lorenz吸引子轨迹的计算采用了比较“原始”的方法。采用integrate模块中的odeint()函数可以更加方便地完成计算。Lorenz吸引子由下述三个微分方程定义： d x d t = σ ( y − x ) , d y d t = x ( ρ − z ) − y , d z d t = x y − β z \fra

#C0403 沧海茫茫千钟粟，且拾吾昧一微尘 ——《沧海拾昧集》@CuPhoenix 【阅前敬告】 沧海拾昧集仅做个人学习笔记之用，所述内容不专业不严谨不成体系 【如有问题必是本集记录有谬，切勿深究】 目录 前言一、S-函数二、实例：Lorenz 混沌系统仿真1、自定义 S-函数2、在 Simulink 中搭建仿真3、仿真结果 三、其他资料