determinant专题
2020ICPC·小米 网络选拔赛第二场 Determinant(行列式)
题意: 按照题目规则组成的矩阵,求行列式值。 思路: 流下了不会线代的泪水,虽然最后推出来了,但是签到题那么久不应该。 按照行列式的性质可以有如下变化 1 2 3 4 5 + x 6 7 8 9 \begin{matrix} 1 & 2 & 3 \\ 4 & 5+x & 6 \\ 7 & 8 & 9 \end{matrix} 14725+x8369 => 1 2 3 4 5
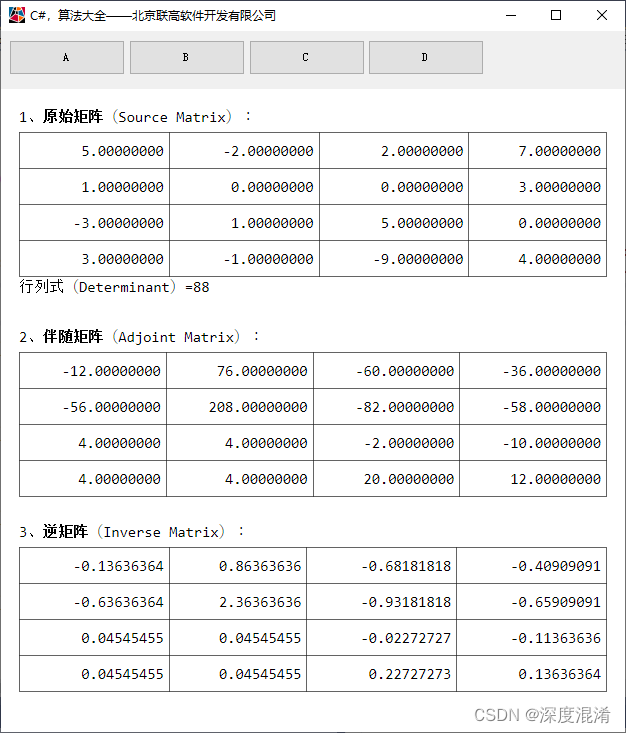
C#,数值计算,矩阵的行列式(Determinant)、伴随矩阵(Adjoint)与逆矩阵(Inverse)的算法与源代码
本文发布矩阵(Matrix)的一些初级算法。 一、矩阵的行列式(Determinant) 矩阵行列式是指矩阵的全部元素构成的行列式,设A=(a)是数域P上的一个n阶矩阵,则所有A=(a)中的元素组成的行列式称为矩阵A的行列式,记为|A|或det(A)。若A,B是数域P上的两个n阶矩阵,k是P中的任一个数,则|AB|=|A||B|,|kA|=kⁿ|A|,|A*|=|A|,其中A*是A
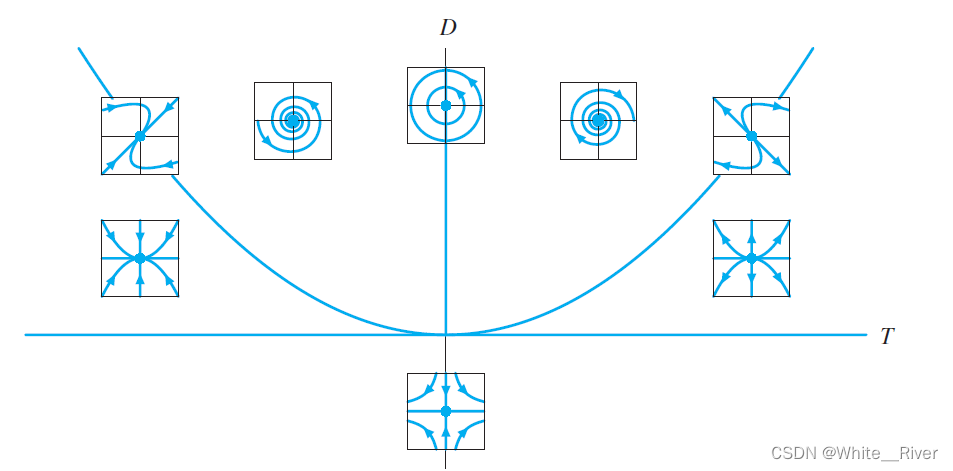
二阶系统的迹-行列式平面方法(trace-determinant methods for 2nd order system)
让我们再次考虑二阶线性系统 d Y d t = A Y \frac{d\mathbf{Y}}{dt}=A\mathbf{Y} dtdY=AY 我们已经知道,分析这种二阶系统。最主要的是注意它的特征值情形。 (此处没有重根的情形,所有是partial) 而特征值,也就是系统矩阵特征方程的根,和而系统矩阵是直接相关的。 我们知道,在线性代数理论中,矩阵A的迹Trace(A)(简称Tr)是A的