1. 引言 The non-adjacent form (NAF) of a number is a unique signed-digit representation. Like the name suggests, non-zero values cannot be adjacent. For example: ( 0 1 1 1 ) 2 = 4 + 2 + 1 = 7 (0\ 1\ 1

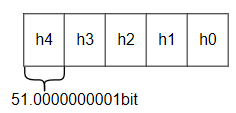
对于Curve25519，其Field域内的module Fp = 2255-19。 对于64位系统： /// A `FieldElement51` represents an element of the field/// \\( \mathbb Z / (2\^{255} - 19)\\).////// In the 64-bit implementation, a `FieldEle

1. 引言 Curve25519 Field Element在有限域 2 255 − 19 2^{255}-19 2255−19域内，采用64bit 串行计算时，采用的是5个FieldElement51元素来表示一个Element；若采用32-bit AVX2并行计算，则每个Element由10个FieldElement2526元素来表示。 即对于某Curve25519 Field Elemen

1. Curve25519定义 The Curve25519 function is Fp-restricted x-coordinate scalar multiplication on E(Fp2 ), where p is the prime number p = 2255 − 19 and E is the elliptic curve y2 = x3 + 486662x2 + x. 对

https://github.com/dalek-cryptography/curve25519-dalek 1. Scalar结构 针对p<2255的域filed，采用scalar以little-endian的数组形式来表示：【对于Curve25519，其p值为 2255 - 19】 /// The `Scalar` struct holds an integer \\(s < 2\^{2