dag专题

区块链有向无环图 DAG怎么用

区块链之所以能连成一条链，是因为新区块中有指向上一个区块的指针，所以说区块链的数据结构是一个链表。但是区块链的问题就在于它是一条线，假设一个区块生成的时间是固定的，那么这样一条线的结构就会造成性能瓶颈。因为每隔这个固定时间，只允许有一个区块添加到链上。所以要提升区块链的性能，大概有两个思路，一个是缩短生成一个区块的时间，而对于采用了 DAG 技术的区块链项目，走的就是另外一个思路了，

区块链 Fisco bcos 智能合约（19）-区块链性能腾飞：基于DAG的并行交易执行引擎PTE

在区块链世界中，交易是组成事务的基本单元。交易吞吐量很大程度上能限制或拓宽区块链业务的适用场景，愈高的吞吐量，意味着区块链能够支持愈广的适用范围和愈大的用户规模。当前，反映交易吞吐量的TPS（Transaction per Second，每秒交易数量）是评估性能的热点指标。为了提高TPS，业界提出了层出不穷的优化方案，殊途同归，各种优化手段的最终聚焦点，均是尽可能提高交易的并行处理能力

分片、侧链、状态通道、子链、DAG 是什么区别

一、分片(sharding) 区块链网络由主链和分片（shards）链组成，分片链上交易处于自己独立的空间中，可以独立处理交易。其核心思路是并非每个节点都需要处理所有的交易。分片之前整个网络的处理取决于单个节点的处理。分片后，只有同一片内的处理是同步的、一致的，不同分片之间则可以是异步的。这种属于底层解决方案，因为它是在区块链本身的基本协议中实施的。分片链的共

p2p、分布式，区块链笔记: Merkle-DAG和Merkle-Tree的区别与联系

Merkle-DAG和Merkle-Tree的区别与联系结构: Merkle-Tree 是一种二叉树结构，每个非叶子节点是其子节点哈希的哈希。它具有层次结构，通常用于验证数据的完整性。Merkle-DAG（有向无环图）是一种更通用的图结构，其一个节点可以有多个父节点和子节点。它允许更复杂的链接关系和非线性结构，适用于记录和追踪变更,支持广泛的并行操作和高效的增量更新。Merkle DAG 类

Codeforces Round #368 (Div. 2)（D. Persistent Bookcase 离线转化DAG）

题目链接给出n*m的书架，4种操作 1，x,y，如果(x,y)空，该位置则放一本书 2，x,y，如果(x,y)不空，该位置拿走一本书 3，x, 把这一层有书的拿出，没书的放上书，即反转 4，x, 返回到第x操作后的书架的状态初始书架是空的，要注意一点的是，题目可能在没书的地方拿书，有书的地方放书，明显这样的操作是不成功的，没影响的，所以要标记一下。麻烦的是第4操作，无法记录每次

训练赛 Grouping(强连通分量缩点 + DAG求最长路)

http://acm.sdut.edu.cn:8080/vjudge/contest/view.action?cid=158#problem/F 大致题意：给出n个人和m种关系(ti,si)，表示ti的年龄不小于si。问最小能被划分为几个集合，每个集合都要满足里面的人都无法比较。思路：对于一条路上的点，它们必定不能被划分到同一个集合中，因此原题变为求一条最长路。而题目中有可能出现

DAG计算框架：实现业务编排

文章目录 DAG如何实现DAG计算框架Node的实现Engine的实现Graph的实现具体某个节点如何使用在工作几年之后，大部分人如果还在继续做着 CRUD的简单重复工作，即使领导不提出对你更高的期望，自身也会感到焦虑吧。学如逆水行舟不进则退，年龄在增，技术深度也需要不断精进，否则就很可能面临淘汰。因此找个时间静下心来，为自己做一个技术规划是非常有必要的。在工作中想要做

在DAG（有向无环图）上的常见推论

1.DAG上某条边可能被经过的次数数量：通过在DAG上的总结，再结合我们在小学学过的乘法原理，我们可以考虑到一个规律：在一条边M（u->v）上，通过M的方法数量为从源点到达u的方式数量*从终点到达v的方式数量. 2.DAG上某个点可能被经过的次数数量：使用DP，并配合拓扑排序即可。

DAG（有向无环图）-入门基础

文章目录一、图基础1. 图2. 基础术语3. 有向图3. 有向无环图二、DAG算法基础1. 什么是DAG1. 图论算法——有向无环图三、参考一、图基础 1. 图图是数据结构中最为复杂的一种，图主要包括：无向图，结点的简单连接有向图，连接有方向性加权图，连接带有权值加权有向图，连接既有方向性，又带有权值图是由一组顶点和一组能够将两个顶点相连的边组成。

DAG最长路问题详解

DAG就是有向无环图，求解最长路，也就是所谓的关键路径。但是求解关键路径的方式比较复杂，而DAG上的最长路或者最短路问题又比较重要，很多问题都可以转换为求解DAG上的最长路或最短路问题。由于最长路和最短路的思想是一致的，因此下面以最长路为例：主要分为两个问题：（1）求整个DAG中的最长路径（即不固定起点和终点）（2）固定终点，求DAG的最长路径先解决第一个问题，给定一个有向无环图，

DAG图的拓扑排序 python

在DAG中DFS中顶点的出栈顺序即逆拓扑序。 def topological_sort( graph ):is_visit = dict( ( node, False ) for node in graph )li = []def dfs( graph, start_node ):for end_node in graph[start_node]:if not is_visit[

拓扑排序+有向无环图(DAG)的检测

参考: 算法导论第三版 p356, 数据结构与算法分析p218, 算法入门经典p110 拓扑排序的两张方法: 1.dfs搜索 2.模拟人工的拓扑两种方法的效率都是O(V + E) $$拓扑排序的方法也是有向无环图检测的方法 /*拓扑排序 dfs搜索 - 邻接表可以判断一个图是否有环*/#include <cstdio>#include <vector

区块链 | IPFS：Merkle DAG（进阶版）

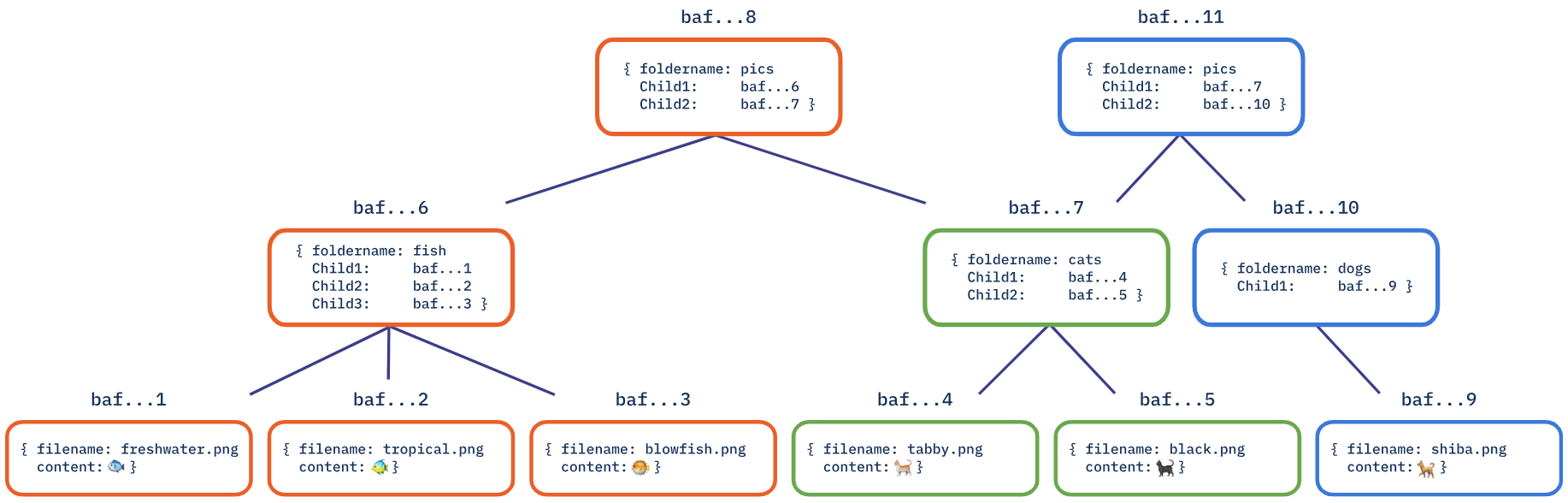
🦊原文：Merkle DAGs: Structuring Data for the Distributed Web 🦊写在前面：本文属于搬运博客，自己留存学习。 1 Merkle DAG 当我们在计算机上表示图时，必须通过提供节点和边的具体表示来编码我们的数据结构。由于 CID 可以唯一标识一个节点，因此我们可以使用 CID 来表示从一个节点到另一个节点的边。这样我们就创建了一种

区块链 | IPFS：Merkle DAG

🦊原文：IPFS: Merkle DAG 数据结构 - 知乎 🦊写在前面：本文属于搬运博客，自己留存学习。 1 Merkle DAG 的简介 Merkle DAG 是 IPFS 系统的核心概念之一。虽然 Merkle DAG 并不是由 IPFS 团队发明的，它来自于 Git 数据结构，但是 IPFS 团队对其进行了改造。可以肯定的是，IPFS 团队并非直接拿来使用，而是在原有基础上

RDD的依赖关系、窄依赖、宽依赖、RDD的缓存、RDD缓存方式、DAG的生成、RDD容错机制之Checkpoint

1、RDD的依赖关系 RDD和它依赖的父RDD（s）的关系有两种不同的类型，即窄依赖（narrow dependency）和宽依赖（wide dependency）。 1.1、窄依赖窄依赖指的是每一个父RDD的Partition最多被子RDD的一个Partition使用总结：窄依赖我们形象的比喻为独生子女 1.2、宽依赖宽依赖指的是多个子RDD的Partition会依赖同一

简介有向无环图DAG

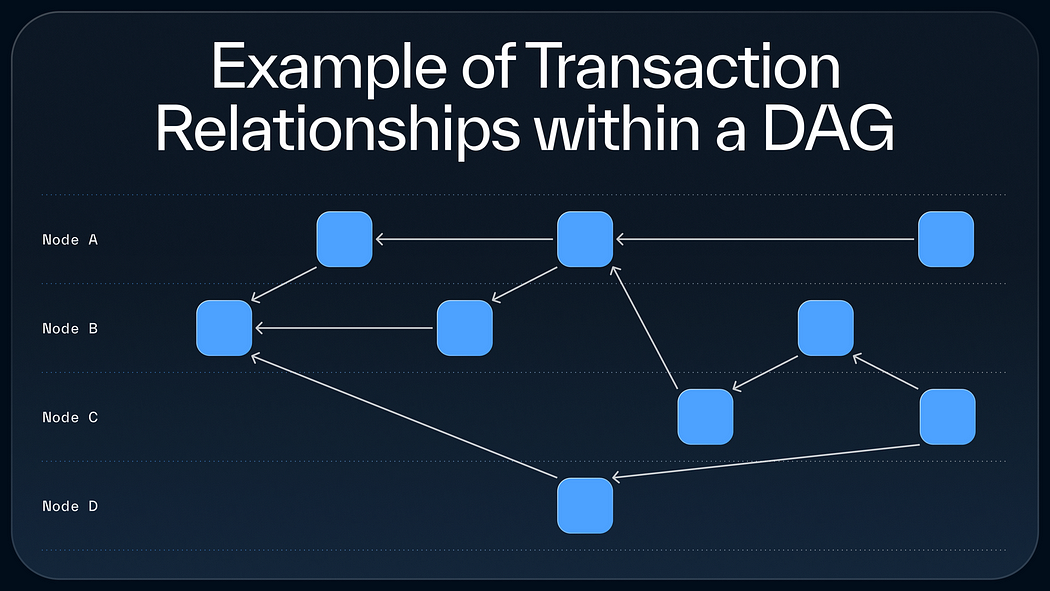
Sui创纪录的每秒交易量部分归功于数学构造，即有向无环图（Directed Acyclic Graph，DAG），该构造通过以最高效的方式处理交易来加速网络交易，而不是按照先来先服务的线性进展。区块链是设计用于确保数据完整性的分布式账本，将有向无环图的非线性特性与区块链相结合，是将两种技术的优点结合在一起。作为一个区块链网络，Sui保留了数据对象的历史性和监护性，而其基于DAG的共识系统使

区块链可扩展性的那些技术：侧链、分片、DAG ，子链！

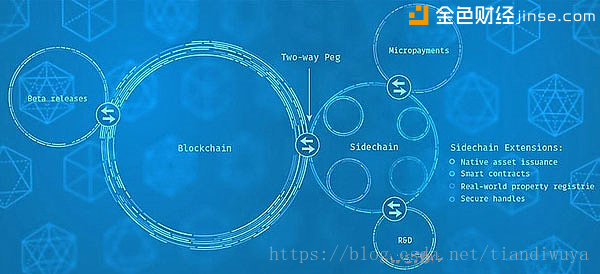
如果你经常浏览区块链相关的信息，你一定知道比特币交易开始变得拥堵，在社区中对于是扩容还是侧链的讨论喋喋不休。你肯定也知道就连以太坊也因《CryptoKitties》这款养猫游戏没能逃掉网络拥堵的命运。摆在我们面前的，是区块链技术发展到现在终会遇到的一个关键瓶颈——区块链（特别是公链）想要真正做到更深度化的应用和普及，关键就是要解决交易的吞吐量和交易的速度问题，这在区块链中也被称作”可扩展性“。

算法导论——24.2 DAG最短路径算法java实现

介绍 Bellman-Ford算法能在更普遍的情况下（存在负权边）解决单源点最短路径问题，但是对于DAG，可以有更加简化的算法去计算，使得时间复杂度更低。针对DAG的特点,以拓扑排序为基础,提出了解决DAG的最短路径问题的简单算法。通过理论分析,表明该算法具有理想的运算效率,其中,解决单源点问题的运算时间与E成正比,解决所有点对问题的运算时间与VE成正比。拓扑排序策略对于此类最短路径问题

Excahnge 2010之DAG配置

Excahnge 2010之DAG配置 1. 安装系统组件使用add-windowsfeature failover-clustering安装故障转移群集 2. 网络配置配置mapi 和copy 网络 Mapi 网络 MAPI 网络必须使用用于在 Intranet 内路由网络通信的子网或网络。确保选中“此连接使用下列项目”区域中的“Microsoft 网络客户端”、“In

Exchange 2010 之DAG安装

Exchange 2010 之DAG安装 1. 安装先决条件首先，我们来安装一下filter pack这个小软件再来安装一下必备的系统组件 Add-WindowsFeature NET-Framework,RSAT-ADDS,Web-Server,Web-Basic-Auth,Web-Windows-Auth,Web-Metabase,Web-Net-Ext,Web-Lgcy

学习区块链（十二）--DAG是真正的区块链3.0？别急！！！

首先，在我花了大量的时间来阅读DAG的相关文章和资料后，我仍然不敢确定我理解的DAG是正确的，我试图用最简单的话来描述DAG（有向无环图）以及它和区块链的区别。首先了解下数据结构中的有向无环图是什么？在图论中，图分为有向图和无向图两大类，在无向图中进一步进行约束形成了DAG（有向无环图），所谓无环是指它是由集合的顶点和有向边构成，每条边连接一个顶点到另一个，这样，假如顶点A开始，沿着有序的边，

最近在学习图相关的知识，在DAG中遇到一个未知的概念Source和Sink，然后我搜了一下国内的资源，好像没有关于该概念的讲解，最后我在stack overflow上找到了相关解答，先给出摘出的部分英文原文回答吧：By definition vertex with indegree 0 is called source and vertex with outdegree 0 is called s

271.【华为OD机试真题】查找一个有向网络的头节点和尾节点（有向无环图（DAG）-JavaPythonC++JS实现）

🚀点击这里可直接跳转到本专栏，可查阅顶置最新的华为OD机试宝典~ 本专栏所有题目均包含优质解题思路，高质量解题代码(Java&Python&C++&JS分别实现)，详细代码讲解，助你深入学习，深度掌握！文章目录一. 题目二.解题思路三.题解代码Python题解代码JAVA题解代码C/C++题解代码JS题解代码四.代码讲解(Java&Python&C++&JS分别讲解)

DAG上的动态规划——最长路CF4D Mysterious Present

CF4D Mysterious Present 用bool存储是否有边题目链接最长路例题像这种DAG上的最短路往往只需要记录是否存在边故可以用bool节省空间，该题用bool就可以过而用int就会MLE // Decline is inevitable// Romance will last forever#include <bits/stdc++.h>#de

学习区块链（十二）--DAG是真正的区块链3.0？别急！！！

首先，在我花了大量的时间来阅读DAG的相关文章和资料后，我仍然不敢确定我理解的DAG是正确的，我试图用最简单的话来描述DAG（有向无环图）以及它和区块链的区别。首先了解下数据结构中的有向无环图是什么？在图论中，图分为有向图和无向图两大类，在无向图中进一步进行约束形成了DAG（有向无环图），所谓无环是指它是由集合的顶点和有向边构成，每条边连接一个顶点到另一个，这样，假如顶点A开始，沿着有序的边，

UVA - 437（DAG模型）

一个盒子的高有三种状态，只要比较长和宽就行了。n个正方体可以看成n×3个矩形嵌套问题。可以转化成有向无环图，建完图后用记忆化搜索即可。状态转移方程：d(i) = max{d(j) + box[i].z} 代码： #include <cstdio>#include <cstring>#include <algorithm>using namespace std;const int max