cover专题
hdu5386(2015多校8)--Cover
题目链接:点击打开链接 题目大意:给出一个n*n的矩阵的初始值,和最终的值,现在有m个操作 L i j ,将第i列的值重置为j,H i j,将第i行的值重置为j。问m个操作应该怎么执行,可以完成矩阵的变化。 从最终的值向前找寻方案,每次找行和列中剩余的颜色全部相同的,看是否存在没被使用的操作可以完成它,如果有就记录下来,那么最终按照记录的逆序输出,就是可以完成变化的序列啦 #includ
Leetcode 3195. Find the Minimum Area to Cover All Ones I
Leetcode 3195. Find the Minimum Area to Cover All Ones I 1. 解题思路2. 代码实现 题目链接:3195. Find the Minimum Area to Cover All Ones I 1. 解题思路 这一题还是挺简单的,只要找到所有1所在的元素的上下左右4个边界,作为目标矩形的四个边即可。 2. 代码实现 给出python
hdu 5386 Cover(暴力)
题目链接:hdu 5386 Cover #include <cstdio>#include <cstring>#include <algorithm>using namespace std;const int maxn = 105;int N, M, G[maxn][maxn];int V[5 * maxn], H[maxn][maxn], L[maxn][maxn];void
Cover王锐大大——最长的一帧(第二日)
第一天我们走到了ViewerBase::frame()的viewerInit()这一步,第二天就继续来看看realize()这里做了什么工作。 当前位置:osgViewer/ViewerBase.h /** set up windows and associated threads.*/virtual void realize() = 0;又是一个纯虚函数,继续到Viewer里面去找。
GEE 10m 全球 LULC 数据集 ESRI Land Cover
土地利用土地覆盖(LULC)地图在许多行业部门和发展中国家越来越成为决策者的重要工具。这些地图提供的信息有助于通过更好地理解和量化地球过程和人类活动的影响,从而制定政策和土地管理决策。 ESRI Land Cover 数据介绍 ArcGIS Living Atlas of the World 提供了详细、准确且及时的全球 LULC 地图。该数据是 Esri 和 Impact
翻译《The Old New Thing》 - How do I cover the taskbar with a fullscreen window?
How do I cover the taskbar with a fullscreen window? - The Old New Thing (microsoft.com)https://devblogs.microsoft.com/oldnewthing/20050505-04/?p=35703 Raymond Chen 2005年5月5日 如何用全屏窗口覆盖任务栏?
HUST 1017 Exact cover(舞蹈链不能为了ac而ac)
题目链接:[kuangbin带你飞]专题三 Dancing Links A - Exact cover 题意 给定一01矩阵,问是否能够精确覆盖(就是选取任意行,这些行的1所在的列互不冲突且完整覆盖所有列),若有输出行号(要按递增顺序输出),否则输出NO。 思路 ps:两个礼拜前大略看了下舞蹈链(虽然英文名听起来更高端,但还是更喜欢它的中文名字),很精妙但也让人一看就惰性必生不愿再看
C. Cover the Tree2020 (dfs序构造) 牛客暑期多校训练营(第二场)
。 题意: 求最少的链覆盖所有边 思路: 可以想到任意链都得叶子开始叶子结尾,那么数目肯定是确定的,为叶子数目加一除以二。 可以想到,为了尽可能的覆盖更多变,我们要选宽度尽可能大的叶子相连。这里的宽度我们可以用dfs序表示,选择非叶子节点作为根然后求dfs序,然后两两配对。 但不能是最右边的叶子匹配最左边的叶子, 比如 1->2,1->3, 1->4 , 4->5, 4->6中,1->4边
微信小程序 cover-view 简单介绍/使用
cover-view:覆盖在原生组件之上的文本视图(可覆盖的原生组件包括 map、video、canvas、camera、live-player、live-pusher) 1、cover-view 只支持嵌套 cover-view、cover-image,可在 cover-view 中使用 button 2、cover-view 不支持设置单边的border、background-imag
cce2_空头回补cover_Takuri line_Inverted Hammer_Hanging Man_shooting star_double bottom_double top_Umbrel
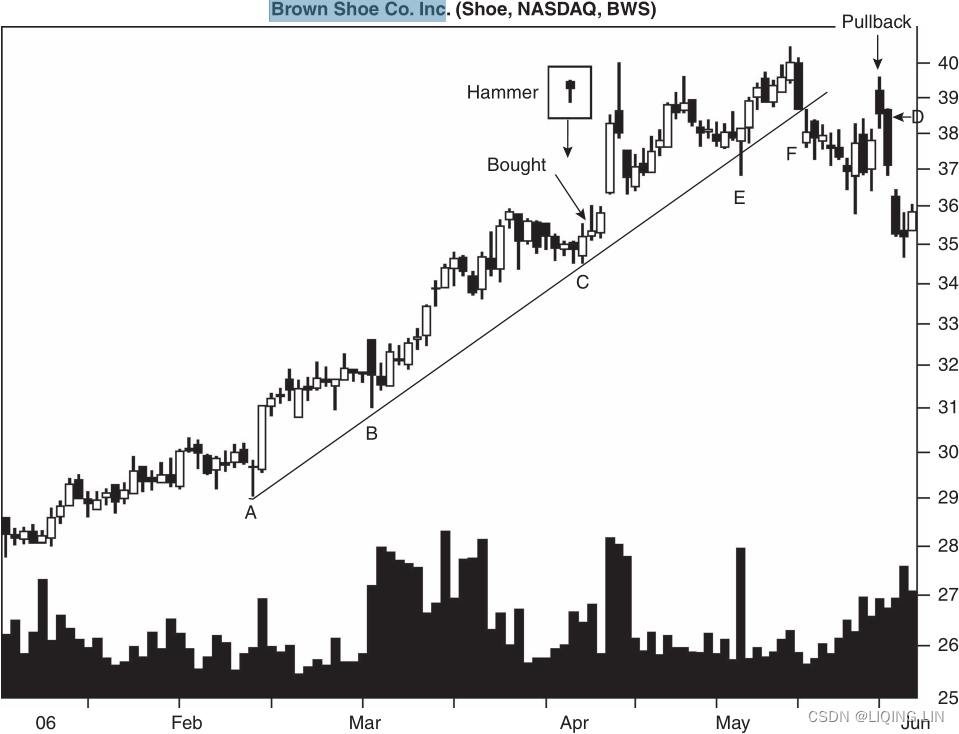
Umbrella Lines:Hanging Man and Hammer Like the previously mentioned candle lines, the Umbrella lines have strong reversal implications伞线具有强烈的反转含义. There is strong similarity between the Dragonfly Doj
2020牛客多校第二场C Cover the Tree(dfs序)
Cover the Tree (dfs序) 链接:https://ac.nowcoder.com/acm/contest/5667/C 来源:牛客网 题目大意: 给定一颗n个节点的无根树,任意两个结点(可叶子也可根节点)可形成一条链,让你用最少的链经过树上所有的边,然后输出这几条链的两边端点。 一开始看完这道题想的是要求树的直径,然后把未在直径的叶子节点两两配对,后来一想是错的,因为是要遍历
JS如何上传视频后从视频截图到一张封面Cover?
文章目录 概要获取上传视频文件截图小结 概要 从上传视频文件中获取一张图片 获取上传视频文件截图 html片段,两个都是隐藏的 <!--自定义的上传视频标签--><input type="file" style="display: none" id="file" ref="uploadVideo" accept="video/*"@change="uploadVi
PAT A1134 Vertex Cover ——悲欢离合总无情,一任阶前、点滴到天明
PAT A1134 Vertex Cover 判断所给集合中的点有没有cover到所有的边。在存储图的二维数组中,每个一维数组可以看作与某个顶点相关的所有边,所以当一个顶点出现时,就表示能cover到她的一维数组中的所有边so二维数组存储输入的图(边),再搞一个顶点的hash数组,之后开始判断,对于每个输入的集合,在hash数组中标记其中的点——每标记一个点就相当于划掉了二维数组中此顶点对应的一
2011百校联动“菜鸟杯”程序设计公开赛Cover The Enemy
今天下午又重新温习了菜鸟杯题,,发现好多题就是用枚举方法A掉的,,里面并没有夹杂太多方面的高级算法,,没想到就这题在比赛竟然好些做不出来,,看来自己做的题还是少啊!!!!! 思路:这一题求最小半径平方和,先把第一个塔离敌军的营地排一下序(升序,降序都可以),然后枚举所有到第一个塔的距离,通过找第一个塔不能覆盖的敌军阵营离第二个塔最大的距离得出第二个塔的半径,,还有一点要注意就是最找离第二个塔最
Set Cover的贪心算法
Set Cover的贪心算法 什么是Set Cover问题 SetCover问题即集合覆盖问题,给定一组集合,每个集合都有cost值,找到能够覆盖其中所有元素的一组集合,要求cost值总和最小。 具体思路 图源北航算法课件 目前关于集合覆盖问题,仍然找不到一个有效的OPT算法,我们这里提出的是一种基于贪心策略的近似性算法。 注意图中花写S和S的区别 我们每次选取的都是 c o
《学术英文写作》 如何和编辑套磁cover letter
The authors would like to extend their appreciation to Professor Yang for their helpful discussions and the Dear Eidter 写投稿信如何吸引Eidtor 英文单词没有书名号, 使用斜体。 第一段, 出现文章名, 期刊名 一边讲述一边评述 模板
大数据算法课程笔记5a: fixed-parameter vertex cover
1. 问题描述 一个vertex cover是一个点集的集合,并且保证图中的每一条边都存在至少一个顶点位于该点集中。 具体地, G=(V,E) G=(V,E) 的一个vertex cover S S满足 S⊆V∧{∀e=(v,w)∈E,v∈S or w∈S}S\subseteq V\wedge \{\forall e = (v,w)\in E, v\in S\text{ or } w\i
微信小程序ios中非cover组件点击重复触发地图tap事件
现象: map中使用view组件的@click事件会重复触发地图的@tap组件,只在ios上出现 <map id="maps" style="width: 100vw;height: 100vh;" :latitude="latitude" :longitude="longitude":markers="markers" show-location="true" :polyline="poly
1134. Vertex Cover (25)[图的遍历]
1. 原题: https://www.patest.cn/contests/pat-a-practise/1134 2. 思路 题意: 给出一个图,点的集合,判断图中所有边的至少一个点是否都包含在集合中。 思路: 图的遍历问题。 遍历每条边,看边的两点是否至少一点在集合里,否则输出no。 用了容器set。 3. 源码(已AC) #include <iostream>#i
CF 1900A Cover in Water 学习笔记
原题链接 传送门 题意 给定多个细胞,细胞有两种情况,一种情况是空的,另一种情况是阻塞的,可以往空的细胞里面装水,可以把装水细胞里面的水转移到另一个细胞里面,阻塞的细胞不能进行任何操作,如果一个空的细胞左右两边的细胞都有水,该细胞也会有水(大概类似于渗透作用),问需要多少水可以使得所有的空细胞里面装满水 代码 #include<bits/stdc++.h>using namespace
《代码/》(TFC2017主题曲|《成都》之程序员女声cover版) - 戴秋平
链接:https://i.y.qq.com/v8/playsong.html?songid=124902037&source=yqq#wechat_redirect 《代码/》(TFC2017主题曲|《成都》之程序员女声cover版) - 戴秋平 词:于涛 伴奏:网络 让我掉下眼泪的 不止内存泄漏 让我夜夜不眠的 不止你的需求 项目还要赶多久 你攥着我的手 让我感到为难的 是
ESA CCI land cover data土地利用数据下载
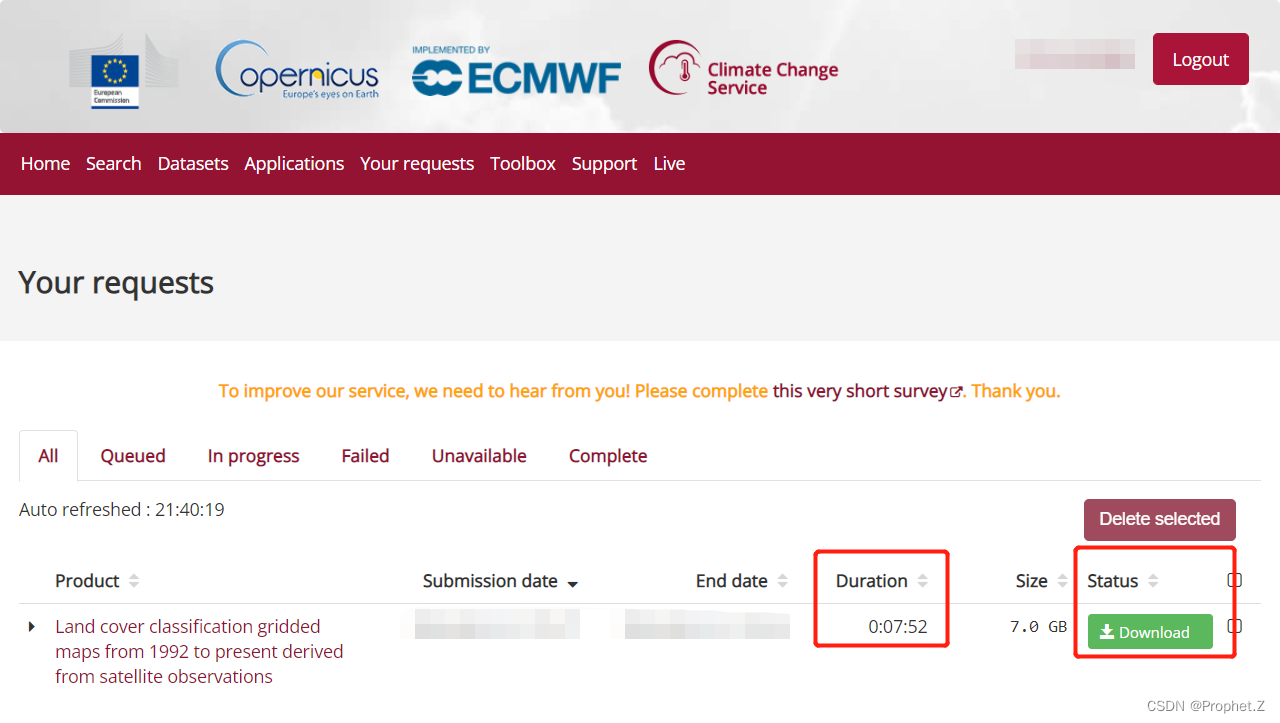
下载地址: https://cds.climate.copernicus.eu/cdsapp#!/dataset/satellite-land-cover?tab=overview 数据概况: 时间范围:1992-2020逐年数据空间分辨率:300m范围:全球数据格式:NetCDF4 数据下载: 选择年份,提交申请(需要先注册账号) 申请可能需要等待一段时间,也可能申请完立马通过,然
spoj1435 - Vertex Cover(贪心or树形dp)
暑期个人赛第二场 C - Vertex Cover 是uva10859简化版 题意: 找一个最小点集,使得每条边都能至少找到自己的一个端点, 这道题目前膜拜了两种方法,1-贪心 2-树形DP 贪心 思路:找出每个度为1的点a,找出它的唯一想相邻的节点b,则对于a和b之间的这条边而言,把b放到点集中是较优的决策。然后把点b及和b相连的边都删去,与b相邻节点的度数减1, 这样做是
PAT_甲级_1134 Vertex Cover (25point(s)) (C++)【散列】
目录 1,题目描述 题目大意 2,思路 3,AC代码 4,解题过程 第二搏 1,题目描述 vertex cover:顶点覆盖; 点集覆盖问题;incident:发生的事情(尤指不寻常的或讨厌的); 严重事件,暴力事件(如犯罪、事故、袭击等); (两国间的) 摩擦,冲突; (常指) 军事冲突; Sample Input: 10 118 76 84 58 48
解读澳洲嵌入式灯具防火等级 Non-IC Do-not-cover CA90 CA135 IC IC-4 具体要求。
以上标示相信大家都不陌生吧? 下面来介绍下澳洲嵌入灯具防火等级 等级划分: Non-IC Do-not-cover CA90 CA135 IC IC-4 定义诠释 Non-IC 不可安装在可燃物表面 安规符号: 测试条件: 1, 测试环境: 25℃±5℃ 2, 测试电压: 0.94 or 1.06 倍额定电压 3, 测试时间: 直到稳定或者8h以上 4, 测
uniapp小程序中给web-view页面添加授权弹窗(使用cover-view组件覆盖实现该功能)
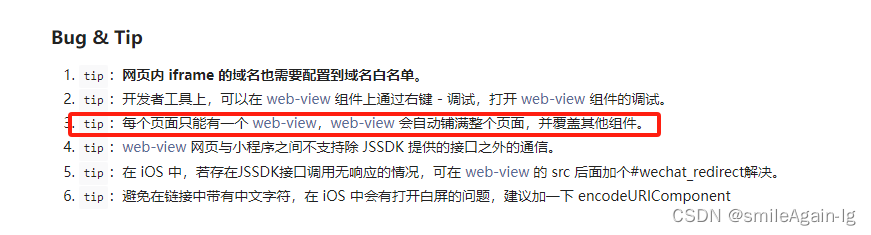
效果图: web-view是承载网页的容器。会自动铺满整个小程序页面,个人类型的小程序暂不支持使用。 再看下面一个提示: 每个页面只能有一个 web-view,web-view 会自动铺满整个页面,并覆盖其他组件。 也就是说,小程序中使用web-view打开网页,在页面上写的其它组件会直接被网页给覆盖住 需求:在web-view页面添加弹窗 刚好有一个组件cover-vi