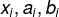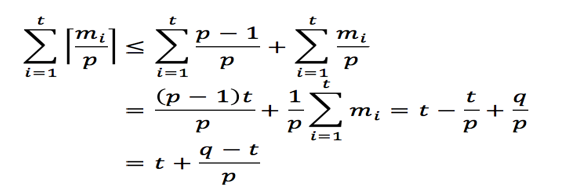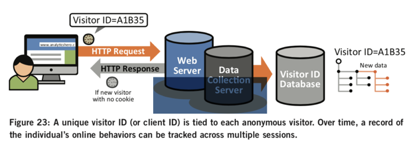
问题：用一个算法，实现判断是否会出现如下的有环的单链表 一、floyd 以龟兔赛跑来解释这一算法，寻找单链表中是否含有一个圈。 一、思想： 龟和兔子同时出发，龟走一步，兔子走两步，兔子比龟快，所以兔子一定可以追上龟，就好像在环形跑道中跑的快的运动员会从后面超过跑得慢的运动员。 //头指针给龟和兔，初始化tortoise = tophare = topforever://兔子走两

基础介绍： 给定给定区间，函数连续且，那么根据介值定理，函数必然在区间内有根。 二分法：将区间不断二分，使端点不断逼近零点。下一次迭代的区间为或，其中。割线法（线性插值）：基本思想是用弦的斜率近似代替目标函数的切线斜率，并用割线与横轴交点的横坐标作为方程式的根的近似。即给定两个点,。其割线方程为，那么令，x的值即为下一次迭代的结果。逆二次插值法：为割线法的进化版本。使用三个点确定一个二次函数，

Web Analytics 学习笔记—— Brent Dykes 《Web Analytic Kick Start》 Web AnalyticsWhy it matters?Web Analytics can provide insights into:Strategy always Comes First Must-Know Web MetricsPage ViewsRemark Visi

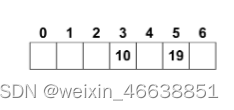
当我们用两个哈希函数的时候，探测的效率得到了提升，并且在一定程度上避免了聚集。 给出两个哈希函数 h1，h2 满足 h1，h2：K——> {0,1，...，m-1} Double hashing：设定h(k,i) = (h1(k) + ih2(k)) mod m    其中（i = 0,1,2，...，m-1）；m为表长 h2(k)的选择：每个值k的探测顺序必须达到所有位置0, . . .

1. 解方程（Solving Equations） 1.1 二分法（The Bisection Method） 定义1.1 对于方程 ，如果有 ，则说   是  的一个根。 定理1.2 令   是   上的连续函数，满足   , 则   在   和   之间存在一个根。 二分法算法流程： 二分法误差： 在区间  ，

1.参数解释： W(n)：在T(n)时间内，所有的工作负载 t(n)：并行算法所需要的总的时间 2.证明：