【算法】网络图中的dfs

2024-05-16 15:28
文章标签 算法 dfs 网络图

本文主要是介绍【算法】网络图中的dfs，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！



快乐的流畅：个人主页


个人专栏：《算法神殿》《数据结构世界》《进击的C++》

远方有一堆篝火，在为久候之人燃烧！

文章目录

  • 引言
  • 一、单词搜索
  • 二、黄金矿工
  • 三、不同路径 |||
  • 四、图像渲染
  • 五、岛屿数量
  • 六、岛屿的最大面积
  • 七、被围绕的区域
  • 八、太平洋大西洋水流问题
  • 九、扫雷游戏
  • 总结

引言

在二维网络图中的dfs，反而一般不需要画决策树，因为在二维图像中有时候很直观可以看出决策关系，一般为上下左右搜索。

一、单词搜索


细节：

  • dfs函数设置返回值bool，以便及时调整路线
  • 设置向量数组dx，dy
  • 设置bool数组vis，实现剪枝
  • pos设置为函数参数，方便回溯
class Solution
{int dx[4] = {1, -1, 0, 0};int dy[4] = {0, 0, 1, -1};bool vis[7][7];int m, n;
public:bool dfs(vector<vector<char>>& board, int i, int j, string& word, int pos){if(pos == word.size()) return true;vis[i][j] = true;for(int k=0; k<4; ++k){int x = i + dx[k], y = j + dy[k];if(x >= 0 && y >= 0 && x < m && y < n && !vis[x][y] && board[x][y] == word[pos]){if(dfs(board, x, y, word, pos + 1)) return true;}}vis[i][j] = false;return false;}bool exist(vector<vector<char>>& board, string& word){m = board.size(), n = board[0].size();for(int i=0; i<m; ++i){for(int j=0; j<n; ++j){if(board[i][j] == word[0]){if(dfs(board, i, j, word, 1)) return true;}}}return false;}
};

二、黄金矿工


细节：

  • 设置向量数组dx，dy
  • 设置bool数组vis，实现剪枝
  • sum设置为函数参数，方便回溯
class Solution
{int ret = 0;bool vis[16][16];int dx[4] = {1, -1, 0, 0};int dy[4] = {0, 0, 1, -1};int m, n;
public:void dfs(vector<vector<int>>& grid, int i, int j, int sum){vis[i][j] = true;for(int k=0; k<4; ++k){int x = i + dx[k], y = j + dy[k];if(x >= 0 && y >= 0 && x < m && y < n&& !vis[x][y] && grid[x][y]){dfs(grid, x, y, sum + grid[x][y]);}else ret = max(ret, sum);}vis[i][j] = false;}int getMaximumGold(vector<vector<int>>& grid){m = grid.size(), n = grid[0].size();for(int i=0; i<m; ++i){for(int j=0; j<n; ++j){if(grid[i][j]){dfs(grid, i, j, grid[i][j]);}}}return ret;}
};

三、不同路径 |||


细节：

  • 设置向量数组dx，dy
  • 设置bool数组vis，实现剪枝
  • path设置为函数参数，方便回溯
class Solution
{int ret = 0;int dx[4] = {1, -1, 0, 0};int dy[4] = {0, 0, 1, -1};bool vis[20][20];int m, n, count = 0;
public:void dfs(vector<vector<int>>& grid, int i, int j, int path){if(grid[i][j] == 2){if(path + count == m * n) ++ret;return;}vis[i][j] = true;for(int k=0; k<4; ++k){int x = i + dx[k], y = j + dy[k];if(x >= 0 && y >= 0 && x < m && y < n&& !vis[x][y] && grid[x][y] != -1){dfs(grid, x, y, path + 1);}}vis[i][j] = false;}int uniquePathsIII(vector<vector<int>>& grid){m = grid.size(), n = grid[0].size();int si, sj;for(int i=0; i<m; ++i){for(int j=0; j<n; ++j){if(grid[i][j] == -1) ++count;else if(grid[i][j] == 1) {si = i, sj = j;}}}dfs(grid, si, sj, 1);return ret;}
};
  • 本题开始往后，是floodfill算法的练习
  • floodfill算法，本质就是寻找连通块
  • 同时floodfill算法没有回溯

四、图像渲染



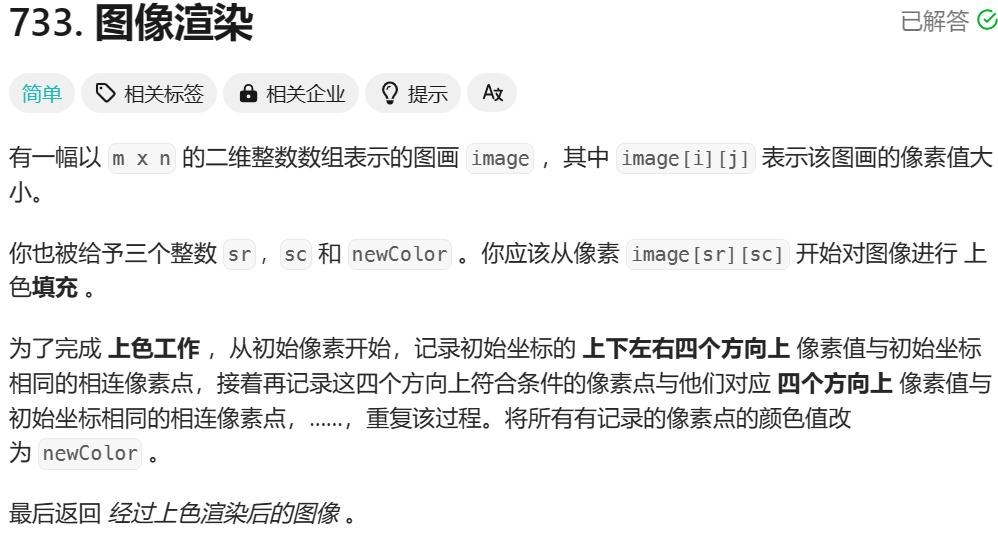
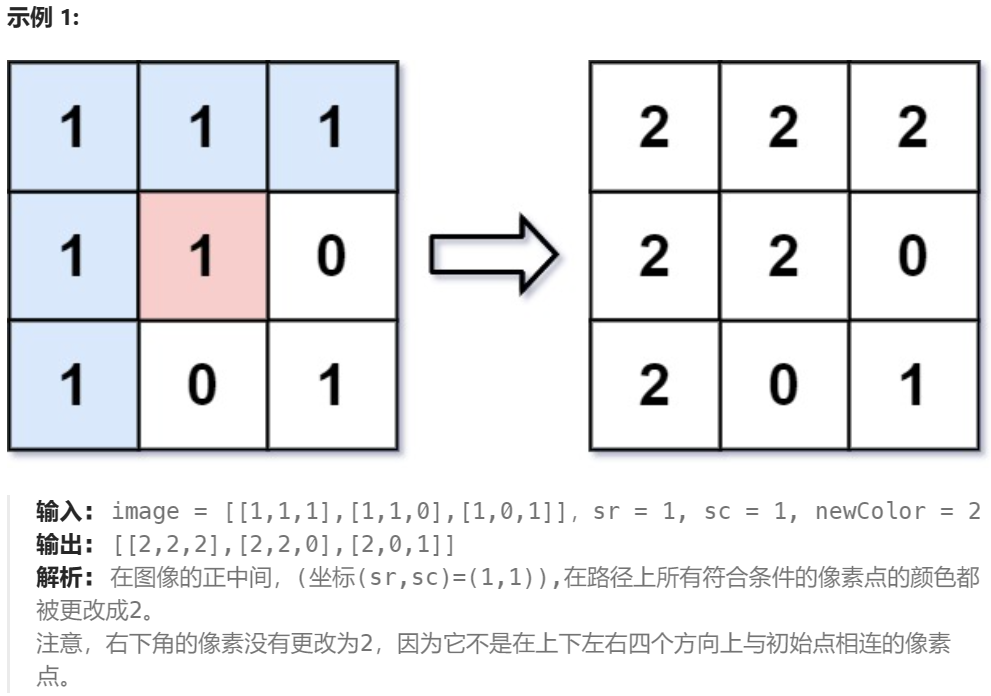
细节：

  • 设置向量数组dx，dy
  • 记录baseColor, newColor
class Solution
{int dx[4] = {1, -1, 0, 0};int dy[4] = {0, 0, 1, -1};int baseColor, newColor;int m, n;
public:void dfs(vector<vector<int>>& image, int i, int j){image[i][j] = newColor;for(int k=0; k<4; ++k){int x = i + dx[k], y = j + dy[k];if(x >= 0 && y >= 0 && x < m && y < n && image[x][y] == baseColor){dfs(image, x, y);}}}vector<vector<int>> floodFill(vector<vector<int>>& image, int sr, int sc, int color){if(image[sr][sc] == color) return image;baseColor = image[sr][sc], newColor = color;m = image.size(), n = image[0].size();dfs(image, sr, sc);return image;}
};

五、岛屿数量


细节：

  • 设置向量数组dx，dy
  • 设置bool数组vis，实现剪枝
class Solution
{int ret;bool vis[301][301];int dx[4] = {1, -1, 0, 0};int dy[4] = {0, 0, 1, -1};int m, n;
public:void dfs(vector<vector<char>>& grid, int i, int j){vis[i][j] = true;for(int k=0; k<4; ++k){int x = i + dx[k], y = j + dy[k];if(x >= 0 && y >= 0 && x < m && y < n&& !vis[x][y] && grid[x][y] == '1'){dfs(grid, x, y);}}}int numIslands(vector<vector<char>>& grid){m = grid.size(), n = grid[0].size();for(int i=0; i<m; ++i){for(int j=0; j<n; ++j){if(!vis[i][j] && grid[i][j] == '1'){dfs(grid, i, j);++ret;}}}return ret;}
};

六、岛屿的最大面积



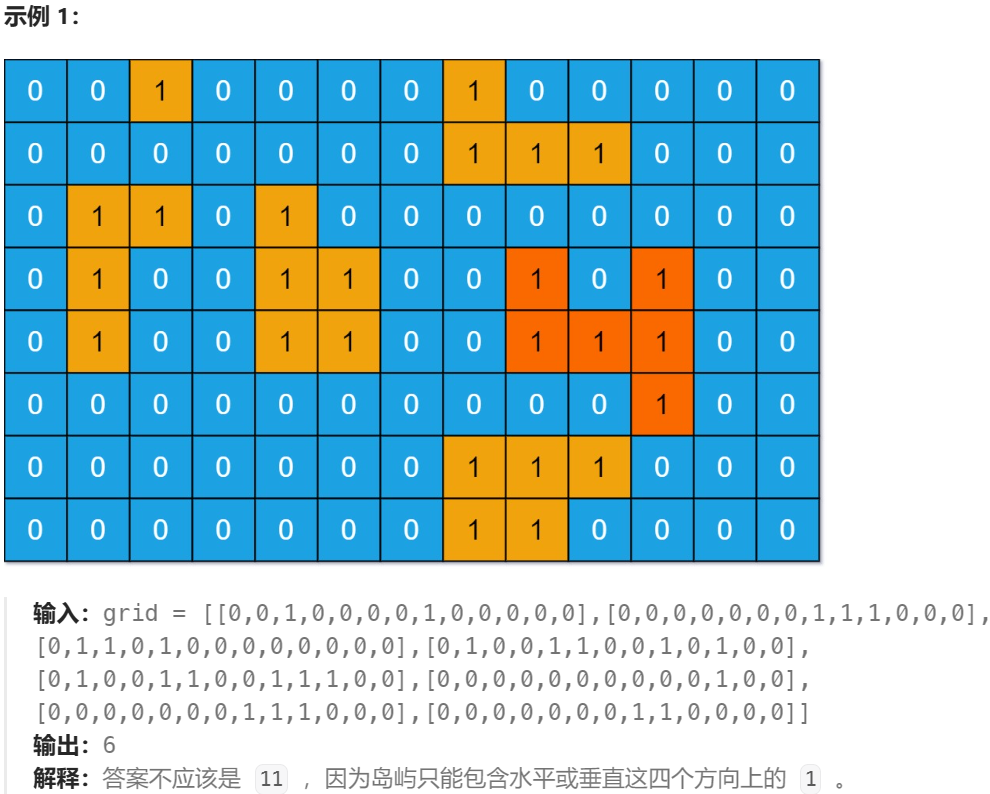
细节：

  • 设置向量数组dx，dy
  • 设置bool数组vis，实现剪枝
class Solution
{int ret, sum;vector<vector<bool>> vis;int dx[4] = {1, -1, 0, 0};int dy[4] = {0, 0, 1, -1};int m, n;
public:void dfs(vector<vector<int>>& grid, int i, int j){++sum;vis[i][j] = true;for(int k=0; k<4; ++k){int x = i + dx[k], y = j + dy[k];if(x >= 0 && y >= 0 && x < m && y < n&& !vis[x][y] && grid[x][y] == 1){dfs(grid, x, y);}else ret = max(ret, sum);}}int maxAreaOfIsland(vector<vector<int>>& grid){m = grid.size(), n = grid[0].size();vis.resize(m, vector<bool>(n));for(int i=0; i<m; ++i){for(int j=0; j<n; ++j){if(!vis[i][j] && grid[i][j] == 1){sum = 0;dfs(grid, i, j);}}}return ret;}
};

七、被围绕的区域


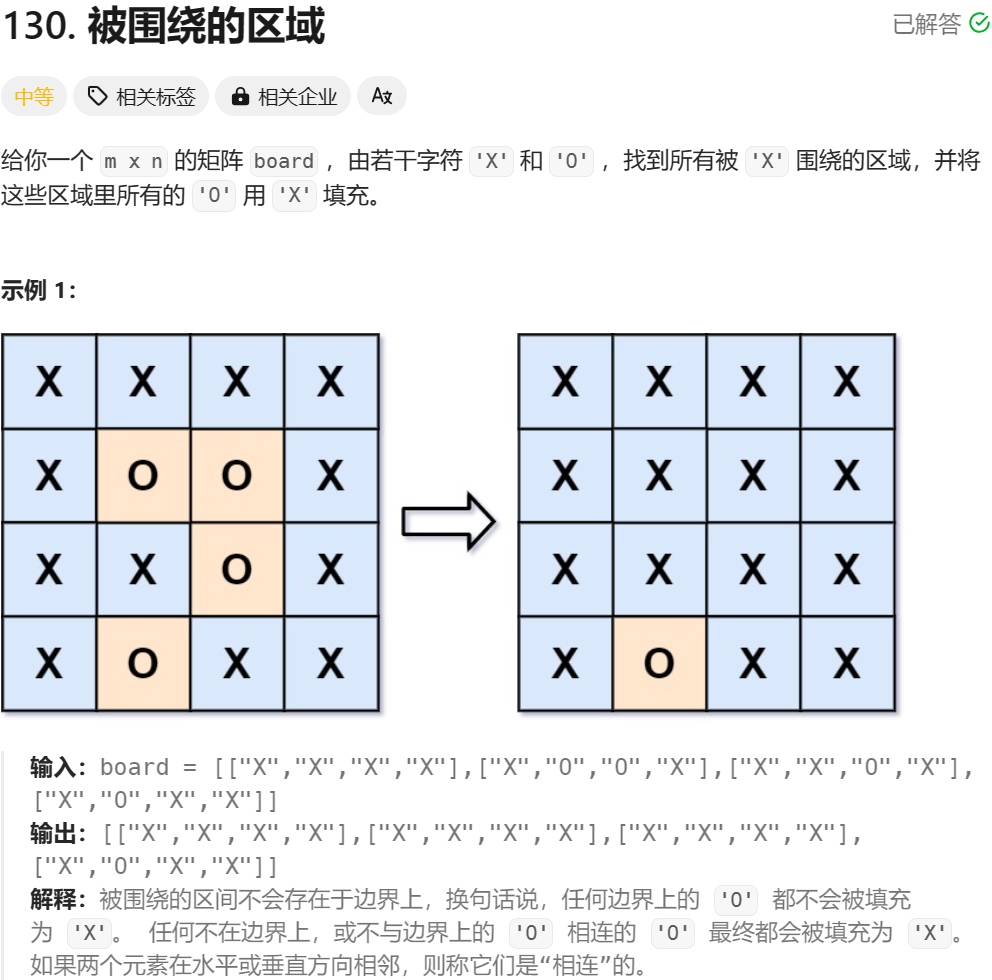
细节：

  • 正难则反，将边界上及其相连的‘O’先全部标记起来，最后遍历矩阵，将未被标记的‘O’改成‘X’
  • 设置向量数组dx，dy
  • 设置bool数组vis，实现剪枝
class Solution
{vector<vector<bool>> vis;int dx[4] = {1, -1, 0, 0};int dy[4] = {0, 0, 1, -1};int m, n;
public:void dfs(vector<vector<char>>& board, int i, int j){vis[i][j] = true;for(int k=0; k<4; ++k){int x = i + dx[k], y = j + dy[k];if(x >= 0 && y >= 0 && x < m && y < n&& !vis[x][y] && board[x][y] == 'O'){dfs(board, x, y);}}}void solve(vector<vector<char>>& board){m = board.size(), n = board[0].size();vis.resize(m, vector<bool>(n));for(int i=0; i<m; ++i){if(board[i][0] == 'O') dfs(board, i, 0);if(board[i][n-1] == 'O') dfs(board, i, n-1);}for(int j=0; j<n; ++j){if(board[0][j] == 'O') dfs(board, 0, j);if(board[m-1][j] == 'O') dfs(board, m-1, j);}for(int i=0; i<m; ++i){for(int j=0; j<n; ++j){if(!vis[i][j] && board[i][j] == 'O'){board[i][j] = 'X';}}}}
};

八、太平洋大西洋水流问题




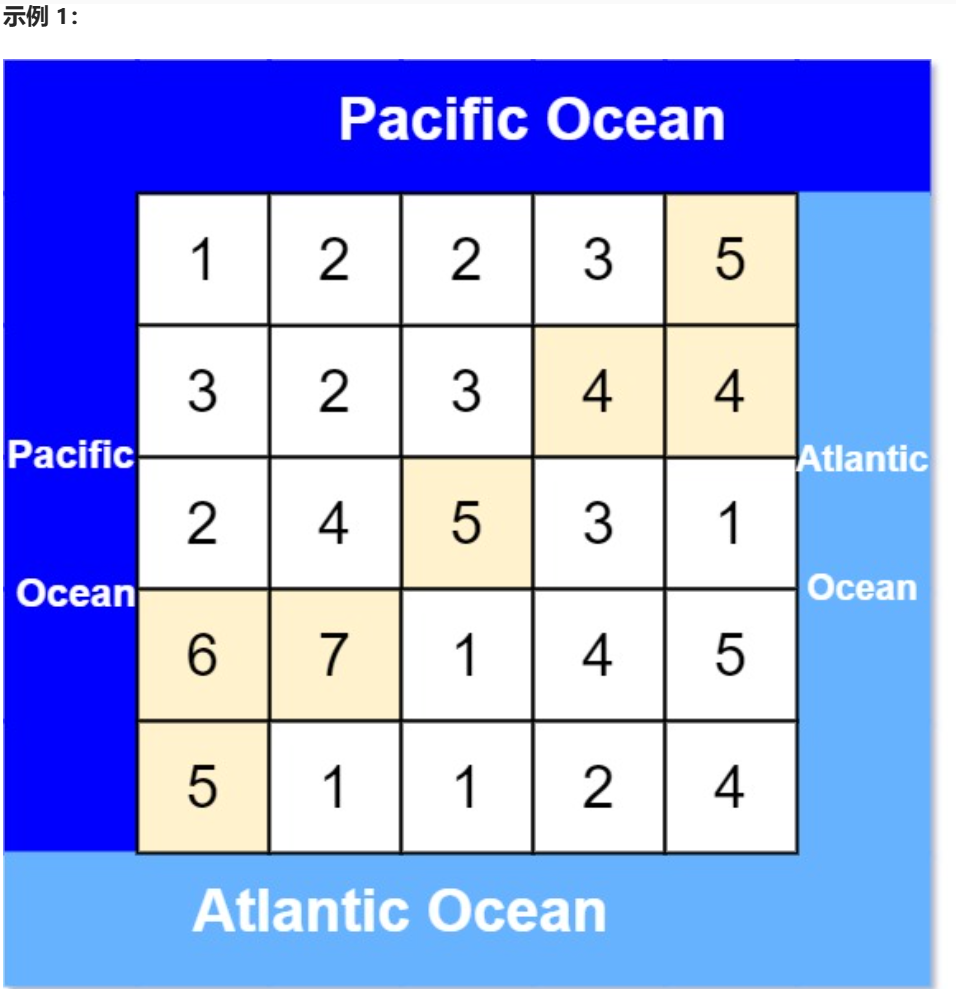
思路：正难则反，水往高处流。

  • 利用两个标记数组，分别记录太平洋和大西洋的水可以流到的区域，找出标记数组重叠的部分即可。
  • 为了只用写一份dfs函数，将vis标记数组以参数的形式传递
  • 设置向量数组dx，dy
class Solution
{int dx[4] = {1, -1, 0, 0};int dy[4] = {0, 0, 1, -1};int m, n;
public:void dfs(vector<vector<int>>& heights, int i, int j, vector<vector<bool>>& vis){vis[i][j] = true;for(int k=0; k<4; ++k){int x = i + dx[k], y = j + dy[k];if(x >= 0 && y >= 0 && x < m && y < n&& !vis[x][y] && heights[x][y] >= heights[i][j])//正难则反，水往高处流{dfs(heights, x, y, vis);}}}vector<vector<int>> pacificAtlantic(vector<vector<int>>& heights){m = heights.size(), n = heights[0].size();vector<vector<bool>> vis1(m, vector<bool>(n));vector<vector<bool>> vis2(m, vector<bool>(n));for(int i=0; i<m; ++i){if(!vis1[i][0]) dfs(heights, i, 0, vis1);if(!vis2[i][n-1]) dfs(heights, i, n-1, vis2);}for(int j=0; j<n; ++j){if(!vis1[0][j]) dfs(heights, 0, j, vis1);if(!vis2[m-1][j]) dfs(heights, m-1, j, vis2);}vector<vector<int>> ret;for(int i=0; i<m; ++i){for(int j=0; j<n; ++j){if(vis1[i][j] && vis2[i][j]){ret.push_back({i, j});}}}return ret;}
};

九、扫雷游戏



细节：本题实际上是一道模拟题，关键是理解题意。

  • 点击位置是雷，直接改变返回
  • 不是雷，则进入dfs函数递归
  • 对于当前格子，先计算周围8个格子中雷的数量
    • 如果有雷，将当前格子改为雷的数量，返回
    • 如果无雷，将当前格子改为挖出的空方块，继续递归
  • 递归的时候，要进行8个方向的搜索，所以向量数组要存储8个方向
class Solution
{bool vis[51][51];int dx[8] = {1, 1, 1, 0, 0, -1, -1, -1};int dy[8] = {1, 0, -1, 1, -1, 1, 0, -1};int m, n;
public:void dfs(vector<vector<char>>& board, int i, int j){if(board[i][j] == 'M') return;int count = 0;for(int k=0; k<8; ++k){int x = i + dx[k], y = j + dy[k];if(x >= 0 && y >= 0 && x < m && y < n && board[x][y] == 'M'){++count;}}if(count){board[i][j] = count + '0';return;}else board[i][j] = 'B';vis[i][j] = true;for(int k=0; k<8; ++k){int x = i + dx[k], y = j + dy[k];if(x >= 0 && y >= 0 && x < m && y < n && !vis[x][y]){dfs(board, x, y);}}}vector<vector<char>> updateBoard(vector<vector<char>>& board, vector<int>& click){int ci = click[0], cj = click[1];if(board[ci][cj] == 'M'){board[ci][cj] = 'X';return board;}m = board.size(), n = board[0].size();dfs(board, ci, cj);return board;}
};

总结

网络图中的dfs，常用的搜索技巧，是创建向量数组dx，dy，方便简洁地用循环遍历。


真诚点赞，手有余香

这篇关于【算法】网络图中的dfs的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！


http://www.chinasem.cn/article/995294。

相关文章

不懂推荐算法也能设计推荐系统

不懂推荐算法也能设计推荐系统

本文以商业化应用推荐为例，告诉我们不懂推荐算法的产品，也能从产品侧出发， 设计出一款不错的推荐系统。 相信很多新手产品，看到算法二字，多是懵圈的。 什么排序算法、最短路径等都是相对传统的算法（注：传统是指科班出身的产品都会接触过）。但对于推荐算法，多数产品对着网上搜到的资源，都会无从下手。特别当某些推荐算法 和 “AI”扯上关系后，更是加大了理解的难度。 但，不了解推荐算法，就无法做推荐系
阅读更多...
康拓展开（hash算法中会用到）

康拓展开（hash算法中会用到）

康拓展开是一个全排列到一个自然数的双射（也就是某个全排列与某个自然数一一对应） 公式： X=a[n]*(n-1)!+a[n-1]*(n-2)!+...+a[i]*(i-1)!+...+a[1]*0! 其中,a[i]为整数,并且0<=a[i]<i,1<=i<=n。（a[i]在不同应用中的含义不同）； 典型应用： 计算当前排列在所有由小到大全排列中的顺序，也就是说求当前排列是第
阅读更多...
csu 1446 Problem J Modified LCS （扩展欧几里得算法的简单应用）

csu 1446 Problem J Modified LCS （扩展欧几里得算法的简单应用）

这是一道扩展欧几里得算法的简单应用题，这题是在湖南多校训练赛中队友ac的一道题，在比赛之后请教了队友，然后自己把它a掉 这也是自己独自做扩展欧几里得算法的题目 题意：把题意转变下就变成了：求d1*x - d2*y = f2 - f1的解,很明显用exgcd来解 下面介绍一下exgcd的一些知识点：求ax + by = c的解 一、首先求ax + by = gcd(a,b)的解 这个
阅读更多...
综合安防管理平台LntonAIServer视频监控汇聚抖动检测算法优势

综合安防管理平台LntonAIServer视频监控汇聚抖动检测算法优势

LntonAIServer视频质量诊断功能中的抖动检测是一个专门针对视频稳定性进行分析的功能。抖动通常是指视频帧之间的不必要运动，这种运动可能是由于摄像机的移动、传输中的错误或编解码问题导致的。抖动检测对于确保视频内容的平滑性和观看体验至关重要。 优势 1. 提高图像质量 - 清晰度提升：减少抖动，提高图像的清晰度和细节表现力，使得监控画面更加真实可信。 - 细节增强：在低光条件下，抖
阅读更多...
【数据结构】——原来排序算法搞懂这些就行，轻松拿捏

【数据结构】——原来排序算法搞懂这些就行，轻松拿捏

前言：快速排序的实现最重要的是找基准值，下面让我们来了解如何实现找基准值 基准值的注释：在快排的过程中，每一次我们要取一个元素作为枢纽值，以这个数字来将序列划分为两部分。 在此我们采用三数取中法，也就是取左端、中间、右端三个数，然后进行排序，将中间数作为枢纽值。 快速排序实现主框架： //快速排序 void QuickSort(int* arr, int left, int rig
阅读更多...
poj 3974 and hdu 3068 最长回文串的O（n）解法(Manacher算法)

poj 3974 and hdu 3068 最长回文串的O（n）解法(Manacher算法)

求一段字符串中的最长回文串。 因为数据量比较大，用原来的O（n^2）会爆。 小白上的O(n^2)解法代码：TLE啦~ #include<stdio.h>#include<string.h>const int Maxn = 1000000;char s[Maxn];int main(){char e[] = {"END"};while(scanf("%s", s) != EO
阅读更多...
秋招最新大模型算法面试，熬夜都要肝完它

秋招最新大模型算法面试，熬夜都要肝完它

💥大家在面试大模型LLM这个板块的时候，不知道面试完会不会复盘、总结，做笔记的习惯，这份大模型算法岗面试八股笔记也帮助不少人拿到过offer ✨对于面试大模型算法工程师会有一定的帮助，都附有完整答案，熬夜也要看完，祝大家一臂之力 这份《大模型算法工程师面试题》已经上传CSDN，还有完整版的大模型 AI 学习资料，朋友们如果需要可以微信扫描下方CSDN官方认证二维码免费领取【保证100%免费
阅读更多...
hdu 2489 (dfs枚举 + prim)

hdu 2489 (dfs枚举 + prim)

题意： 对于一棵顶点和边都有权值的树，使用下面的等式来计算Ratio 给定一个n 个顶点的完全图及它所有顶点和边的权值，找到一个该图含有m 个顶点的子图，并且让这个子图的Ratio 值在所有m 个顶点的树中最小。 解析： 因为数据量不大，先用dfs枚举搭配出m个子节点，算出点和，然后套个prim算出边和，每次比较大小即可。 dfs没有写好，A的老泪纵横。 错在把index在d
阅读更多...
poj 3050 dfs + set的妙用

poj 3050 dfs + set的妙用

题意: 给一个5x5的矩阵，求由多少个由连续6个元素组成的不一样的字符的个数。 解析： dfs + set去重搞定。 代码： #include <iostream>#include <cstdio>#include <set>#include <cstdlib>#include <algorithm>#include <cstring>#include <cm
阅读更多...
dp算法练习题【8】

dp算法练习题【8】

不同二叉搜索树 96. 不同的二叉搜索树 给你一个整数 n ，求恰由 n 个节点组成且节点值从 1 到 n 互不相同的 二叉搜索树 有多少种？返回满足题意的二叉搜索树的种数。 示例 1： 输入：n = 3输出：5 示例 2： 输入：n = 1输出：1 class Solution {public int numTrees(int n) {int[] dp = new int
阅读更多...

Copyright China编程 23002807@qq.com

沪ICP备2023033072号-2