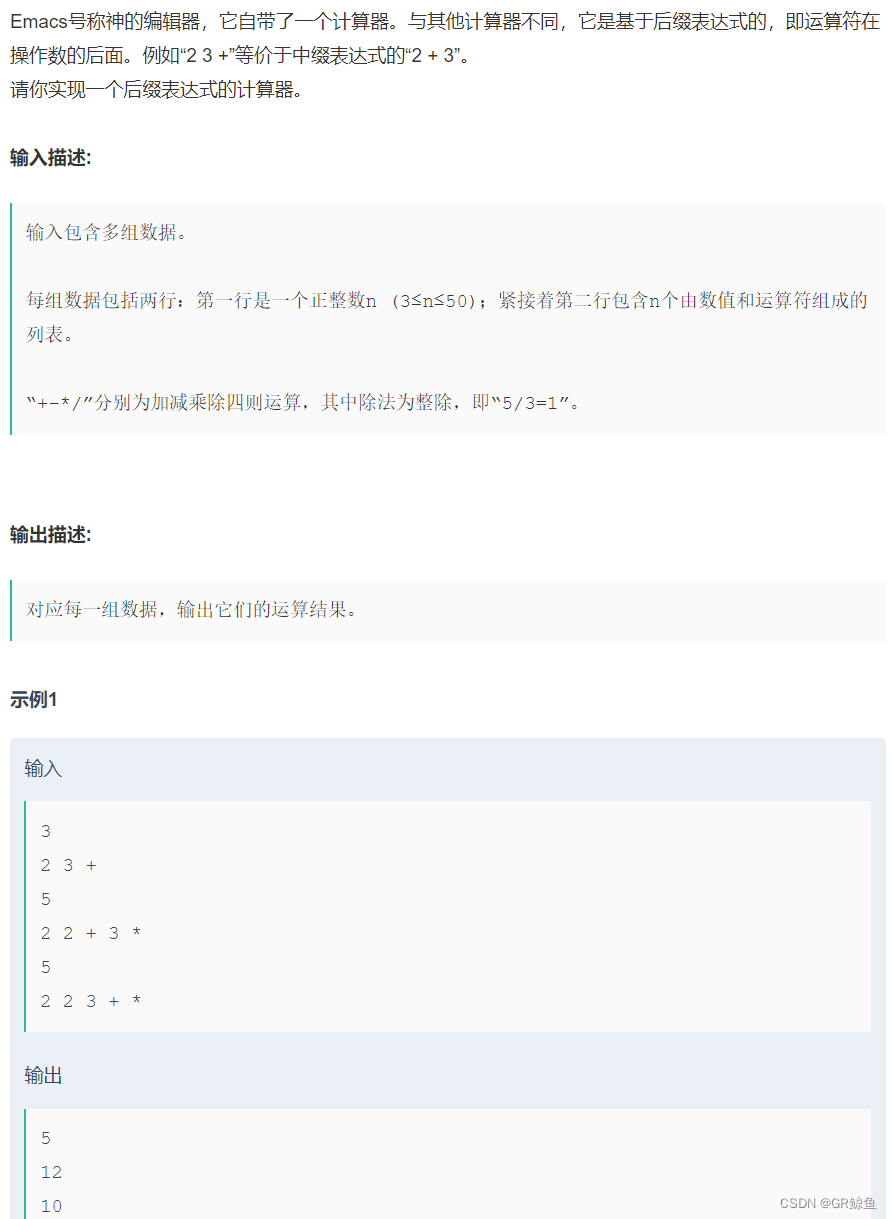
本文主要是介绍MT3035 逆波兰式,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!


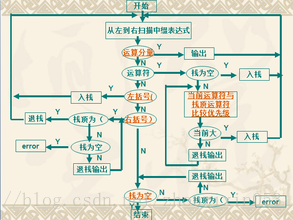
思路:
两个栈str1和sr2,分别存放运算符和结果。
如果是数字,直接放入str2中。
如果是运算符:
1. ( :直接放入 str1
2. +/-/*// 看栈顶元素,若当前字符优先级比栈顶大,则压到str1中;否则str1中元素出栈压到str2中直到当前字符优先级比栈顶大,再把当前字符压到str1中。
3. ) :str1元素依次出栈压到str2中,直到碰见( 。
例子:8-(3+2*6)/5+4
str1: str2: 8
str1:- str2: 8
str1:- ( str2: 8
str1:- ( str2: 8 3
str1:- ( + str2: 8 3
str1:- ( + str2: 8 3 2
str1:- ( + * str2: 8 3 2
str1:- ( + * str2: 8 3 2 6
此时遇见):
str1:- str2: 8 3 2 6 * +
str1:- / str2: 8 3 2 6 * +
str1:- / str2: 8 3 2 6 * + 5
此时遇见+,因为str1栈顶为/,所以要把/放到str2;str1栈顶此时为-,因为+不比-优先级高,所以-也放入str2中:
str1: + str2: 8 3 2 6 * + 5 / -
str1: + str2: 8 3 2 6 * + 5 / - 4
最后把str1中元素依次压到str2中:
str1: str2: 8 3 2 6 * + 5 / - 4 +
所以最后str2中元素逆序出栈即为逆波兰式。
代码:
#include <bits/stdc++.h>
using namespace std;
#define ll long long
const int N = 1e6 + 10;
bool is_op(char c)
{return c == '+' || c == '-' || c == '*' || c == '/';
}
int prority(char op)
{if (op == '+' || op == '-')return 1;if (op == '*' || op == '/')return 2;return -1;
}
void process_op(string s)
{ // 后缀表达式的求值stack<int> st;bool change = false; // 记录是否需要打印for (int i = 0; i < s.length(); i++){if (is_op(s[i])){int r = st.top();st.pop();int l = st.top();st.pop();switch (s[i]){case '+':st.push(l + r);break;case '-':st.push(l - r);break;case '*':st.push(l * r);break;case '/':st.push(l / r);break;}change = true; // 计算,需要打印}else{st.push(s[i] - '0'); // 数字入栈change = false; // 不需打印}if (change){ // 打印后缀表达式stack<int> temp1, temp2;temp1 = st;while (!temp1.empty()){ // 将栈中元素倒序temp2.push(temp1.top());temp1.pop();}while (!temp2.empty()){ // 打印计算的前半段cout << temp2.top() << " ";temp2.pop();}for (int j = i + 1; j < s.length(); j++){ // 打印未计算的后半段cout << s[j] << " ";}cout << endl;}}
}
string toRPN(string s)
{ // 中缀转后缀stack<char> st; // 结果栈stack<char> op; // 操作数栈for (int i = 0; i < s.size(); i++){if (s[i] == '('){op.push(s[i]);}else if (s[i] == ')'){while (op.top() != '('){st.push(op.top());op.pop();}op.pop(); // 弹出'('}else if (is_op(s[i])){while (!op.empty() && prority(op.top()) >= prority(s[i])){ // 当前符号不比栈顶符号优先级高st.push(op.top());op.pop();}op.push(s[i]);}else // 数字{st.push(s[i]);}}while (!op.empty()){ // 最后把op中的符号全部弹出压入stst.push(op.top());op.pop();}// 逆序放到ans中string ans;int len = st.size();while (len--){ans = st.top() + ans;st.pop();}return ans;
}
int main()
{string s;cin >> s;string s2 = toRPN(s); // 存放逆波兰式for (int i = 0; i < s2.length(); i++){cout << s2[i] << " ";}cout << endl;process_op(s2);return 0;
}这篇关于MT3035 逆波兰式的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!