算法学习笔记（5.0）-基于比较的高效排序算法-归并排序

本文主要是介绍算法学习笔记（5.0）-基于比较的高效排序算法-归并排序，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

##时间复杂度O(nlogn)

目录

##时间复杂度O(nlogn)

##递归实现归并排序

##原理

##图例

##代码实现

##非递归实现归并排序

##释

#代码实现

---

##递归实现归并排序

##原理

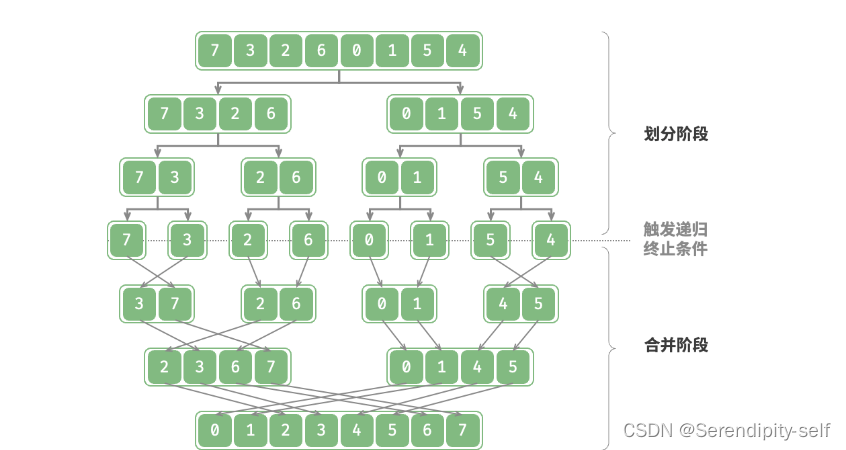
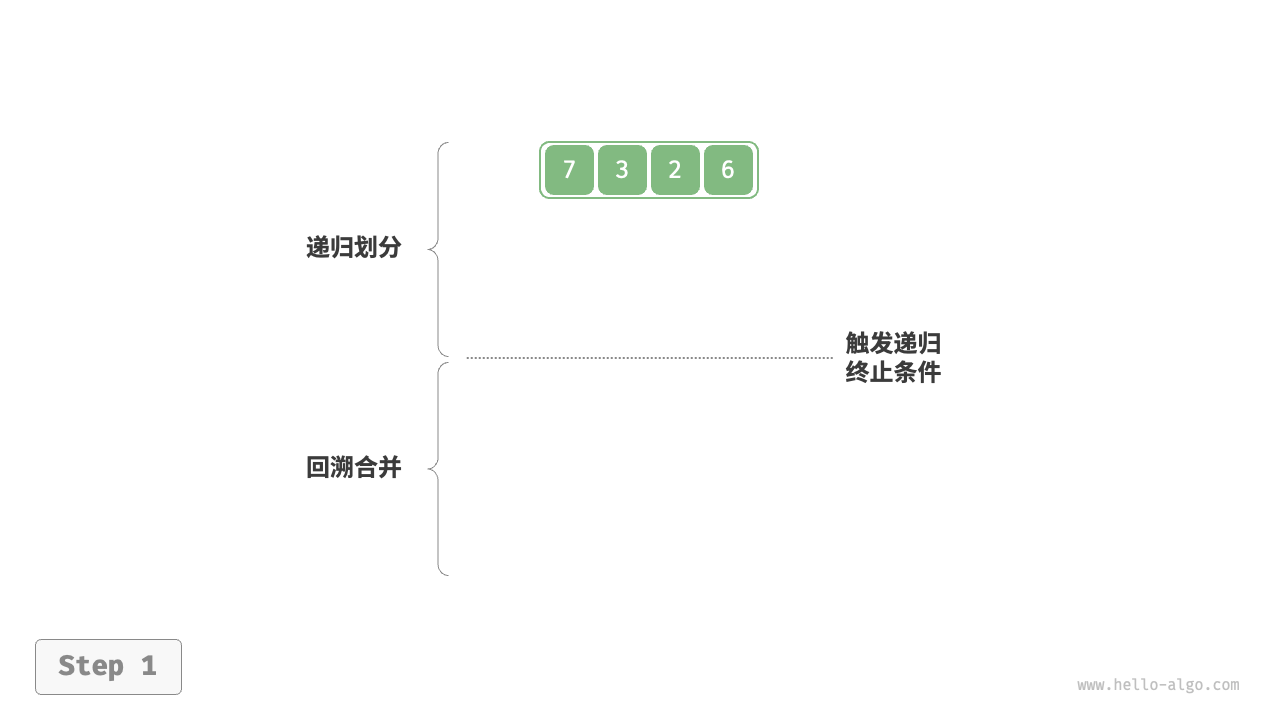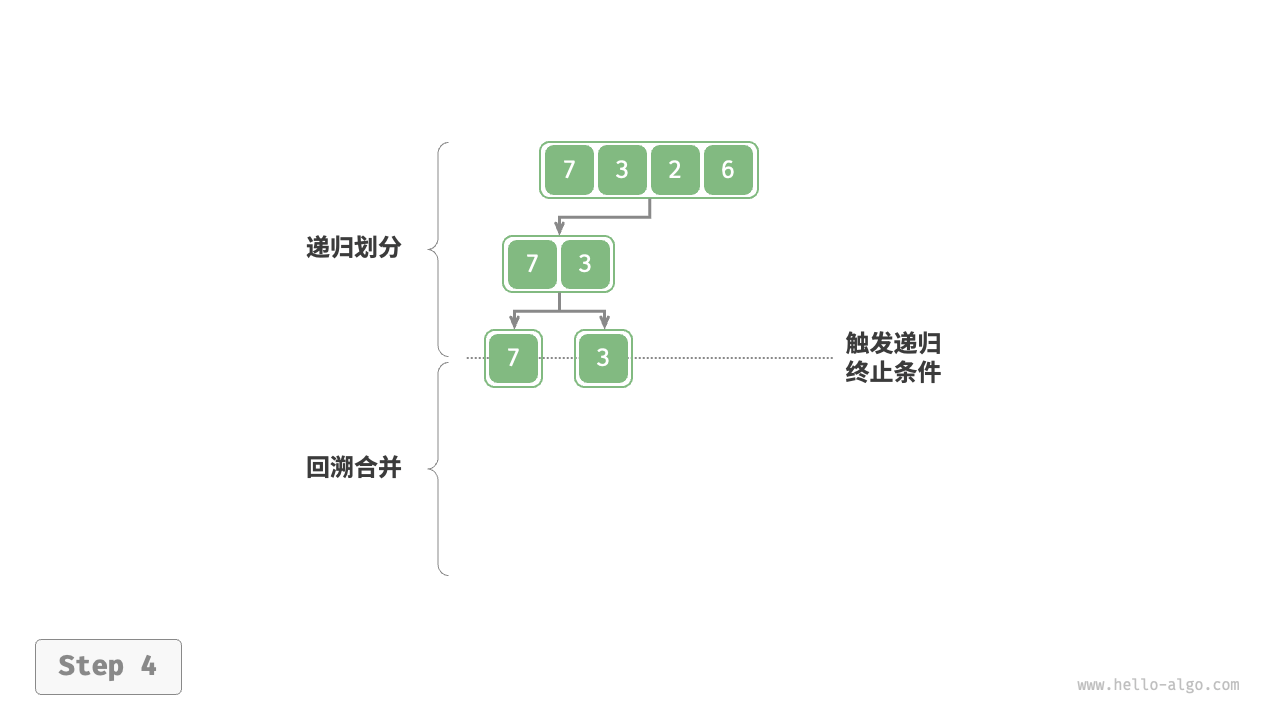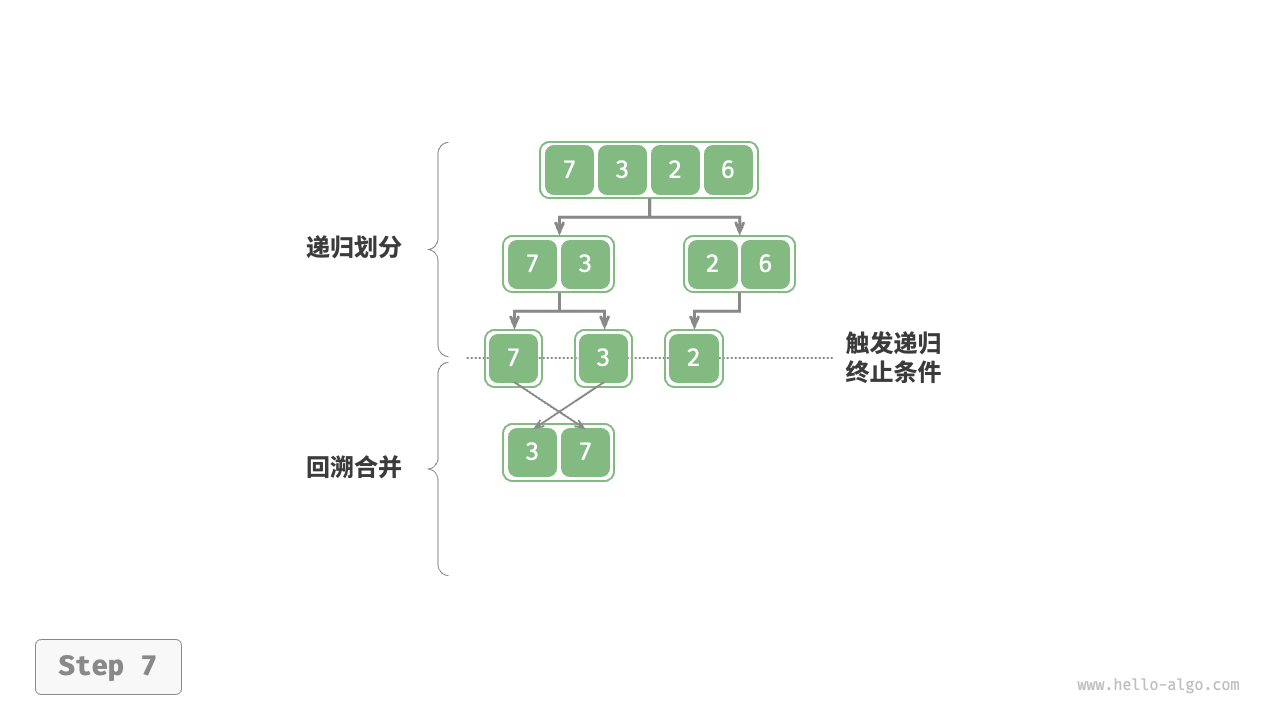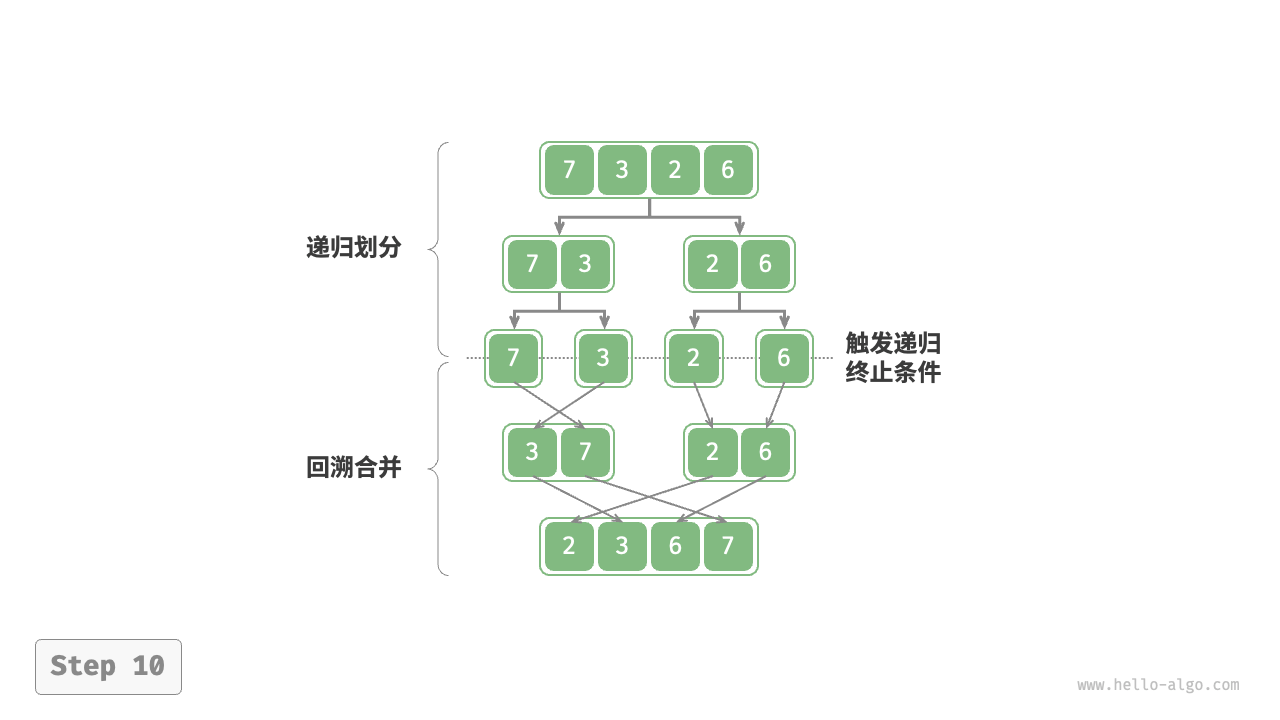
是一种基于分治策略的基础排序算法。

1.划分阶段：通过不断递归地将数组从中点处分开，将长数组的排序问题转化成段数组的排序问题。

2.合并阶段：当子数组的长度为1时终止划分，开始合并，持续不断地将左右两个较短的有序数组合并为一个较长的有序数组，直到结束。

##图例

##代码实现

1.向下递归，对半分割

2.递归返回条件：递归到最小，1个就是有序【控制的是范围，归并的是区间】

3.递归到最深处，最小时，就递归回去，开始分割按对半分割出的范围，将已有子序列合并，在tmp里面进行合并

4.再将tmp里形成的有序序列，拷贝回原数组【因下一次递归回去上一层的归并过程中，会将数据在tmp中进行归并，会将tmp中的数据覆盖，因此要及时，拷】

//python代码示例
def Merge(a, start, mid, end) :tmp = [] #创建一个临时列表，用来存储合并的值#两段起点的开始l = startr = mid + 1#当两段都没到达末尾，则继续循环，将其添加到tmpwhile l <= mid and r <= end :if a[l] <= a[r] :tmp.append(a[l])l += 1else :tmp.append(a[r])r += 1#此时肯定只剩下，单一的一个值，即将剩余元素塞入到tmp中tmp.extend(a[l:mid+1])tmp.extend(a[r:end+1])#将合并完成的元素，赋值到a原数组中for i in range(start,end+1):a[i] = tmp[i - start]print(start,end,tmp)def MergeSort(a,start,end) :#利用递归来实现归并排序，将大的问题分解成小的子问题if start == end : #当递归到数组只有一个元素时，直接返回returnmid = (start + end) // 2 #计算出mid，找到递归点MergeSort(a,start,mid) #左递归MergeSort(a,mid+1,end) #右递归Merge(a,start,mid,end)#左递归，左合并，右递归，右合并，类似于树的后序遍历a = [7,3,2,6]
MergeSort(a,0,3)

//c++代码实现示例
#include<iostream>
#include<vector>
using namespace std;
//c++代码实现示例
void merge(vector<int> &a, int left, int mid, int right)
{int i = left ;int j = mid + 1 ;int k = left ;vector<int> tmp(right - mid + 1) ;while ( i <= mid && j <= right ){if ( a[i] <= a[j] ){tmp[k++] = a[i++] ;}else{tmp[k++] = a[j++] ;}}while ( i <= mid ){tmp[k++] = a[i++] ;}while ( j <= right ){tmp[k++] = a[j++] ;}for (int m = left ; m <= right ; m++){a[m] = tmp[m - left] ;}cout << left << right << " " ;for (int n = 0 ; n < tmp.size() ; ++n){cout << tmp[n] << " " ;}
}void mergeSort(vector<int> &a, int left, int right)
{if (left >= right){return ;}int mid = (left + right) / 2 ;mergeSort(a,left,mid) ;mergeSort(a,mid+1,right) ;merge(a,left,mid,right) ;
}int main()
{
//	vector<int> arr = {1,2,3,4,5};
//	vector<int> arr;arr.push_back(7);arr.push_back(3);arr.push_back(2);arr.push_back(6);
//    arr.push_back(5);mergeSort(arr,0,3) ;return 0 ;}

void _MergerSort(DataType* a ,DataType* tmp, int begin,int end)
{//递归返回条件，不正常的范围，或只剩下一个数 if (begin >= end){return ;}int mid = (begin + end) / 2 ;//递归过程 _MergeSort(a,tmp,begin,mid) ;_MergeSort(a,tmp,mid+1,end) ;//合并过程 //归并到tmp数组中，再拷贝回去 int begin1 = begin ;int end1 = mid ;int begin2 = mid + 1 ;int end2 = end ;//指向tmp,=begin是 根据要进行比较插入的数组的位置 找到其对应在tmp中所对应的位置，则不会覆盖前面已经排好序的数据int index = begin ;while (begin1 <= end1 && begin2 <= end2){if (a[begin1] < a[begin2]){tmp[index++] = a[begin++] ;}else{tmp[index++] = a[begin2++] ;}}//剩下还没有插入进去的 while (begin1 <= end1){tmp[index++] = a[begin1++];}while (begin2 <= end2){tmp[index++] = a[begin2++] ;}//拷贝回去原数组a中memcpy(a+begin,tmp+begin,sizeof(DataType)*(end-begin+1)) ; 
}void MergeSort(DataType* a, int n)
{DataType* tmp = (DataType*)malloc(sizeof(DataType)*n) ;if (tmp == NULL){perror("malloc fail") ;return ;}_MergeSort(a,tmp,0,n-1) ;free(tmp) ;
}

对于链表，归并排序相较于其他排序算法具有显著优势，可以将链表排序任务的空间复杂度优化至 𝑂(1) 。

• 划分阶段：可以使用“迭代”替代“递归”来实现链表划分工作，从而省去递归使用的栈帧空间。
• 合并阶段：在链表中，节点增删操作仅需改变引用（指针）即可实现，因此合并阶段（将两个短有序链表合并为一个长有序链表）无须创建额外链表。

##非递归实现归并排序

##释

归并排序时二分的思想=>logN层=>递归不会太深、且现在编译器优化后，递归、非递归的性能差距没有特别大了=>所以可以不用考虑非递归。

递归的缺点：递归消耗栈帧，递归的层数太深，容易爆栈。

【栈的空间比较小，在x86(32位)环境下，只有8M。（对比同一环境下的堆，则有2G+）。因为平时函数调用开不了多少个栈帧。理论上递归深度>1w 可能就会爆 ，但实际上5k左右就爆掉了】，这时就需要改非递归了。

非递归改写方法：

1.改变循环

2.利用数据结构栈（本质是通过malloc在堆上开辟的存储空间，内存空间需要足够大）

3.递归逆着求-实际上也差不多也是递归思想（如斐波那契数列逆着来求也是可行的）

#代码实现

1. 开辟新的数组（临时存放）用于归并排序过程
2. int gap=1；gap*=2【gap控制归并的范围：11归并，22归并，44归并】
3. for (int i = 0; i < n; i += 2 * gap) { 【i 控制进行比较轮到的组号，控制进行归并的组号】
4. 归并完一轮，将归并好的有序数组拷贝回原数组memcpy 。
5. 进入新的一轮归并，直至gap>n则归并完成

     ☆注意的两个情况

     6. if (begin2 >= n) { break; } 第二组不存在，这一组不用归并了 

     7. if (end2 > n) { end2 = n - 1; } 第二组右边界越界问题，修正一下

void MergerSortNonR(DataType* a, int n)
{DataType* tmp = (DataType*)malloc(sizeof(DataType) * n);   //开辟新的数组（临时存放）用于归并排序过程if (tmp == NULL){perror("malloc fail") ;return ;}int gap = 1 ;while (gap < n) {for (int i = 0 ; i < n ; i += 2 * gap){
//            // 1 , 1 归并 
//            // 2 , 2 归并
//            //4 , 4 归并 
//            //[begin1,end1][begin2,end2]归并 int begin1 = i ;int end1 = i + gap - 1 ;int begin2 = i + gap ;int end2 = i + 2 * gap - 1 ;//            //如果第二组不存在，这一组不用归并了if (begin2 >= n) {break;}//第二组右边界越界问题，修正一下if (end2 > n) {end2 = n - 1;}
//            
//            //当beigin2 超过 n 的时候，直接break掉就OK了
//            //但end2 超过 n 的时候，需要修改边界问题 n - 1 
//            int index = i ;while (begin1 <= end1 && begin2 <= end2){if (a[begin1] < a[begin2]){tmp[index++] = a[begin1++] ;}else{tmp[index++] = a[begin2++] ;}}while (begin1 <= end1){tmp[index++] = a[begin1++] ;}while (begin2 <= end2){tmp[index++] = a[begin2++];}
//            //为什么这里不能是，2 * gap呢，不一定是2*gap的数都拷贝过去，memcpy(a+i,tmp+i,sizeof(DataType)*(end2 - beigin1 + 1)) 错误 
//            // memcpy(a+i,tmp+i,sizeof(DataType)*(end2 - begin1 + 1)) ; 因为begin1++会发生改变的，因此不可以，错误 memcpy(a+i,tmp+i,sizeof(DataType)*(end2 - i + 1)) ;
//            
//        }printf("\n");
//        for (int k = 0 ; tmp.size() ; k ++)
//        {
//            printf("%d",tmp[k]) ;
//        }gap = gap * 2 ;}free(tmp);
}
}

def MergeSort(a, n) :tmp = [0] * (n+1)gap = 1while (gap < n) :z = gap * 2for i in range(0,n,z) :begin1 = iend1 = i + gap - 1begin2 = i + gapend2 = i + 2 * gap - 1if begin2 > n :breakif end2 > n :end2 = n - 1index = iwhile begin1 <= end1 and begin2 <= end2 :if a[begin1] < a[begin2] :tmp[index] = a[begin1]index += 1begin1 += 1else :tmp[index] = a[begin2]index += 1begin2 += 1while begin1 <= end1 :tmp[index] = a[begin1]index += 1begin1 += 1while begin2 <= end2 :tmp[index] = a[begin2]index += 1begin2 += 1for j in range(i,end2 + 1) :a[j] = tmp[j - i]print()# print(tmp)gap = gap * 2

这篇关于算法学习笔记（5.0）-基于比较的高效排序算法-归并排序的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---