代码随想录算法训练营第二十九天 | 39. 组合总和、40.组合总和II、131.分割回文串

本文主要是介绍代码随想录算法训练营第二十九天 | 39. 组合总和、40.组合总和II、131.分割回文串，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

39. 组合总和

题目链接/文章讲解：代码随想录

视频讲解：带你学透回溯算法-组合总和（对应「leetcode」力扣题目：39.组合总和）| 回溯法精讲！_哔哩哔哩_bilibili

解题思路

这里和组合不同的是元素可以重复选取，其实也就是注意startindex的位置就可以，深度控制是由k的值来进行的

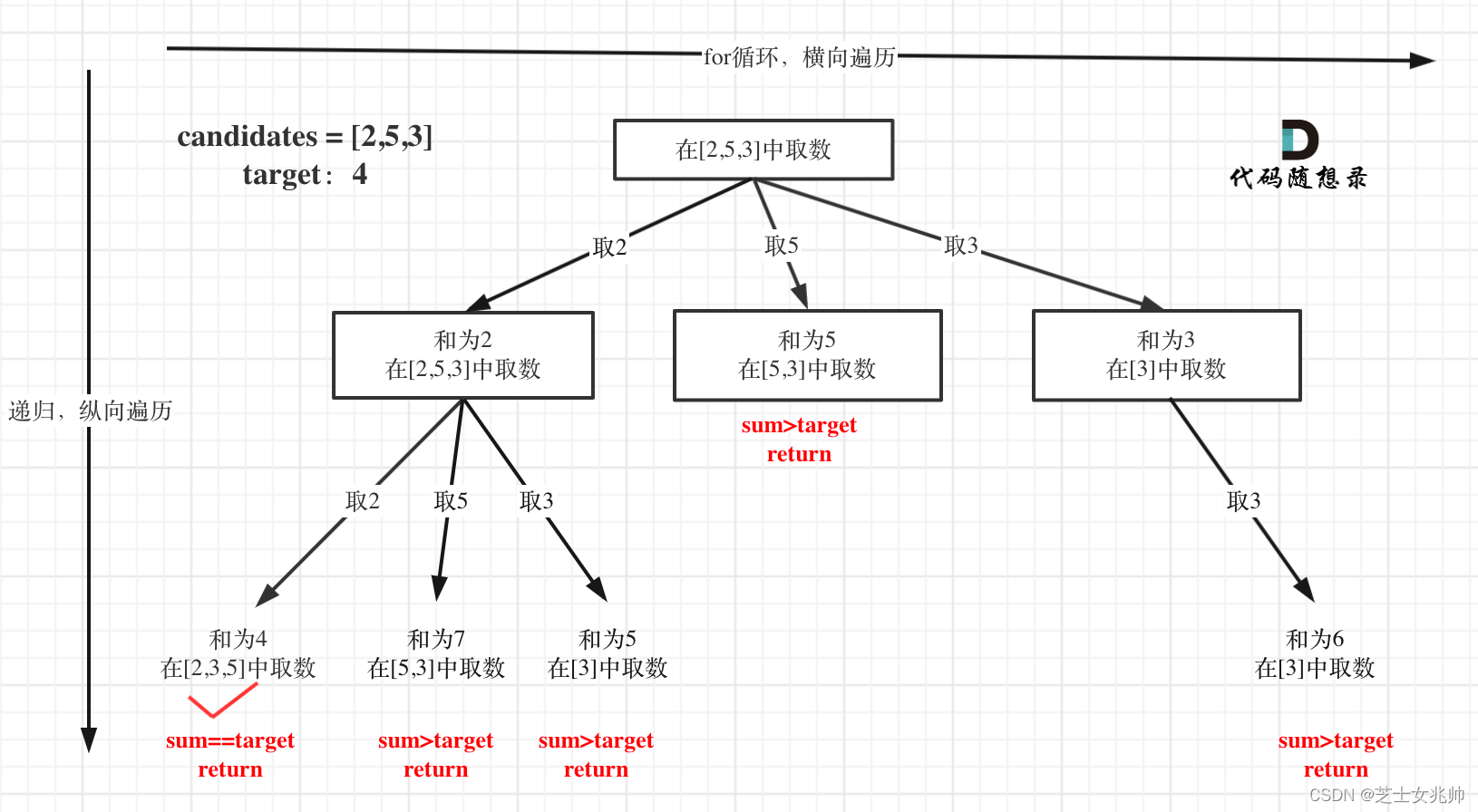
剪枝操作

剪枝一般都是在for循环上做操作，因为多了一些分支

而这题，我们只需要将数组排序后，例如235，和为4，当2+3已经大于4了，就没必要去遍历5了，因此在for循环中多加个判断条件即可

class Solution {
private:
vector<int> path;
vector<vector<int>> result;
int sum =0;public:void backtracking(vector<int>& candidates, int sum , int target , int startIndex){if(sum == target){result.push_back(path);return;}for(int i = startIndex ; i<candidates.size()&& sum + candidates[i] <=target;i++)   //将数组排序后，如果这个数和另一个数相加已经大于taget了，那么后面的数也就没有必要继续遍历了{sum+=candidates[i];path.push_back(candidates[i]);backtracking(candidates,sum,target,i);path.pop_back();sum-=candidates[i];}}vector<vector<int>> combinationSum(vector<int>& candidates, int target) {//对数组进行排序，方便后面的剪枝操作sort(candidates.begin(),candidates.end());backtracking(candidates,sum,target,0);return result;}
};

40.组合总和II

题目链接/文章讲解：代码随想录

视频讲解：回溯算法中的去重，树层去重树枝去重，你弄清楚了没？| LeetCode:40.组合总和II_哔哩哔哩_bilibili

解题思路

这道题中是有重复元素的，去重我们考虑，树枝去重（深）和树层去重（宽）

这题的去重逻辑，其实和三数之和很像，我们排完序后，在树枝上，我们取重复元素是可以的，但是在树层，在遇到相同的，也就是已经走过的路了，那就不要再走了，直接剪枝就可以了，但是我们如何去判断这是在树层上，还是在树枝上？我们只需要用uesd数组，当i-1的位置为0，说明在树层上，i-1的位置为1，说明在树枝上。

后面基本回溯的去重写法都是这个！！！非常重要

class Solution {
private:
vector<vector<int>> result;
vector<int> path;
public:void backtracking(vector<int>& candidates, int target, int sum , int startIndex , vector<int>& used){if(sum == target){result.push_back(path);return;}for(int i= startIndex; i<candidates.size() && sum + candidates[i] <= target; i++){if(i>0 &&candidates[i]== candidates[i-1] && used[i-1]==0) continue;   //如果前一个used为1的话，表明在树枝上path.push_back(candidates[i]);sum += candidates[i];used[i] = 1 ;backtracking(candidates,target,sum, i+1,used);used[i] = 0 ;sum -= candidates[i];path.pop_back();}}vector<vector<int>> combinationSum2(vector<int>& candidates, int target) {vector<int> used(candidates.size(),0);sort(candidates.begin(),candidates.end());backtracking(candidates,target,0,0 , used);return result;}
};

131.分割回文串

代码随想录

视频讲解：带你学透回溯算法-分割回文串（对应力扣题目：131.分割回文串）| 回溯法精讲！_哔哩哔哩_bilibili

解题思路

本题主要要理解的是如何画树形结构

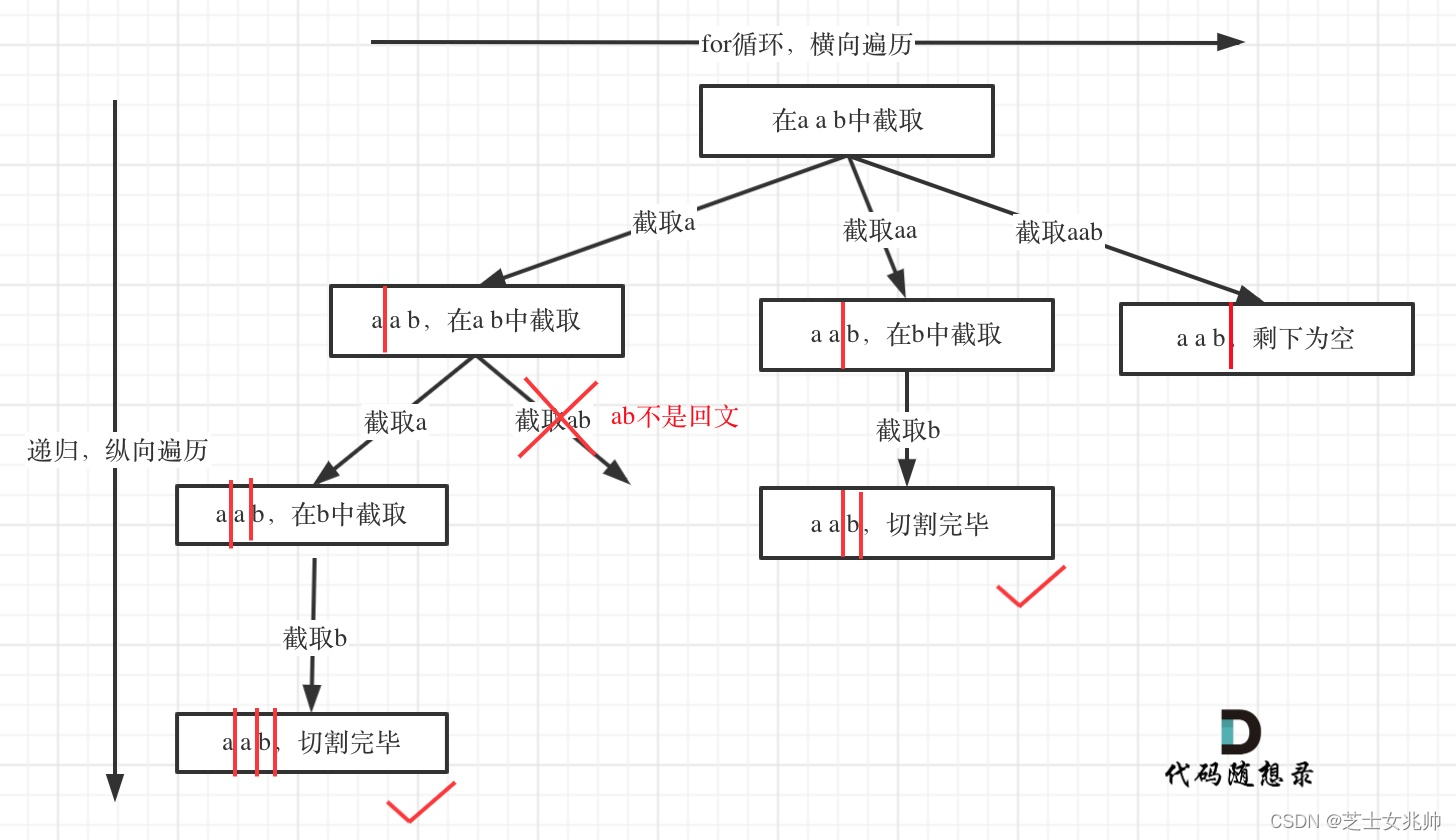其本质和组合问题是一样的，从图上说明更明确

这里我们进行切割的话，是使用startIndex来进行标记的，而在横向的切割中，是用i去寻找下一个切割点的，因此我们截取字符串也是从[stratIndex,i]去截取的

class Solution {
private:
vector<string> path;
vector<vector<string>> result;bool isHuiWenStr(const string& s, int a, int b){//利用双指针来判断回文串for(int i=a,j=b;i<=j;i++,j--){if(s[i]!=s[j])return false;}return true;}void backtracking(const string& s, int startIndex)  //这里是用startIndex来分割字符串的，本质和组合问题是一样的{//终止条件，因为是用startindex来分割的，那么当startindex的位置已经位于字符串最后说明分割完了if(startIndex >= s.size()){result.push_back(path);return;}//单层处理逻辑for(int i= startIndex; i< s.size();i++){if(isHuiWenStr(s,startIndex,i)){string str = s.substr(startIndex,i-startIndex+1);    //截取字符串函数，变量分别为索引和个数path.push_back(str);}elsecontinue;backtracking(s,i+1);path.pop_back();}}
public:vector<vector<string>> partition(string s) {backtracking(s,0);return result;}
};