分享几道适合用来面试的 LeetCode 算法题

Hi，大家好，这几天公司忙着年会，整个大部门去西安出差了几天，今天刚刚回来，所以我这几天没有怎么搭理公号。

年会那会也忙不少事情，由于今年是我刚刚入职，所以还要表演节目，排练了一个舞蹈《红昭愿》上台表演，为此也花了不少心思，另外其他时间就是参加年度总结大会，整个时间安排还是比较紧的。

不过这期间抽空也做了点东西，最近几天我一个在忙着搭建 NightTeam 的官网和博客，另外又整理了一下爬虫第二版的书稿，出于安全考虑再删减和修改一些敏感内容。本想今天把前者写一篇记录发出来的，但感觉今天时间不太够了，明天再发吧。

另外想到前一阵子还和好朋友合作了一个公号，叫做「CodeWeekly」，目标就是在于分享一些 LeetCode 或周赛题解，提供一些题目的解析。这位朋友是一位 ACM 大神，获得过多个 ACM 国际比赛的奖牌了，这个号也主要由他来打理，质量还是很有保证的。正好上周 LeetCode 周赛的题目质量还是比较高的，上周日他在号里面分享了一下题解，我看完之后确实收获也挺大的，感觉确实可以好好研读一下，甚至把这几道题目作为面试题来对待了。

所以这篇文章就转来分享一下上周 LeetCode 周赛的几道比较不错的算法题，并附上详细的解析，大家有兴趣可以看看。

题目在 LeetCode 官方网站上面，周赛链接是：https://leetcode.com/contest/weekly-contest-155，大家可以先去了解一下，然后再回来看看解析会更好。

下面就是题解了，希望对大家有帮助。

比赛总结：本期周赛题目质量较高，更多侧重于对思维和常见算法的理解和考察，总体考察的知识点很多，但是代码量除了最后一题以外并不大，适合用作面试题目。

Easy 5197. 最小绝对差

题目

给你个整数数组 arr，其中每个元素都不相同。

请你找到所有具有最小绝对差的元素对，并且按升序的顺序返回。

示例 1：

---

示例 2：

---

示例 3：

题目解析

O(n^2log(n))解法

拿到题目(特别是面试的时候)，我们首先需要保证自己能给出来一个可行解。那么对于这道题目，我们可以按照下列思路来得到一个结果：

1. 枚举所有的二元组<i,j>，计算arr[i]和arr[j]的差，记录其中的最小值。

2. 枚举所有的二元组<i,j>，计算arr[i]和arr[j]的差，将差值等于最小值的二元组记录。

3. 将所有二元组按升序排序。

前两步需要遍历所有的二元组，所以计算复杂度为: O(n^2),而第三步我们还需要对二元组排序，所以时间复杂度为O(n^2log(n))。

O(nlog(n))解法

那么，至少我们现在有一个O(n^2log(n))的算法了，我们来思考一下有没有什么优化空间。题目要求最小的绝对差，那么如果要差最小的话，两个做差的数一定会是序列排序后相邻的两个数。

基于这个结论，我们可以将整个数组排序，然后计算所有相邻的数的差，再仿照上面的思路求得所有的元素对，现在的思路是：

1. 排序数组，枚举所有相邻的二元组<i,i+1>，计算arr[i]和arr[i+1]的差，记录其中的最小值。

2. 枚举所有的二元组<i,i+1>，计算arr[i]和arr[i+1]的差，将差值等于最小值的二元组记录。

3. 将所有二元组按升序排序。

由于我们现在只计算相邻元素的差，所以枚举的时间复杂度从O(n^2)降为了O(n)，总体时间复杂度为O(nlog(n))。下面为实现代码。

class Solution(object):def minimumAbsDifference(self, arr):""":type arr: List[int]:rtype: List[List[int]]"""arr = sorted(arr)mindiff = min([arr[i]-arr[i-1] for i in range(1,len(arr))])arr = [[arr[i-1],arr[i]] for i in range(1,len(arr)) if mindiff == arr[i]-arr[i-1]]return arr

Medium 5198. 丑数 III

题目

请你帮忙设计一个程序，用来找出第 n 个丑数。

丑数是可以被 a 或 b 或 c 整除的正整数。

示例 1：

---

示例 2：

题目解析

题目本身来说并不算太难，但是有不少同学被丑数本身的定义绕进去了。这也是算法题目题面中很容易发生的事情，那就是题目所给的定义不一定就是其原有定义。例如我们回到这道题，丑数的定义为能被所给abc任一整除的正整数，显然是和之前丑数相关题目是不一样的。在这种时候，我们需要跳开之前的固有思维，来重新考虑在所给条件下，如何求当前的"丑数"。

暴力解法

我们同样有一个可以暴力解决问题的办法，那就是我们从1开始枚举，然后看看这个数能不能被abc其中某个数整除来判断其是不是丑数，最后到第n个丑数就是我们的答案了。这样做的话时间复杂度为O(n),由于n给的10^9，超过了我们说的10^8的限制，所以显然会超时(当然这和面试能拿到一些分数并不冲突，所以并不是完全没有意义)。

O(log(n))解法

原始问题有a,b,c三个因子，我们可以先试图简化问题来寻找灵感。

1. 假设我们现在只有一个a: 例如a等于2，那么丑数序列就是2,4,6,8…，那么这时如果给了一个数n，那么我们知道[1,n]中一共有Floor(n/2)个丑数，其中Floor是向下取整。如果n也是丑数，那么n一定是第Floor(n/2)个丑数。

2. 假设我们现在有a和b: 例如a等于2，b等于3，那么丑数序列是2,3,4,6,8,9…，这时再给一个整数n，[1,n]中又有多少丑数呢？[1,n]，他能被2整除的数有Floor(n/2)个，这些数肯定是丑数没错了，他能被3整除的数有Floor(n/3)个，这些数也是丑数。但是我们别忘了，还有一些数是能同时被2和3整除的，也就是能被6整除，这些数我们计算了两次。那么减掉这些重复的数以后，剩余的丑数还剩下Floor(n/2)+Floor(n/3)-Floor(n/6)个。那么我们知道，在[1,n]区间内有这么多丑数。

我们现在可以回到原问题的三个数了，这就是一个典型的容斥原理了，如下图，对于3个数的情况，对应的丑数数量为Floor(n/a)+Floor(n/b)+Floor(n/c)-Floor(n/lcm(a,b))-Floor(n/lcm(b,c))-Floor(n/lcm(a,c))+Floor(n/lcm(a,b,c))，其中lcm是最小公倍数。通过这个公式，我们可以方便的求出[1,n]中的丑数数量。

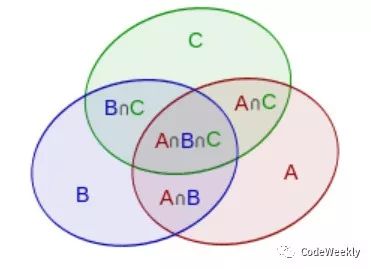
但是这离我们解决问题还有一段距离，我们现在想知道的是第n个丑数是什么，而不是[1,n]中有多少丑数。我们来思考一下对于第n个丑数Un来说，他会满足什么性质：

1. 显然[1,Un]中有n个丑数。

2. [1,Un-1]中有n-1个丑数。

那么由于随着数的变大，丑数的数量肯定是单调递增的，那么我们可以利用二分查找来逐步逼近某个临界点，满足[1,Un]有n个丑数且[1,Un-1]中有n-1个丑数。这样时间复杂度仅为二分查找的时间复杂度O(log(n))。O(log(n))级别的实现方法的，文末也会给出相关资料【1】。

from fractions import gcd
class Solution(object):def nthUglyNumber(self, n, a, b, c):""":type n: int:type a: int:type b: int:type c: int:rtype: int"""//最小公倍数def lcm(a,b):return a*b/gcd(a,b)//计算[1,mid]有多少丑数//这种实现时间复杂度会高一个log(n)数量级，最小公倍数可以预处理。def get_idx(mid):return mid // a + mid // b + mid // c - mid //lcm(a,b) - mid//lcm(b,c) - mid //lcm(c,a) + mid//lcm(lcm(a,b),c)l = 1; r = 2*10**9+1while ( l < r ):mid = (l+r+1)/2idx = get_idx(mid)if idx == n:l = midbreakelif idx < n:l = midelif idx > n:r = mid-1//这里的实现略微有些不一样，可以思考一下现在的做法return l-min(l%a,min(l%b,l%c))

Medium 5199. 交换字符串中的元素

题目

给你一个字符串s，以及该字符串中的一些「索引对」数组 pairs，其中pairs[i] = [a, b]表示字符串中的两个索引（编号从0开始）。

你可以任意多次交换在pairs中任意一对索引处的字符。

返回在经过若干次交换后，s 可以变成的按字典序最小的字符串。

示例 1:

---

示例 2：

题目解析

这道题理论上我们也是可以暴力的：搜索所有的交换然后同时保留我们的中间状态，记录全部状态的字典序最小值，但是这样的话是一个指数级别复杂度的算法了。

考虑一个字符串s，如果他的位置a和b能交换，且b和c能交换，那么由于我们的交换没有限制，我们可以把abc三个位置排成任意我们想要的排列。

这里我们可以简单证明一下，对于a和b能交换的情况，我们可以得到[a,b]和[b,a]两种排列，即2个数的时候我们可以得到任意排列。

那么三个数的时候，例如[a,b,c]，由于2个数的时候我们可以得到任意排列，那么我们最后把c不停地向前交换，可以把c放在任意位置，也即是3个数我们也可以得到任意排列。我们还可以继续推广一下，如果有[a,b],[b,c][c,d],[d,e]...，对于[a,b,c,d,e...]位置的字母，我们可以得到其任意排列。

这个结论就很有作用了，令place={a,b,c,d,e...}，由于我们需要原始字符串最小，那么对于place位置的字母，肯定是将其重排为字典序最小字符串，如下图，假设红色部分为一个place集合。

那么原问题就可以分为两步：

1. 得到每个点所属的place集合

2. 将所有place集合中的字符重排为字典序最小排列。

先来解决第一个问题，我们要知道哪些点属于同一个place集合，那么对于所有给的边[a,b]，我们知道[a,b]是属于一个集合的，如果集合还有边连向外面例如[a,c]，我们知道c也属于这个集合。这种问题特性我们可以使用并查集来进行维护，最后得到每个点所属的集合id。对于不了解并查集的同学，这里也整理了一些资料【2】。

并查集时间复杂度为O(n)，排序时间复杂度为O(log(n))，所以总体时间复杂度为O(nlog(n))，当然，由于这里是字符串排序，我们可以使用桶排序来将时间复杂度优化为O(n)。

下面是实现代码

import numpy as np
class Solution(object):def smallestStringWithSwaps(self, s, pairs):""":type s: str:type pairs: List[List[int]]:rtype: str"""#并查集的find函数def ffind(a):if a == fa[a]:return af = ffind(fa[a])fa[a] = freturn f#并查集的union函数def union(a,b):a = ffind(a)b = ffind(b)fa[a] = b#并查集维护集合n = len(s)fa = np.arange(n)for a,b in pairs:union(a,b)for i in range(n):ffind(i)#得到所有place集合unique_fa = np.unique(fa)#得到所有place集合中对应的字符串并排序fa_str = {x:'' for x in unique_fa}for i in range(n):fa_str[fa[i]] += s[i]for x in unique_fa:fa_str[x] = sorted(fa_str[x])fa_cnt = {x:0 for x in unique_fa}#将排序完的字符串反映射回原串得到最后结果ans = ''for i in range(n):x = fa[i]ans += fa_str[x][fa_cnt[x]]fa_cnt[x] += 1return ans

Hard 5200. 项目管理

提示：该题实际难度略小于hard，可以尝试

题目

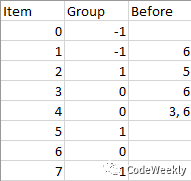
公司共有 n 个项目和 m 个小组，每个项目要不没有归属，要不就由其中的一个小组负责。

我们用 group[i] 代表第 i 个项目所属的小组，如果这个项目目前无人接手，那么 group[i] 就等于 -1。（项目和小组都是从零开始编号的）

请你帮忙按要求安排这些项目的进度，并返回排序后的项目列表：

同一小组的项目，排序后在列表中彼此相邻。beforeItems 来表示，其中 beforeItems[i] 表示在进行第 i 个项目前（位于第 i 个项目左侧）应该完成的所有项目。

如果存在多个解决方案，只需要返回其中任意一个即可。

如果没有合适的解决方案，就请返回一个空列表。

示例 1：

---

示例 2：

题目解析

这道题是一道拓扑排序的变种，本身虽然比较复杂但是理清楚了并不是特别难，之所以被排到hard可能是因为题目实在是太难懂了~ ~。

1. 有很多任务，任务分成了若干个组，一个组的任务必须要连续做完，不能先做组a的任务，然后去做组b的，然后又跑来做组a的。

2. 任务之间有一些依赖关系，对于每个任务给了其依赖任务，需要所有依赖任务完成后才能开始该任务，例如1:[2,6]，那么任务1需要在任务2和任务6都完成以后才能开始。

3. 最后，我们还是要一个合法的任务序列，保证依赖关系不冲突，且组内的任务是连着做的。

那么根据这些条件，一个可能的依赖情况是这样的：

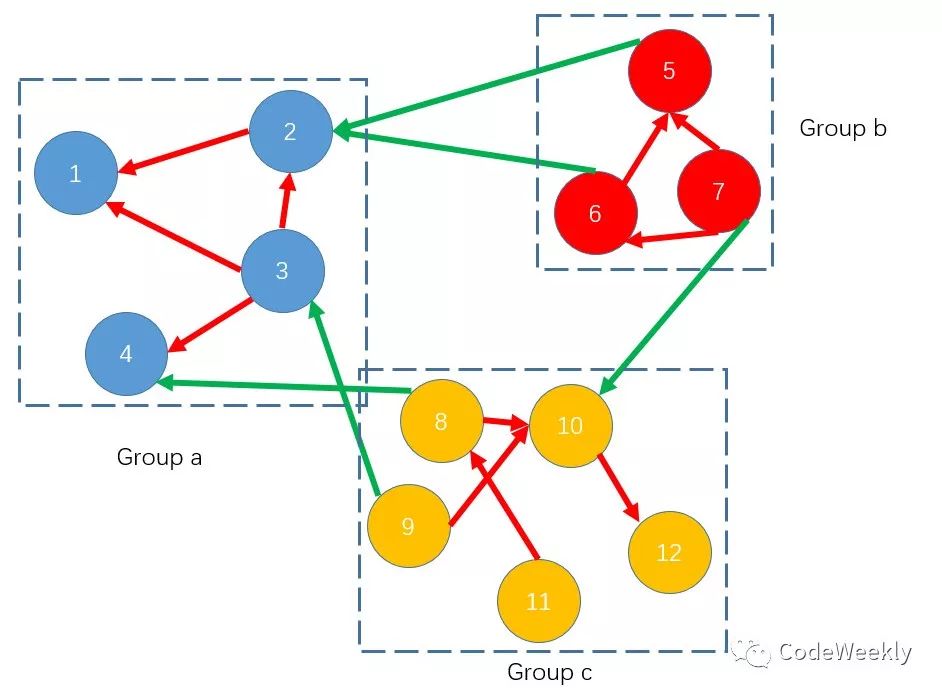
我们看到，依赖关系实际上分为两种，一种是组内依赖关系(红色箭头)，一种是组间依赖关系(绿色箭头)。由于一个组的任务需要连着做，我们先不考虑组内依赖关系，那么从组的角度来看：

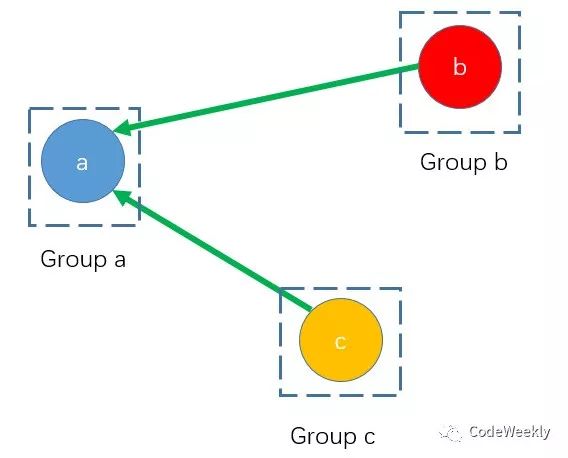
这就是一个典型的拓扑排序问题了！我们可以很容易的求出可行的调度序列，当然这个序列是组级别的，也即是我们先执行哪个组的任务，再执行哪个组的任务的序列。

那么组的执行顺序知道了，接下来我们只需要看每个组内的任务该如何执行就可以了。如下图，对于一个组内的任务，我们发现他还是一个朴素的拓扑排序问题：

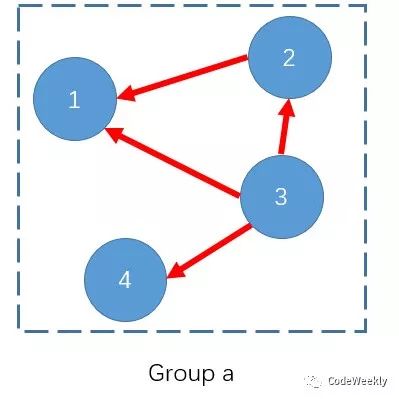
那么接下里的思路也有了，我们对于每个组内的任务再分别建图求拓扑序，最后根据组级别的拓扑序将结果整合起来就可以了。当然，如果任一个拓扑排序发现无可行解，那么整个系统就无可行解。

总体时间复杂度为O(N)，以下为实现代码：

import Queue
import numpy as np
class Solution(object):def sortItems(self, n, m, group, beforeItems):""":type n: int:type m: int:type group: List[int]:type beforeItems: List[List[int]]:rtype: List[int]"""#组内拓扑排序def get_group_ans(group_points,group_edges):#组内级别建图graph = {group_point:[] for group_point in group_points}degree = {group_point:0 for group_point in group_points}for x,y in group_edges:graph[y].append(x)degree[x] += 1#top sortq = Queue.Queue()for graph_point in group_points:if degree[graph_point] == 0:q.put(graph_point)#组内拓扑排序task_res = []while not q.empty():x = q.get()task_res.append(x)for y in graph[x]:degree[y] -= 1if degree[y] == 0:q.put(y)if len(task_res) != len(group_points):return Nonereturn task_resgroup_cnt = max(group)+1for i in range(n):if group[i] == -1:group[i] = group_cntgroup_cnt += 1#组级别建图group_ids = np.unique(group)graph = {group_id:[] for group_id in group_ids}degree = {group_id:0 for group_id in group_ids}group_inner_edges = {group_id:[] for group_id in group_ids}group_points = {group_id:[] for group_id in group_ids}for i in range(n):groupa = group[i]group_points[groupa].append(i)for j in beforeItems[i]:groupb = group[j]if groupa == groupb:group_inner_edges[groupa].append([i,j])continuegraph[groupb].append(groupa)degree[groupa] += 1#组级别拓扑排序q = Queue.Queue()for group_id in group_ids:if degree[group_id] == 0:q.put(group_id)group_res = []while not q.empty():x = q.get()group_res.append(x)for y in graph[x]:degree[y] -= 1if degree[y] == 0:q.put(y)if len(group_res) != len(group_ids):return []#根据组拓扑序整合结果task_res = []for group_id in group_res:ans = get_group_ans(group_points[group_id],group_inner_edges[group_id])if ans is None:return []task_res += ansreturn task_res

参考资料：

[1] 辗转相除法求最大公约数

最后大家如果想了解更多优质 LeetCode 题解和周赛解析的话，可以关注一下「CodeWeekly」这个公号，希望对大家有帮助，谢谢。

崔庆才

静觅博客博主，《Python3网络爬虫开发实战》作者

隐形字

个人公众号：进击的Coder

长按识别二维码关注