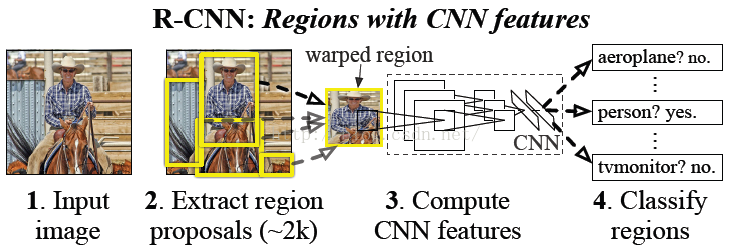
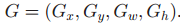本文主要是介绍RCNN系列(注意事项及简单步骤),希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
原文地址:https://blog.csdn.net/poorfriend/article/details/51604385
训练过程:
step 1: 对于每张图片,利用选择性搜索(SS,Selective Search)找出2K个候选区域。对每个候选区域改变其尺度和长宽比,使其与卷积神经网络要求的图片输入的规格保持一致。
step 2: 利用Alexnet或VGGnet初始化CNN,将最后的1000类分类器替换成21类(20类+背景)分类器,随机初始化这层权重,然后就是整个网络的fine-tuning。训练时候选区域中,与GT box(grand-true box)的IOU大于0.5标为正样本,其余为负样本。从正样本中随机抽取32个,负样本中随机抽取96个,构成一个128的min-batch。
step 3: 利用步骤2调整好的网络(前面的网络已经是固定了)提取特征,用SVM分类。GT box标为正,其他候选区域中与GT box的IOU小于0.3标为负,其他的舍去。step 4: 边框回归
注:
1 改变图片大小,文中给出了几种方法:
(1)各向异性缩放, 我的理解是长宽放缩不同的倍数:
这种方法很简单,就是不管图片的长宽比例,管它是否扭曲,进行缩放就是了,全部缩放到CNN输入的大227*227,如下图(D)所示;
(2)各向同性缩放,长宽放缩相同的倍数
A、“tightest square with context”:把region proposal的边界进行扩展延伸成正方形,灰色部分用原始图片中的相应像素填补,如下图(B)所示;
B、“tightest square without context”:把region proposal的边界进行扩展延伸成正方形,灰色部分不填补,如下图(C)所示;
在放缩之前,作者也考虑了,在region proposal周围补额外的原始图片像素(pad p)。两张图片第一层p=0,第二层p=16.
2 正负样本和softmax的问题:
为什么最后分类的时候用SVM代替了softmax,因为作者通过实验发现还是SVM更好。那为什么不一开始就用SVM做fine-tuning呢?我认为是SVM是一个二分类器,并不适合做fine-tuning。当用softmax做fine-tuning时,如果采用和SVM一样的区分正负样本策略,则效果会差很多。作者猜测是因为这样做会引起样本数太少导致过拟合。softmax区分样本的方法更宽泛,将正样本的数量提高近30倍,这样就避免了过拟合。值得注意的是,这样做得到的结果是次优的,因为并没有用精确的定位以及更严格的负样本来fine-tuning。svm训练的时候,因为svm适用于少样本训练,所以对于训练样本数据的IOU要求比较严格。
3 边框回归:
用SVM为每个region proposal评分后,可以用边框回归找到更精确地定位。这些边框回归器是按类来训练的。
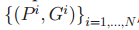
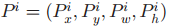
P和G分布候选区域和GT Box,P和G的IOU必须达到某个阈值(文中是0.6)。下面不加说明的话省略上标i.。公式中x,y代表区域中心坐标,w,h代表长和高。是region proposal经变换后的新区域。
据作者的结论,对候选区域评分和边框回归只进行一次,多次迭代,并无提升。
这篇关于RCNN系列(注意事项及简单步骤)的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!