【中级软件设计师】上午题16-算法（应试考试简略版）

本文主要是介绍【中级软件设计师】上午题16-算法（应试考试简略版），希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

---

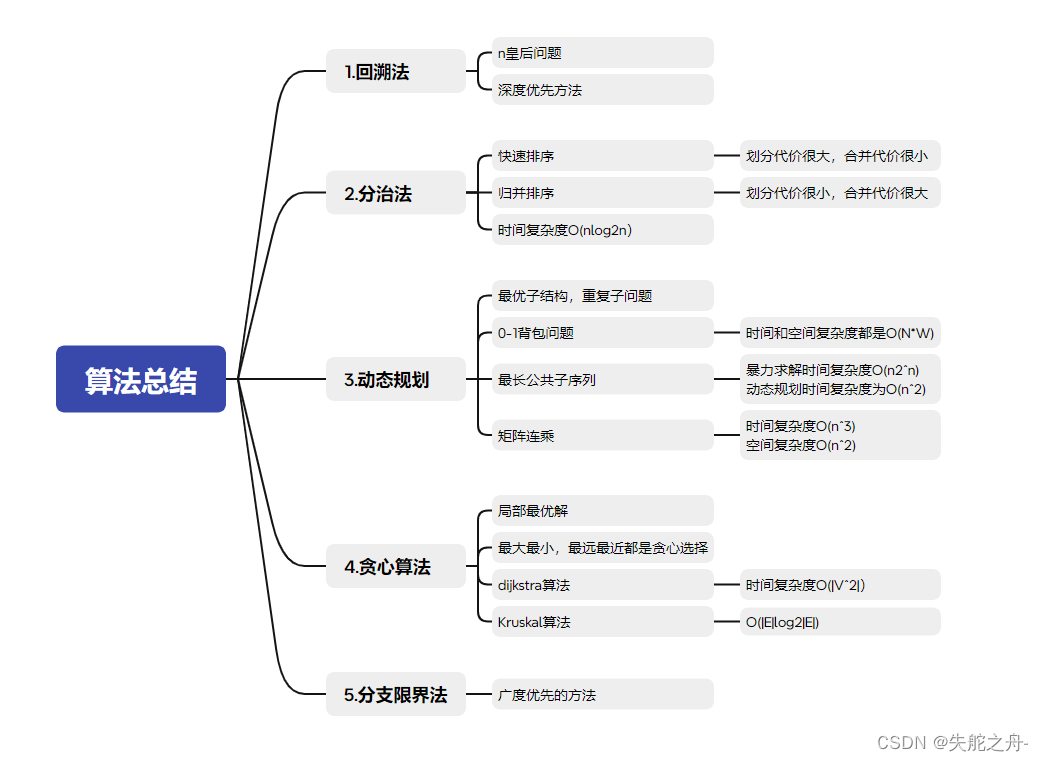
1 回溯法

深度优先方法搜索

1.1 n皇后问题

2 分治法

一般来说，分治算法在每一层递归上都有3个步骤
（1）分解将原问题分解成一系列子问题。
（2）递归地求解各子问题。
（3）若子问题足够小，则直接求解
（4）求解合并。将子问题的解合并成原问题的解。

大多数情况用递归来实现，但是不是一定

快速排序 划分代价很大，合并代价很小
归并排序相反
他们的时间复杂度都是O(nlog2n）

3 动态规划

最优子结构和重复子问题
自底向上方法计算最优值

3.1 0-1背包问题

时间和空间复杂度都是O(N*W)

分支限界法，回溯法,动态规划，这三种办法都可以处理0-1背包问题
贪心只能处理部分背包问题，不能处理0-1背包问题
贪心能够得到部分背包问题的最优解

3.2 最长公共子序列

暴力求解时间复杂度O($n{2}^n$)
动态规划时间复杂度为O(n^2)

3.3 矩阵连乘

时间复杂度O(n^3)
空间复杂度O(n^2)

4 贪心算法

局部最优
最大最小，最远最近都是贪心选择

dijkstra算法 时间复杂度O(|V^2|）
Kruskal算法 克鲁斯卡尔 O(|E|log2|E|) 适用于边稀疏

5 分支限界法

广度优先的方法搜索

---

总结

1.回溯法:深度优先
2.分支限界法:广度优先
3.贪心:局部最优
部分背包问题
4.动态规划:最优解
a. 01背包
b.公共子序列
C.矩阵连乘

这篇关于【中级软件设计师】上午题16-算法（应试考试简略版）的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---