本文主要是介绍轮子运动学约束,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
轮式机器人-多种轮子运动学约束
机器人运动学模型的第一步是表达加在单独轮子上的约束。正如在3.2.2节中所示那样,单独轮子的运动以后可以被联合起来计算整个机器人的运动。如在第2章所讨论那样,有四种基本的轮子类型,它们各具变化广泛的运动学参数。所以,我们一开始就要提出对各轮子类型特定的约束集合。
不过,有几个重要的假设会简化上述的陈述。我们假定轮子的平面总是保持垂直,且在所有的情况下,在轮子与地面之间只有一个单独的接触点。此外,我们假定在该单独的接触点无滑动。也就是说,轮子只在纯滚动和通过接触点绕垂直轴转动的条件下进行运动。对运动学更深人的处理,包括滑动接触,请参阅参考文献[25]。
在这些条件下,对每一个轮子类型,我们提出两个约束:
- 第一个约束坚持滚动接触的概念,即当运动在适当方向发生时,轮子必须滚动。
- 第二个约束坚持无横向滑动的概念,即在正交于轮子的平面,轮子必须无滑动。
固定的标准轮
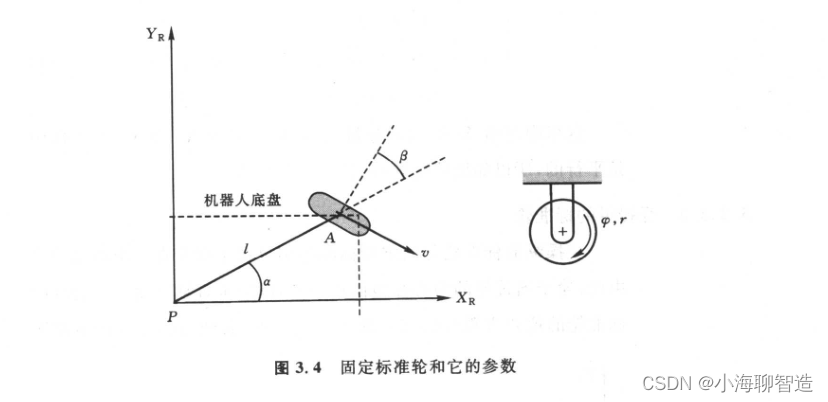
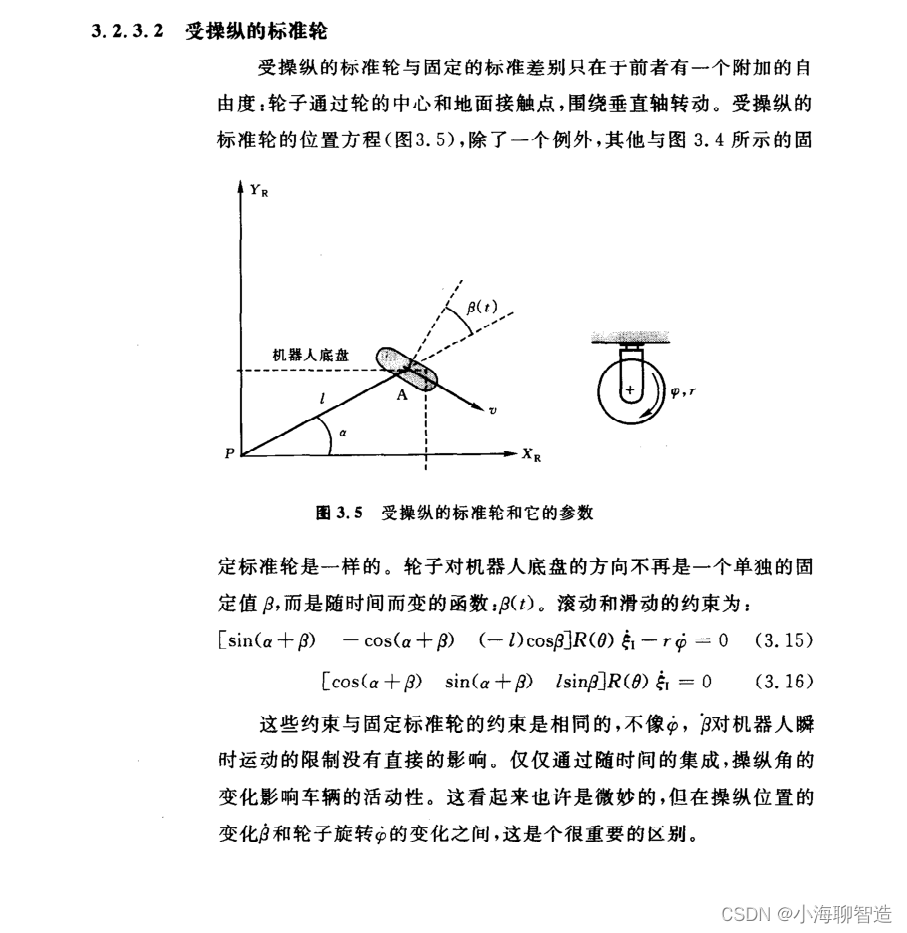
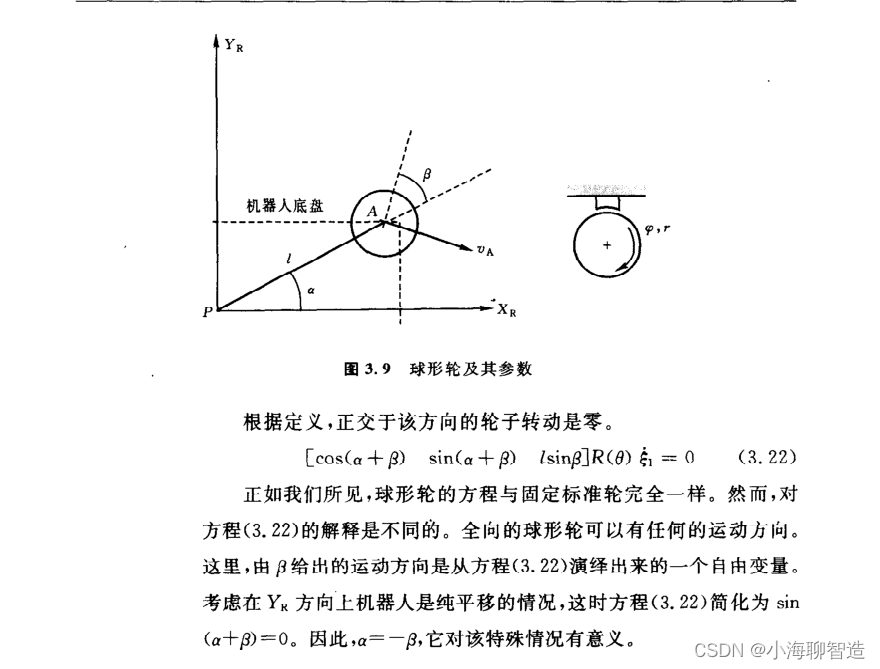
固定的标准轮没有可操纵的垂直转动轴。因此,它相对于底盘的角度是固定的,因而限制了沿轮子平面前后运动和围绕与地面接触点的转动。图3.4刻画了一个固定标准轮A,并说明了它相对于机器人局部参考框架{X,Y}的位置姿态。A的位置用极坐标中的距离l和角度a表示。轮子平面相对于底盘的角度用表示,因为固定标准轮是不可操纵的,所以B是固定的。具有半径r的轮子可随时转动,所以它围绕它的水平轴转动的位置是时间t的函数:&(t)







这篇关于轮子运动学约束的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!






