本文主要是介绍【刷题】最长回文子串——manacher(马拉车)算法,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
LeetCode 5.最长回文子串
给定字符串s,找到s中最长的回文子串。
回文串,指的是无论从左往右读还是从右往左读,结果都是一样的。
比如 “dabcbacf” 的最长回文子串为 “abcba”。
manacher算法
- 主要思路:充分利用前面已经求出的回文信息;
动态规划:
-
首先需要构建新的字符串,以消除奇回文串和偶回文串的差别,在每个字符间插入一个特殊符号(例如“#”),然后为了消除边界的影响,在开始和末尾各插入一个特殊字符(例如“$”和“0”);
-
列表p[i]存储以第i个字符为回文中心的回文半径;
-
动态维护max和id两个变量,max指前面所有回文所能到达的最右端位置,id指取max时的回文中心的位置;
-
o(n)复杂度
-
比如:
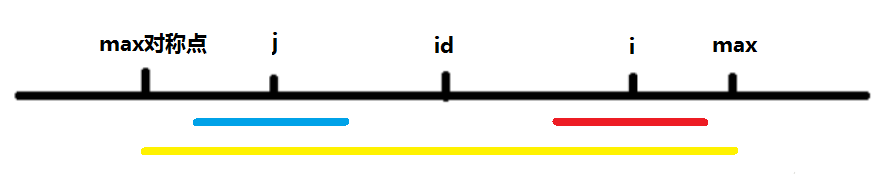
1) 首先明确,我们现在目的是求 i 位置的回文半径;
2)已知 id 位置回文是黄色部分,回文最右位置为 max ,则回文半径 p[id] 为 max-id ;
3)接下来是关键思路: i 关于 id 对称的位置是 j ,如果黄色部分是回文串,并且 j 的回文串为蓝色部分,那么对称过去的红色部分一定也为回文串!
4)比如‘sabacdffdcabar’(这里省略了添加特殊符号的步骤),对应的黄色部分是‘abacdffdcaba’,id 在第两个 f 之间,i 在第二个 b 的位置,i 关于 id 对称的位置 j 在第一个b的位置,j 的回文串是‘aba’,则 i 的回文串一定也是‘aba’!
5)至于超过红色的部分(也就是红色左边和红色右边)是不是回文串,需要进一步判断,向左向右依次比对即可,直到不相等中止;
6)要注意的点就是, max 与 i 的位置关系,如果前者大,那可以按照关键思路求解,如果后者大,则只能老办法,将回文半径初始化为1,以s[i]为中心向两边逐个检查;
7)还要注意 j 的回文半径与 max-i 的大小关系;p[i] 只能初始化为二者中较小的一个,因为如果前者大,则超过 max 的部分无法直接判断,如果后者大,才可以初始化为 j 的回文半径。
def manacher(string):s = '$#' + '#'.join([x for x in string]) + '#0'l = len(s)p = [0] * lmax_ = 0id_ = 0for i in range(l - 1):if max_ > i:p[i] = min(max_ - i, p[2 * id_ - i])else:p[i] = 1while s[i + p[i]] == s[i - p[i]]:p[i] += 1if i + p[i] > max_:max_ = i + p[i]id_ = imxr = max(p) - 1 # 最大回文长度ind = p.index(max(p))res = s[ind - mxr:ind + mxr + 1].replace('#', '') # 最长回文print(mxr)print(res)
LeetCode通过代码:
class Solution:def longestPalindrome(self, s: str) -> str:if not s:return ''ss = '$#' + '#'.join(s) + '#%'l = len(ss)p = [0 for _ in range(l)]id_ = 0max_ = 0for i in range(l - 1):if max_ > i:p[i] = min(max_ - i, p[2 * id_ - i])while ss[i + p[i] + 1] == ss[i - p[i] - 1]:p[i] += 1if i + p[i] > max_:max_ = i + p[i]id_ = imr = max(p)ind = p.index(mr)res = ss[ind - mr:ind + mr + 1].replace('#', '')return res
这篇关于【刷题】最长回文子串——manacher(马拉车)算法的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!








