本文主要是介绍0基础理解ECC并做题-攻防世界easy-ECC理解,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!



基点p就是最初选定的那个点


1和2都是整数集合,但是1/2=0.5就不属于整数集合

一直加,一直乘,还能保证有限个数字?这是因为采用了取模的运算,让元素始终都在有限的范围内。



如何计算分数求模?
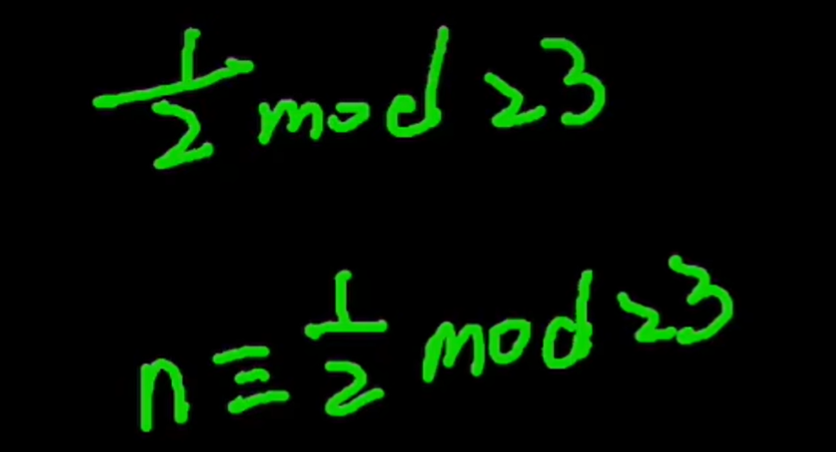
设n=1/2mod23,那么n和1/2mod23是同余的。而后两边同时乘2,就可以得到下面的内容。
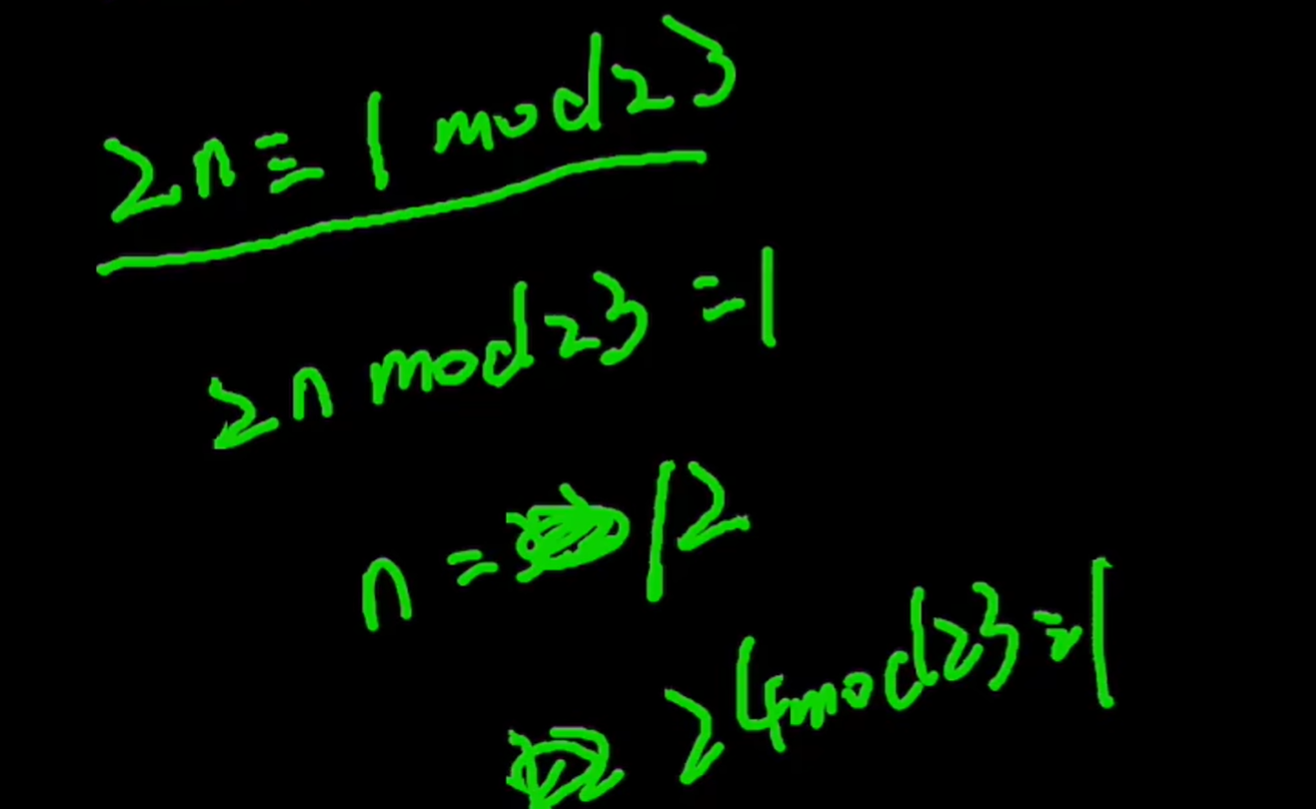
负数求模的算法

进而计算出2A的坐标,从而计算出3A,4A等等。
但是k那么大,这样计算岂不是很麻烦?
这时候我们就有了下面的计算方法

注意:这里算出二进制后,将其反转,也就是10010111反转一下是11101001 ,后面也就有了2^0+2^1+2^2+2^4+2^7
先算出A,然后取A的2倍,得到2A,而后2A+A,而后在2A的基础上再取2倍得到4A,而后再将A+2A+4A,再将4A取2倍,得到8A,那么就是A+2A+4A+8A,依次类推。这就是倍数加法运算。
例题:攻防世界:easy_ecc
附件内容

有p,a,b的数值,就可以知道这个椭圆曲线就是
y=x^3+ax+b=x^3+16546484x+4548674875 出发点G是(6478674857,5636379357093)
那么公钥我们设置为Q=k(x,y)=kG
先将K=546768进行二进制,二进制计算遵循原则:为从低位到高位依次处理二进制位,若位为0,则将当前点加倍;若位为1,则将当前点加倍后再与基点相加。
计算2A(只给了一个基点G,可以看出是A=B的类型),使用方法,即是公式:

解法1:脚本语言
class point:def __init__(self, x, y):self.x = xself.y = y
class ell:def __init__(self, p, a, b):self.p = pself.a = aself.b = bdef add(self, pA, pB):if pA.x == pB.x and pA.y == pB.y:k = mod((3 * (pA.x * pA.x) + self.a), (2 * pA.y), self.p)else:k = mod((pB.y - pA.y), (pB.x - pA.x), self.p)rx = k * k - pA.x - pB.xrx = rx % self.pry = k * (pA.x - rx) - pA.yry = ry % self.pR = point(rx, ry)return Rdef ne(self, n, G):s = str(bin(n)[::-1])print(s)sumG = NoneaddPoint = Gfor i in range(len(s)):if s[i] == '1':if sumG is None:sumG = addPointelse:#此处是用来计算SUMG的累加和sumG = self.add(sumG, addPoint)#无论是0还是1都加一次addPoint = self.add(addPoint, addPoint)return sumG
def mod(a, b, p):\# a/b mod pif b < 0:b = -ba = -areturn (a % p * pow(b, p - 2, p)) % p
p = 15424654874903
a = 16546484
b = 4548674875
ep = ell(p, a, b)
G = point(6478678675, 5636379357093)
k = 546768
flag = ep.ne(k, G)
print(flag.x + flag.y)
cyberpeace{19477226185390}解释一下代码:
初始化
__init__:用于初始化新创建的对象。class point:def __init__(self, x, y):self.x = xself.y = y
这里是定义了一个点,将传入的点(x,y)赋值给self.x和self.y核心关键
class ell:def __init__(self, p, a, b):self.p = pself.a = aself.b = bdef add(self, pA, pB):if pA.x == pB.x and pA.y == pB.y:k = mod((3 * (pA.x * pA.x) + self.a), (2 * pA.y), self.p)else:k = mod((pB.y - pA.y), (pB.x - pA.x), self.p)rx = k * k - pA.x - pB.xrx = rx % self.pry = k * (pA.x - rx) - pA.yry = ry % self.pR = point(rx, ry)return Rdef ne(self, n, G):s = str(bin(n)[::-1]) 10010111 -- 11101001print(s)sumG = None addPoint = G for i in range(len(s)): 1 1 1 0 1 0 0 1if s[i] == '1': if sumG is None: sumG = addPoint sumG:G else:#此处是用来计算SUMG的累加和sumG = self.add(sumG, addPoint) G+2G=3G 3G+4G=7G 7G+16G=23G 23G+128G=151G#无论是0还是1都自己加一次自己addPoint = self.add(addPoint, addPoint) 2G 2G+2G=4G 4G+4G=8G 16G 32G 64G 128G 256Greturn sumG
这里是定义了一个类ell,来完成一些列的操作。一点一点的看def __init__(self, p, a, b):self.p = pself.a = aself.b = b
初始化我们输入的p,a,b的数值。下面有个问题:这里的G点,也就是基点,到底是如何传进去的呢?def add(self, pA, pB):if pA.x == pB.x and pA.y == pB.y:k = mod((3 * (pA.x * pA.x) + self.a), (2 * pA.y), self.p)else:k = mod((pB.y - pA.y), (pB.x - pA.x), self.p)rx = k * k - pA.x - pB.xrx = rx % self.pry = k * (pA.x - rx) - pA.yry = ry % self.pR = point(rx, ry)return R
定义了一个加法规则,传入A,B两个点if pA.x == pB.x and pA.y == pB.y:如果A点和B点相同,也就是我们上面说的A=B的情况k = mod((3 * (pA.x * pA.x) + self.a), (2 * pA.y), self.p)
计算出k的数值,这里的mod方法使用的是后面定义的mod的计算方法
def mod(a, b, p):\# a/b mod pif b < 0:b = -ba = -a#pow() 函数用于计算 b 的 p - 2 次幂并取模 preturn (a % p * pow(b, p - 2, p)) % p这个Python函数mod(a, b, p)执行以下操作:实现a/b对模p进行计算。 检查除数的符号:如果b小于0,函数会将b和a都取其相反数。这是因为模运算中除数可以是负数,但在这个函数中,我们将其转换为正数以简化计算。 使用模逆元计算:函数使用了费马小定理的一个应用,即对于质数p,如果b与p互质(即它们的最大公约数为1),那么存在一个数x(即b^(p-2) % p),使得bx % p = 1。这个x被称为b关于模p的逆元。 计算模运算:通过(a % p) * (b^(p-2) % p),函数实现了a / b对模p的计算。这是因为a / b等价于a * (b^(-1)),而b^(-1)就是上面找到的模逆元。 最终取模:为了确保结果在0到p-1之间,函数对结果再次取模p。 总结来说,这个函数计算了a/b对模p的结果,其中b和p都是正整数,且p通常是一个质数,用于加密算法或者在有限域中进行计算。
else:k = mod((pB.y - pA.y), (pB.x - pA.x), self.p)
如果A,B两点不相同,执行上面的方法计算Krx = k * k - pA.x - pB.xrx = rx % self.pry = k * (pA.x - rx) - pA.yry = ry % self.pR = point(rx, ry)return R
得出K后,计算x和y的值,并返回这个坐标def ne(self, n, G):s = str(bin(n)[::-1])print(s)sumG = NoneaddPoint = Gfor i in range(len(s)):if s[i] == '1':if sumG is None:sumG = addPointelse:sumG = self.add(sumG, addPoint)addPoint = self.add(addPoint, addPoint)return sumG
推算出公钥Q,使用的就是倍数加法运算,将私钥K,代码里是n,k后面我们可以传入。s = str(bin(n)[::-1])print(s)将n转换为二进制字符串,并反转字符串,并输出一下s的数值。sumG = None设置sumG的初始值为空addPoint = G将输入的基点赋值给addPoint#循环遍历逆向输出的二进制数字
for i in range(len(s)):#如果二进制数字是1if s[i] == '1':#如果sumG还是空值的话if sumG is None:#将addPoint的数值赋予给sumGsumG = addPoint#sumG不是空数值的话else:#执行自加,这个函数的功能是将addPoint加到sumG上,并将结果赋值给sumGsumG = self.add(sumG, addPoint)#在每次循环中,无论当前位是 '1' 还是 '0',都使用 add 函数将 addPoint 自身相加一次(即 addPoint = self.add(addPoint, addPoint)),模拟点的倍增过程。addPoint = self.add(addPoint, addPoint)add 函数 功能说明:此函数实现的是椭圆曲线密码学中点的加法运算。给定椭圆曲线上两点 pA 和 pB,以及椭圆曲线方程的一些参数(隐含在类的属性中,如 self.a, self.p),计算这两点的和 R,结果同样位于同一条椭圆曲线上。 步骤分解: 判断特殊情况:首先检查 pA 和 pB 是否为同一点。如果是(即它们的坐标相同),根据椭圆曲线点加倍的公式计算斜率 k。公式为:[k = \text{mod}((3 \times (pA.x^2) + self.a), (2 \times pA.y), self.p)]。这里利用模运算保持结果在模 self.p 下。 常规情况处理:如果 pA 和 pB 不是同一个点,则按照点的加法规则计算斜率 k,公式为:[k = \text{mod}((pB.y - pA.y), (pB.x - pA.x), self.p)]。这同样确保了结果的正确性且在模意义下。 计算新点坐标: 根据 k 计算新点的 x 坐标 rx:[rx = k^2 - pA.x - pB.x],并取模 self.p 以确保结果落在期望的范围内。 接着计算 y 坐标 ry:[ry = k \times (pA.x - rx) - pA.y],同样对结果取模 self.p。 构造并返回新点:最后,使用计算出的 rx 和 ry 创建一个新的点 R 并返回。 ne 函数 功能说明:此函数实现了在椭圆曲线上通过多次点加操作计算一个点乘(即点 G 重复相加 n 次)的结果。这是椭圆曲线加密算法中的关键步骤,用于高效地计算大指数幂的点表示。 步骤分解: 转换整数为二进制:将输入的整数 n 转换为二进制字符串 s,并反转字符串以便从最低位开始处理。 初始化变量:设置 sumG 初始化为 None,表示累加结果的初始状态;addPoint 初始化为给定点 G,作为每次迭代中用于加法操作的基础点。 遍历二进制字符串:从最低位到最高位遍历二进制字符串 s 的每个字符。 对于遇到的每一个 '1',执行以下操作: 如果 sumG 仍为 None,则将其设为 addPoint。 否则,使用 add 函数将 sumG 与 addPoint 相加,并更新 sumG 为结果。 在每次循环中,无论当前位是 '1' 还是 '0',都使用 add 函数将 addPoint 自身相加一次(即 addPoint = self.add(addPoint, addPoint)),模拟点的倍增过程。 返回结果:遍历结束后,sumG 即为点 G 乘以 n 的结果,在椭圆曲线上的表示,最终返回 sumG。 综上,这两个函数共同实现了椭圆曲线上的点加法和点乘运算,是椭圆曲线密码学中的基础算子。
解法2:工具:ECCTOOL
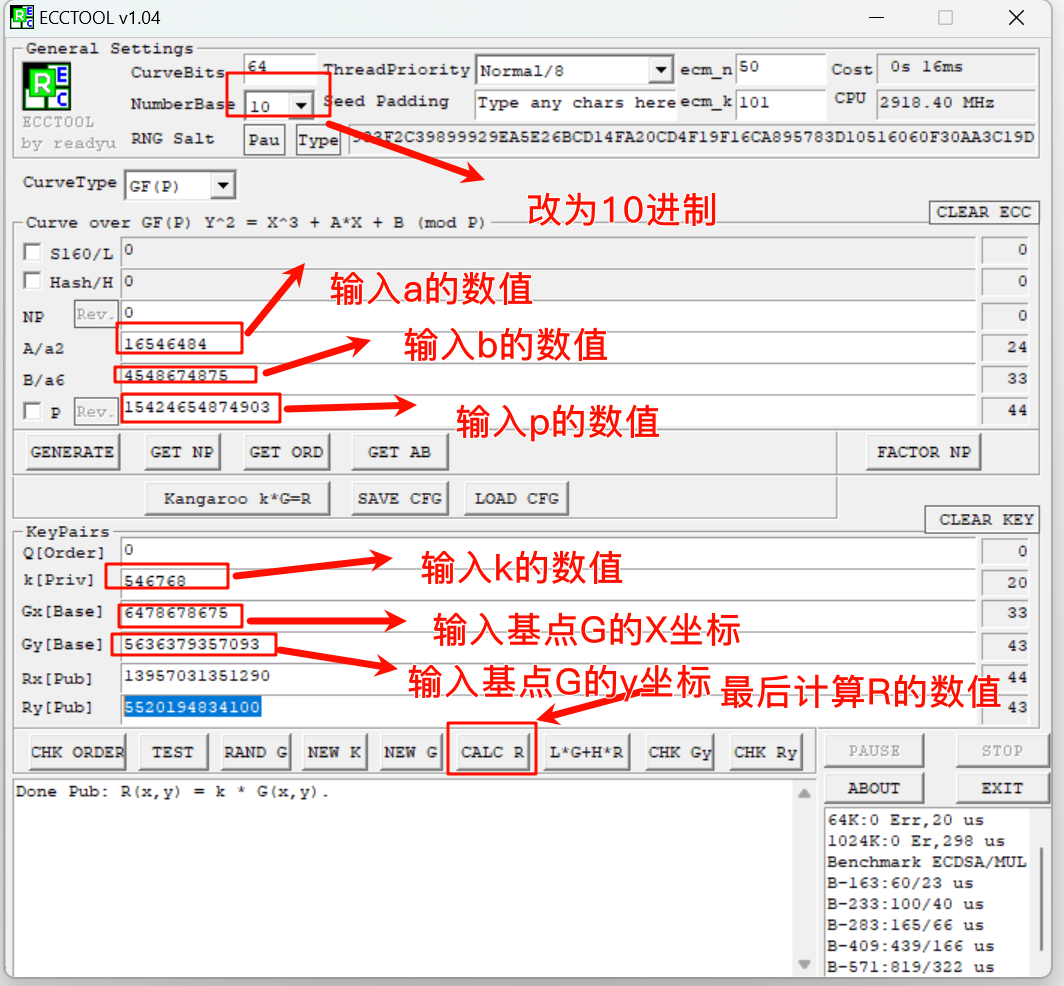
最后将Rx和Ry的数值相加就是flag
这篇关于0基础理解ECC并做题-攻防世界easy-ECC理解的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!





