本文主要是介绍KAN网络,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
目录
背景知识
什么是神经网络?
神经网络发展史
MP神经元模型
感知机模型
KAN
引言
MLP架构vsKAN架构
从数学定理方面来看:
从算法层面上看:
从实际应用过程看:
KAN的架构细节
KAN的准确性
KAN的可解释性
监督学习
无监督学习
数学领域
物理领域
自动和手动模式的比较
何时该选用 KAN?
背景知识
什么是神经网络?
神经网络是一种模仿生物神经网络结构和功能的非线性数学模型

神经网络发展史

MP神经元模型
当前神经元会收到x1到xn传来的信号,这些输入信号会通过w1到wn的权重,与当前神经元进行连接,从而传递信息。

感知机模型

KAN
引言
弗拉基米尔·阿诺德和安德烈·科尔莫戈罗夫证明了,如果f是有界域上的多变量连续函数,则f可以写成单变量连续函数和加法二元运算的有限组合。
即“任何一个多变量连续函数都可以表示为一些单变量函数的组合”

KAN 的名字也由此而来。
正是受到这一定理的启发,研究人员用神经网络将 Kolmogorov-Arnold 表示参数化。
为了纪念两位伟大的已故数学家 Andrey Kolmogorov 和 Vladimir Arnold,我们称其为科尔莫格罗夫-阿诺德网络(KANs)。
MLP架构vsKAN架构
跟 MLP 最大、也是最为直观的不同就是,MLP 激活函数是在神经元上,而 KAN 把可学习的激活函数放在权重上。
从数学定理方面来看:
MLP 的灵感来自于通用近似定理,即对于任意一个连续函数,都可以用一个足够深的神经网络来近似。
而 KAN 则是来自于 Kolmogorov-Arnold 表示定理 (KART),每个多元连续函数都可以表示为单变量连续函数的两层嵌套叠加。
从算法层面上看:
MLPs 在神经元上具有(通常是固定的)激活函数
而 KANs 在权重上具有(可学习的)激活函数。这些一维激活函数被参数化为样条曲线。
从实际应用过程看:
KAN 可以直观地可视化,提供 MLP 无法提供的可解释性和交互性。

KAN的架构细节

左侧的图显示了 KAN 的分层架构。每层包括一组节点,每个节点都通过一组特定的函数处理输入数据,输出到下一层。每个节点上的小图标表示的是激活函数的形式,这里用B-样条函数作为激活函数。
右侧的图展示了一个激活函数 ϕ(x),它被参数化为一个B-样条函数。图中还展示了如何通过改变B-样条的节点(也称为控制点)数量来调整函数的粒度。
这张图的核心在于展示KAN如何通过使用B-样条作为激活函数,结合网络的多层结构和激活函数的动态调整(网格扩展技术),来处理复杂的高维数据。这种设计使得网络不仅能适应不同的数据分辨率,还能通过调整激活函数的精度来优化性能。
KAN的准确性
神经缩放规律:KAN 的缩放速度比 MLP 快得多。除了数学上以 Kolmogorov-Arnold 表示定理为基础,KAN 缩放指数也可以通过经验来实现。

函数拟合:KAN 比 MLP 更准确。
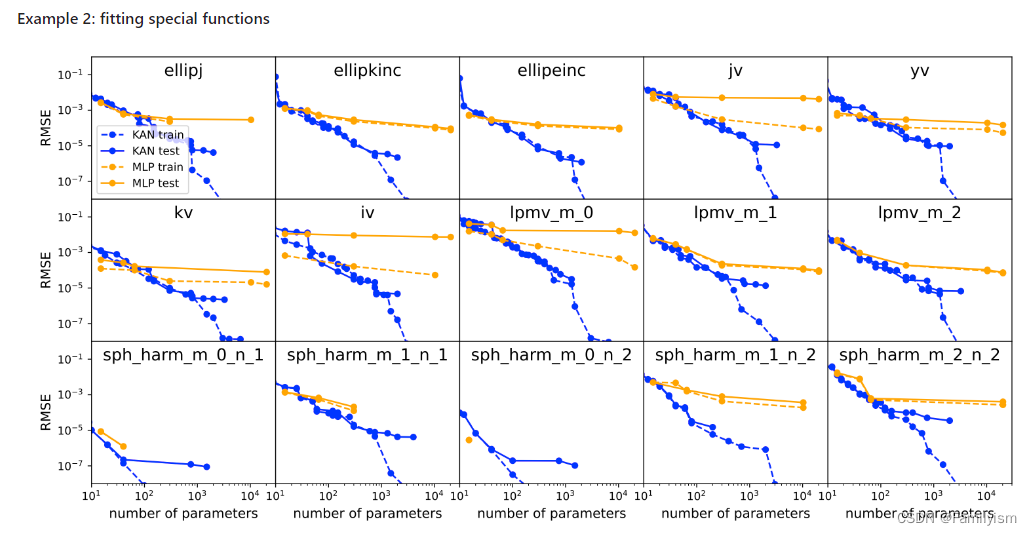
偏微分方程求解:比如求解泊松方程,KAN 比 MLP 更准确。
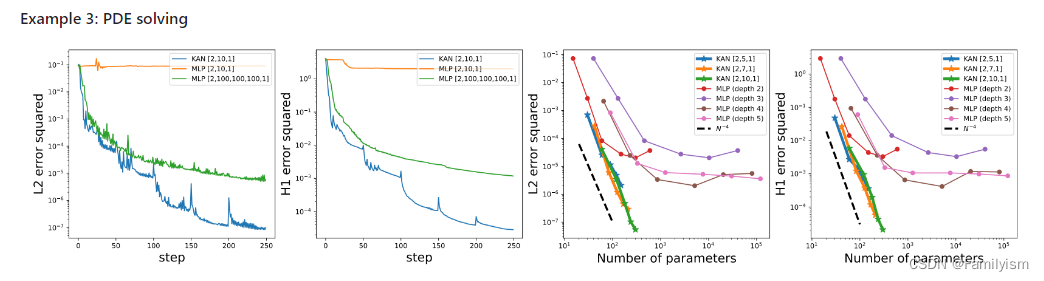
规避灾难性遗忘:KAN 不会像 MLP 那样容易灾难性遗忘,它天然就可以规避这个缺陷。

KAN的可解释性
监督学习
在可解释方面,KAN 能通过符号公式揭示合成数据集的组成结构和变量依赖性。

无监督学习

在无监督学习中,目标是识别数据中变量之问的依赖关系,而不是预测输出,KANS通过修改其结构,能够识别哪些输入变量是相互依赖的。左图(seed=0)和右图(seed =2024)显示了相同的数据集但不同的初始化种子如何导致KAN 学到不同的依赖关系结构。 KAN 通过其灵活的网络结构捉供了一种强大的工具来探索这些关系,从而增强了模型的解释性和应用的广泛性
数学领域

用KAN来解决结点理论问题: 图a显示使用 17 个变量的网络结构实现了81.6%的测试准确率。仅使用3个最重要的变量精简后的模型达到了78.2%的测试准确率。图(c)通过饼图展示了三个变量对预测结果的贡献比例。
物理领域

本文用KAN来探索和解释物理模型中的动力学边界,尤其是在量子系统的安德森局域化现象中的应用
自动和手动模式的比较
人类用户可以与 KANs 交互,使其更具可解释性。在 KAN 中注入人类的归纳偏差或领域知识非常容易。

何时该选用 KAN?

关于这个问题,主要看想要的是什么?如果效率优先,也就是最右边这条支路,选MLP,因为目前,KANS训练速度较慢是其主要瓶颈,通常比 MLPS慢10倍。但如果想要小模型,KAN更好。如果可解释性优先,选中间,那么KAN牛遍。如果准确性优先,最左边,KAN 也更牛通,尽管 KAN 显示了不错的前景,但毕竟刚开始,还很不足。
这篇关于KAN网络的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!








