031.下一个排列Java实现

本文主要是介绍031.下一个排列Java实现，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

题意

 

整数数组的一个 排列 就是将其所有成员以序列或线性顺序排列。

 

例如，arr = [1,2,3] ，以下这些都可以视作 arr 的排列：[1,2,3]、[1,3,2]、[3,1,2]、[2,3,1] 。

 

整数数组的 下一个排列 是指其整数的下一个字典序更大的排列。更正式地，如果数组的所有排列根据其字典顺序从小到大排列在一个容器中，那么数组的 下一个排列 就是在这个有序容器中排在它后面的那个排列。

 

如果不存在下一个更大的排列，那么这个数组必须重排为字典序最小的排列（即，其元素按升序排列）。

 

1. 例如，arr = [1,2,3] 的下一个排列是 [1,3,2] 。
2. 类似地，arr = [2,3,1] 的下一个排列是 [3,1,2] 。
3. 而 arr = [3,2,1] 的下一个排列是 [1,2,3] ，因为 [3,2,1] 不存在一个字典序更大的排列。

 

给你一个整数数组 nums ，找出 nums 的下一个排列。

 

必须 原地 修改，只允许使用额外常数空间。

 

难度

 

中等

 

示例

例1

 

输入：nums=[1,2,3]

输出：[1,3,2]

输入：nums=[3,2,1]

输出：[1,2,3]

输入：nums=[1,1,5]

输出：[1,5,1]

 

分析 1

 

这道题看起来很唬人，比如题目描述中提到的“字典序”，很多人第一眼看到这个名词的时候会有点懵，这里简单解释一下。

 

字典序（dictionary order），又称 字母序（alphabetical order），原意是表示英文单词在字典中的先后顺序，在计算机领域中扩展成两个任意字符串的大小关系。

 

在这道题目中，字典序其实是指☞ 数字大小的先后顺序。

 

理解了“字典序”，就能很快理解这道题的题意了：要我们求出比这个数更大的一个排列，比如 123，比它大的是 132，对吧？只需要改变 23 的位置就可以了。312 也比 123 大，只不过它是比 132 更大的一个，不是比 123 更大的一个，官大一级压死人，一级一级来压（😂）。

就好像我们在打扑克牌，我出了一个对 10，那你出对 11 就压住我了，没必要把手里的对 12 先出来，对吧？

 

再比如 321 已经是「1、2、3」 这三个数字组合中最大的那个了，那就等于说没有更大的了，所以返回 123 这个最小的。

 

明白了吧？

 

要想解题，首先得明白题意，所以语文理解是非常重要的，其次是经验（😁）。

 

那凭借我们以往的经验，可能一下子会想到全排列。就拿 1、2、3、4 来举例吧，全排列如下：

nums=[1,2,3,4]

nums=[1,2,4,3]

nums=[1,3,2,4]

nums=[1,3,4,2]

nums=[1,4,2,3]

nums=[1,4,3,2]

nums=[2,1,3,4]

nums=[2,1,4,3]

nums=[2,3,1,4]

nums=[2,3,4,1]

nums=[2,4,1,3]

nums=[2,4,3,1]

nums=[3,1,2,4]

nums=[3,1,4,2]

nums=[3,2,1,4]

nums=[3,2,4,1]

nums=[3,4,1,2]

nums=[3,4,2,1]

nums=[4,1,2,3]

nums=[4,1,3,2]

nums=[4,2,1,3]

nums=[4,2,3,1]

nums=[4,3,1,2]

nums=[4,3,2,1]

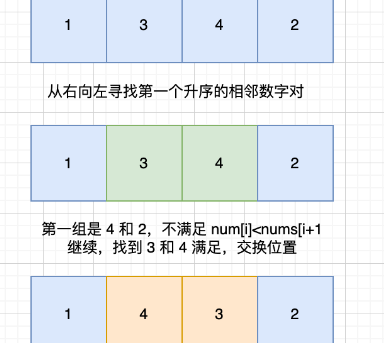
观察nums = [1,3,4,2] -> nums = [1,4,2,3]这一步，因为4比3大，且4的位置在3之后，所以将4与3交换，必然能够使得nums变大，交换了之后，则变成了nums = [1,4,3,2]。

 

但显然这不是最小的比nums = [1,3,4,2]大的一个排列，我们还要把3和2的位置再翻转一下，才能得到nums = [1,4,2,3]这个 恰好 比nums = [1,3,4,2]大一点的排列。

 

那到底该怎么去找到这个 恰好 比nums大一点的排列呢？

第一步，我们可以从右向左查找第一个升序的相邻数字对 (i, i+1)，满足 nums[i] < nums[i+1]。

 

这意味着从 i+1 到末尾的数字都是降序的。如果找不到这样的 i（即整个数组是降序的），这说明当前排列已经是最大的排列，我们只需将其翻转为最小排列即可。

这一步完成之后，并不能保证我们得到的排列就是 恰好 比nums大一点的排列。

这一步完成之后，并不能保证我们得到的排列就是 恰好 比nums大一点的排列。

 

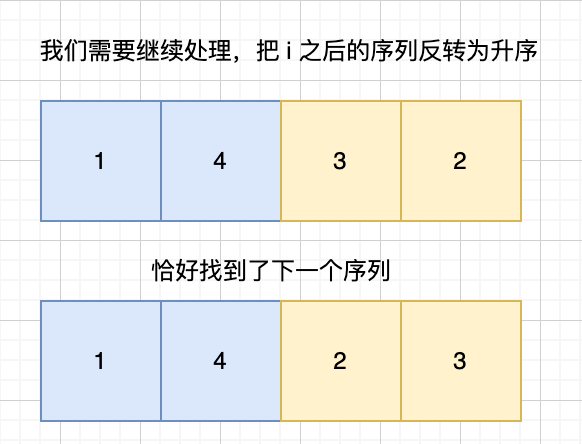
第二步，我们还要对nums[i+1] 到 nums[nums.length - 1]这个区间进行翻转，使得它变成升序排列，这样才能得到 恰好 比nums大一点的排列。

 

比如说上面提到的 [1,4,3,2]，i+1（i=1）到末尾的部分是 32。这部分是降序的。为了得到下一个排列，我们需要这部分变成升序。我们需要将这部分翻转，变成 23。

所以到这里，这道题目就迎刃而解了。具体代码实现：

class Solution {public void nextPermutation(int[] nums) {// 步骤1：从右向左查找第一个升序的相邻数字对(i, i+1)，满足nums[i] < nums[i+1]。int i = nums.length - 2;while (i >= 0 && nums[i] >= nums[i + 1]) {i--;}if (i >= 0) {// 步骤2：在nums[i+1:]中从右向左找到第一个大于nums[i]的数字nums[j]。int j = nums.length - 1;while (j >= 0 && nums[i] >= nums[j]) {j--;}// 步骤3：交换nums[i]和nums[j]。swap(nums, i, j);}// 步骤4：将nums[i+1:]翻转，使其变为升序。reverse(nums, i + 1);}// 用于交换数组中两个元素的位置private void swap(int[] nums, int i, int j) {int temp = nums[i];nums[i] = nums[j];nums[j] = temp;}// 用于将数组的一部分翻转，即将nums[start:]变为升序private void reverse(int[] nums, int start) {int end = nums.length - 1;while (start < end) {swap(nums, start, end);start++;end--;}}
}

为了更清晰地理解题解代码，我们将其拆分成几个关键部分，并逐一说明每部分的作用和逻辑。

 

1.寻找升序对 (i, i+1)

int i = nums.length - 2;
while (i >= 0 && nums[i] >= nums[i + 1]) {i--;
}

1. 目的：从数组的右端开始向左扫描，寻找第一个升序的相邻数字对，即找到第一个nums[i] < nums[i + 1]的位置。这个位置i是需要进行调整的起点，因为nums[i]右边的序列是降序的，没有更大的排列空间。
2. 逻辑：使用一个while循环从右向左遍历数组，直到找到满足升序条件的i。

 

2.在 nums[i+1:] 中找到第一个大于 nums[i] 的数字并交换

 

nums[i+1:] 是指从i+1到数组末尾的部分。

if (i >= 0) {int j = nums.length - 1;while (j >= 0 && nums[i] >= nums[j]) {j--;}swap(nums, i, j);
}

1. 目的：如果找到了这样的i，则在其右侧找到第一个大于nums[i]的数字nums[j]，然后交换nums[i]和nums[j]。这一步是为了在当前排列的基础上得到下一个稍大的数字。
2. 逻辑：通过向左扫描数组的剩余部分来查找j，一旦找到就执行交换。

 

3.翻转 nums[i+1:] 使其升序

reverse(nums, i + 1);

1. 目的：交换nums[i]和nums[j]后，i之后的序列仍然保持降序。为了获得下一个排列，需要将这个序列翻转成升序，这样从i+1到数组末尾就构成了最小的排列，确保整个数组是下一个更大的排列。
2. 逻辑：从i+1开始到数组末尾，执行翻转操作，使其成为升序。

 

4.交换方法 swap

private void swap(int[] nums, int i, int j) {int temp = nums[i];nums[i] = nums[j];nums[j] = temp;
}

交换数组中两个位置的元素。

 

5.翻转方法 reverse

private void reverse(int[] nums, int start) {int end = nums.length - 1;while (start < end) {swap(nums, start, end);start++;end--;}
}

将数组从指定位置start到数组末尾的部分翻转，使其成为升序。

测试：

/*** @ClAssName NextPermutation* @Description* 输入：nums=[1,2,3]* 输出：[1,3,2]* 输入：nums=[3,2,1]* 输出：[1,2,3]* 输入：nums=[1,1,5]* 输出：[1,5,1]* @Author 欧妮甲是神仙* @Date 2024/5/11 17:{MINUTE}*/
public class NextPermutation {public static void main(String[] args) {int[] nums = {1,3,4,2};nextPermutation(nums);System.out.println(Arrays.toString(nums));}static void  nextPermutation(int[] nums){//1、从右向左查找到第一个升序的相邻数字（i， i+ 1） ，满足 nums[i] < nums[i +1] .//那么一直找的条件是 反过来的， num[i]  > num[i +1]int i = nums.length -2;   ///表示倒数第二个数 ，如果为倒数第一个数， nums[i] >= nums[i+1] ，这里会数组越界while (i >=0 && nums[i] >= nums[i+1]){i--;}//找到定位的i之后if (i >=0){//2、在num[i+1]中从右向左找到第一个大于num[i]的数字num[j].。int j = nums.length-1;while (j >=0 && nums[i] >=nums[j]){j--;}//3、交换num[i]和num[j]swap(nums ,i , j);}//4、将num[i+1]翻转，使其变为升序revers(nums , i +1);}private static void  swap(int[] nums, int i, int j){int temp = 0;temp = nums[i];nums[i] = nums[j];nums[j] = temp;}//用于将数组的一部分翻转，即将nums[start] 变为升序private static void  revers(int[] nums, int start){int end = nums.length-1;while (start < end){swap(nums , start ,end);start++;end--;}}}

 

效率嘛，自然是快得飞起。

总结

 

这道题目的难点其实在于字典序的理解，一旦理解之后，整个题目的解法就不算是特别难了。

题目链接地址：

. - 力扣（LeetCode）

这篇关于031.下一个排列Java实现的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---