本文主要是介绍【智能算法】正切搜索算法(TSA)原理及实现,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
目录
- 1.背景
- 2.算法原理
- 2.1算法思想
- 2.2算法过程
- 3.结果展示
- 4.参考文献
- 5.代码获取
1.背景
2022年,A Layeb受到正切函数启发,提出了正切搜索算法(Tangent Search Algorithm, TSA)。


2.算法原理
2.1算法思想
TSAT基于正切函数的数学模型将给定的解决方案移动到更好的解决方案,提出了切线飞线函数,其具有平衡开发与勘探搜索的优点。
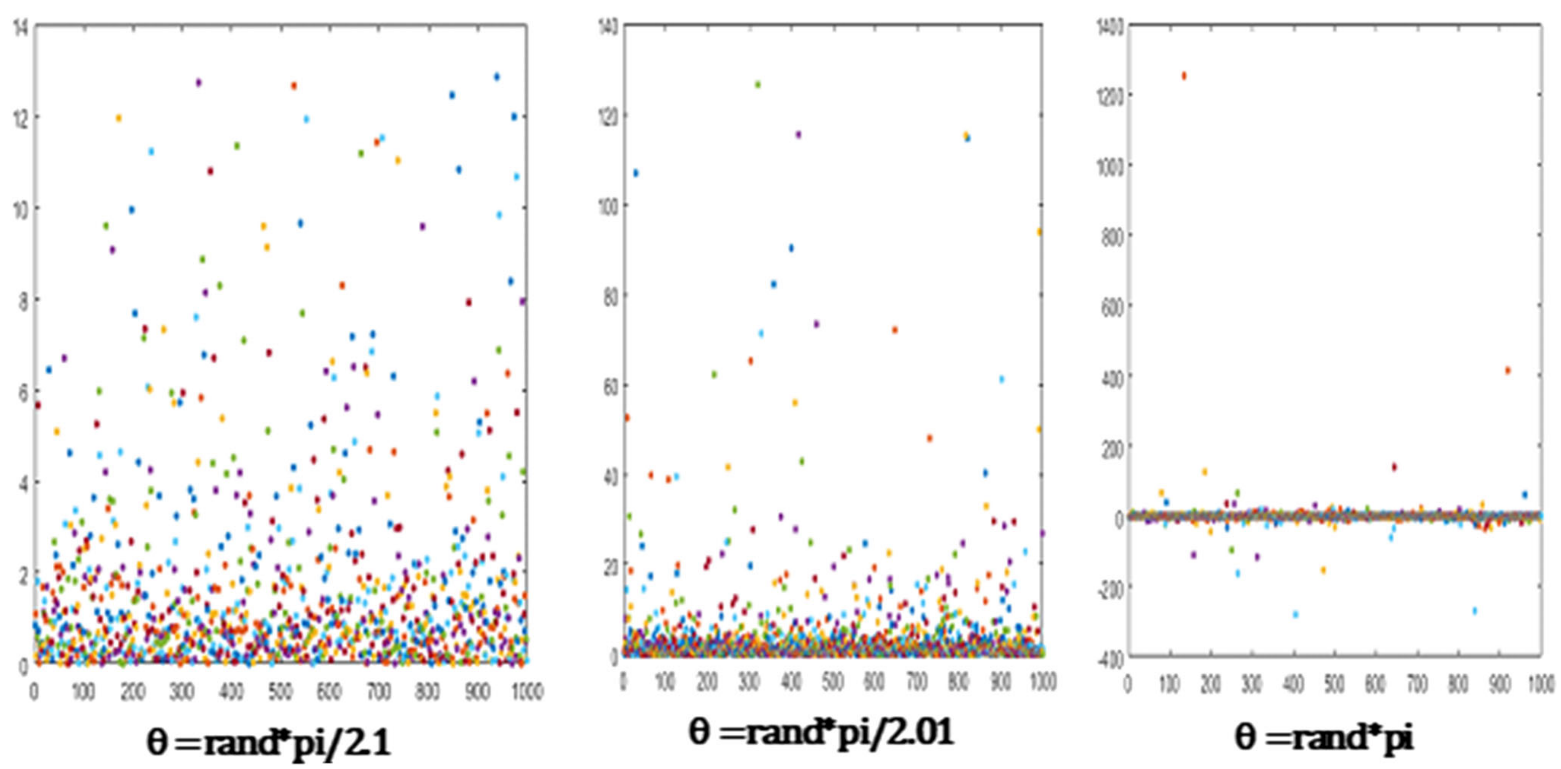
在TSA中,所有的运动方程都由一个全局阶跃控制,其形式为 s t e p ∗ t a n ( θ ) step*tan(\theta) step∗tan(θ),类似于levy飞行函数,称为正切飞行。
无论是基于导数还是无导数的最优算法都是基于如下的下降方程:
X t + 1 = X t + step ∗ d (1) X^{t+1}=X^t+\text{ step}*d\tag{1} Xt+1=Xt+ step∗d(1)
其中step是移动的大小,d是移动的方向。
切线飞行乘以一个递减对数函数的行为。探索搜索在早期迭代中很大,在最后迭代中减少。TSA由三个主要部分组成:强化搜索、探索搜索和逃离局部最小。探索阶段的目的是很好地探索搜索空间并找到最有希望的候选对象。而强化分量则用于将搜索过程导向种群中当前的最佳解。最后,在随机搜索代理(解)的每次迭代中应用逃离局部最小值过程,以避免陷入局部最小值。
2.2算法过程
强化搜索
在强化搜索中,TSA首先进行随机局部行走,然后将得到的解中的一些变量替换为当前最优解中对应变量的值。对于大于4的问题,替换变量的比例等于20%,对于小于或等于4个变量的问题,替换变量的比例等于50%。
X i t + 1 = X i t + s t e p ∗ tan ( θ ) ∗ ( X i t − o p t S i t ) X i t + 1 = o p t S i t if variable i is selected (2) X_i^{t+1}=X_i^t+step*\tan(\theta)*\left(X_i^t-optS_i^t\right)\\X_i^{t+1}=optS_i^t\text{ if variable i is selected}\tag{2} Xit+1=Xit+step∗tan(θ)∗(Xit−optSit)Xit+1=optSit if variable i is selected(2)
探索搜索
TSA使用变步长与切线飞行的乘积来进行全局随机游动。正切函数有助于有效地探索搜索空间。h接近于/2会使正切值变大,得到的解会远离当前解,而h接近于0会使正切函数的值变小,得到的解会接近当前解。因此,探索搜索方程在全局随机漫步和局部随机漫步之间合并。将探索搜索方程应用于每个变量,其概率为1/D,其中D为问题的维度。
X i t + 1 = X i t + s t e p ∗ tan ( θ ) (3) X_i^{t+1}=X_i^t+\mathrm{step}*\tan(\theta)\tag{3} Xit+1=Xit+step∗tan(θ)(3)
强化搜索和探索搜索是根据给定的概率进行的,称为Pswitch。

逃离局部最小
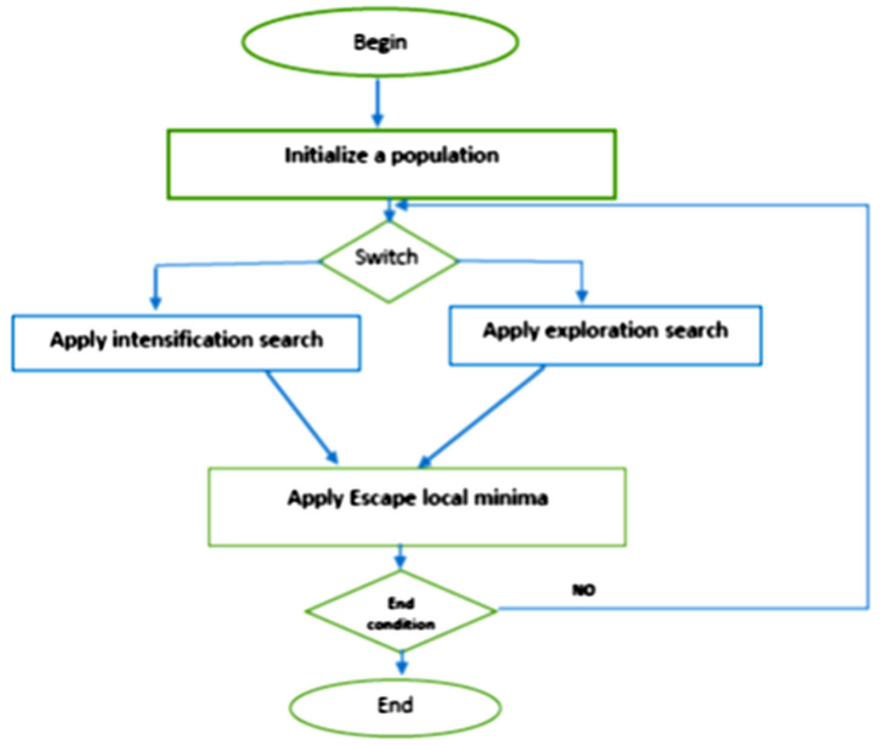
为了避免局部最小停滞问题,TSA采用了一种机制通过使用如图所示的特定程序来处理这个问题,这个过程有两个部分以一定的概率执行。
X = X + R . ∗ ( o p t S − r a n d ∗ ( o p t S − X ) ) X = X + tan ( tan ) ∗ ( u b − l b ) (4) \begin{aligned}&X =X + R.*(\mathrm{opt}S- \mathrm{rand}*(\mathrm{opt}S-X))\\&X = X+ \tan(\tan)*(\mathrm{ub}-\mathrm{lb})\end{aligned}\tag{4} X=X+R.∗(optS−rand∗(optS−X))X=X+tan(tan)∗(ub−lb)(4)

与许多优化算法相比,TSA使用的参数较少,Pswitch, Pesc和step, h是强调开发和探索搜索的主要参数。TSA在早期采用较大的步长,随着搜索过程的进行,步长在迭代过程中呈非线性减小。切线飞行除了对步长有很大的影响外,还使其具有振荡性和周期性。为了适应挖掘和强化搜索过程,TSA采用了基于对数函数的自适应步长非线性递减格式。TSA使用两种步长变量,在强化搜索中使用第一个步长变量:
s t e p 1 = 10 ∗ s i g n ( r a n d − 0.5 ) ∗ n o r m ( o p t S ) ∗ l o g ( 1 + 10 ∗ dim / t ) (5) \begin{array}{c}\mathrm{step}1=10*\mathrm{sign}(\mathrm{rand}-0.5)*\mathrm{norm}(\mathrm{opt}S)*\mathrm{log}(1+10*\dim/t)\end{array}\tag{5} step1=10∗sign(rand−0.5)∗norm(optS)∗log(1+10∗dim/t)(5)
在探索搜索中,步长为:
s t e p 2 = 1 ∗ s i g n ( r a n d − 0.5 ) ∗ n o r m ( o p t S − X ) / l o g ( 20 + t ) (6) \begin{aligned}\mathrm{step}2=1*\mathrm{sign}(\mathrm{rand}-0.5)*\mathrm{norm}(\mathrm{opt}S-X)/\mathrm{log}(20+t)\end{aligned}\tag{6} step2=1∗sign(rand−0.5)∗norm(optS−X)/log(20+t)(6)
norm()是欧几里得范数,X是当前解,optS是当前最佳解,用于引导搜索过程走向最佳解。
流程图
3.结果展示
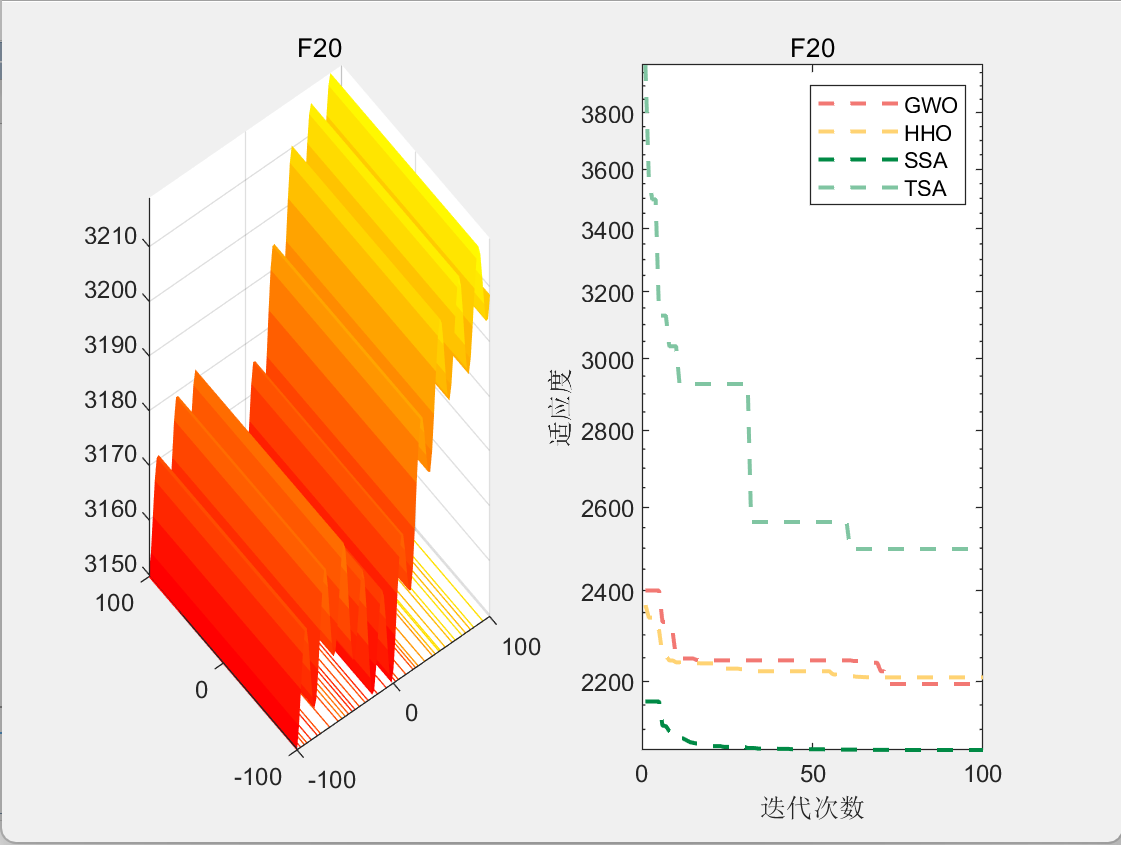
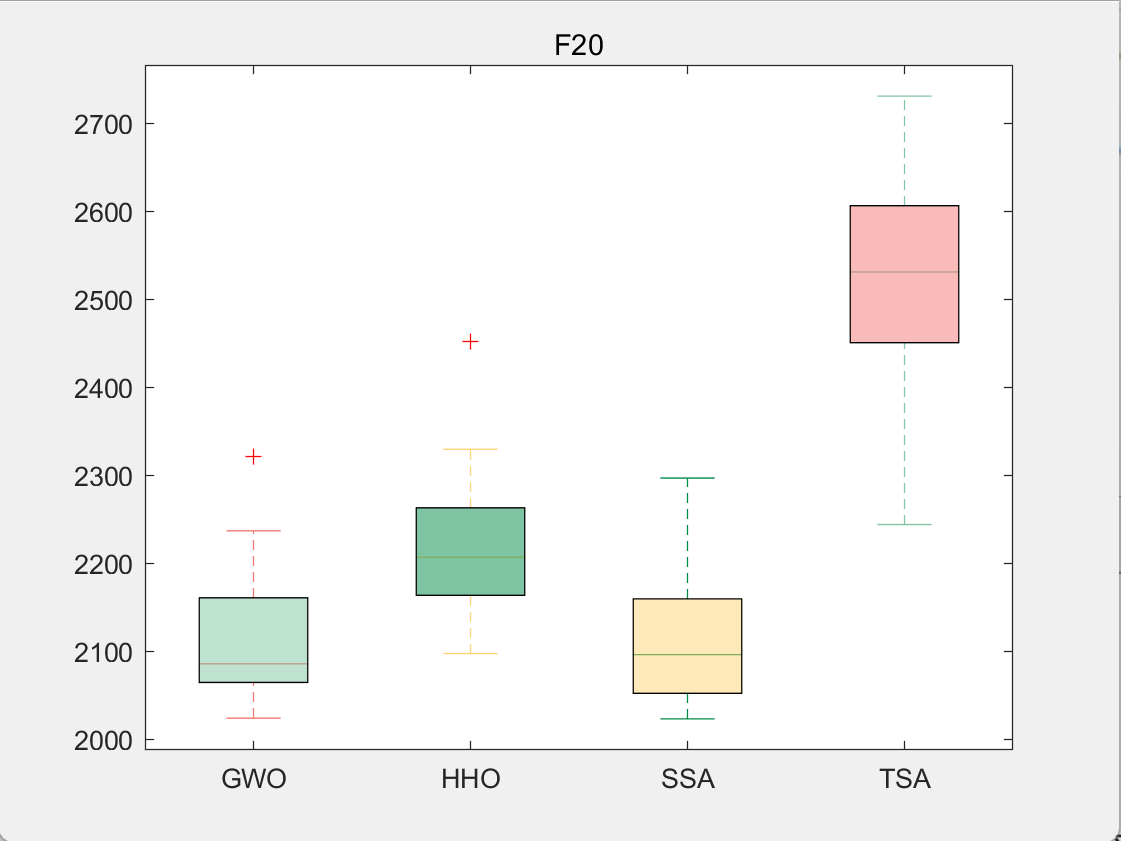
使用测试框架,测试TSA性能 一键run.m
- 【智能算法】省时方便,智能算法统计指标——一键运行~
CEC2017-F20

4.参考文献
[1] Layeb A. Tangent search algorithm for solving optimization problems[J]. Neural Computing and Applications, 2022, 34(11): 8853-8884.
5.代码获取
这篇关于【智能算法】正切搜索算法(TSA)原理及实现的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!






