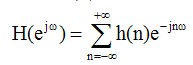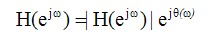本文主要是介绍相位特性解卷绕，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！
1.什么是解卷绕？为什么要解卷绕？
对于FIR滤波器的系数，也就是FIR滤波器的单位冲击响应，做离散时间的傅里叶变换。比如，像下面这样。
所得到的结果是这个FIR滤波器的频率响应。然而，频率响应又表示为振幅特性和相位特性，就像这样
所以，振幅特性和相位特性就按下式可以计算出来。
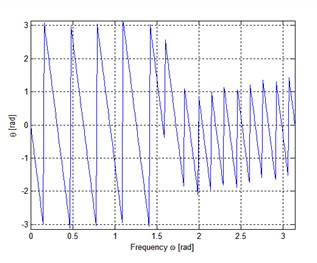
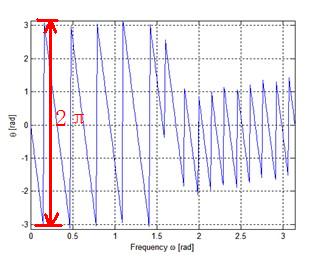
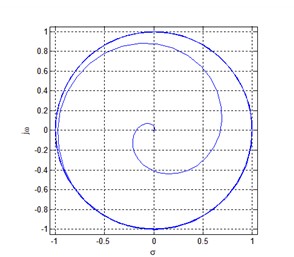
既然如此，我们就把一个系统的相位特性作图，看看得到的是什么东西。就拿我们之前已经设计并实现的FIR来做试验，其相位特性如下图所示。
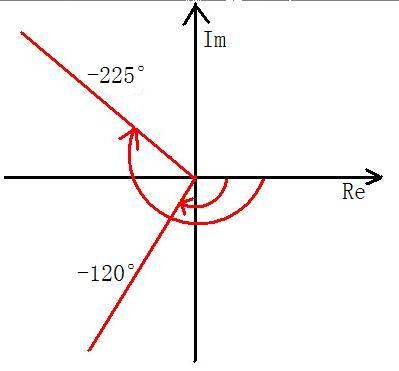
我们都知道，FIR滤波器是具有线性相位特性的，说的不严格一点，至少他是一条直线。而上图的拿Matlab画的相位特性，并是这样的。为什么呢？再次看看我们之前的算式，其使用到了反正切函数。假设，我们现在所设计的滤波器某一段相位特性，是由-120°转动到-225°的，就像下图所示一样的。
但是，Matlab所求得的反正切的值的范围是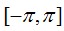
这也就解决了一个问题，为什么明明是线性相位特性，用Matlab画出来的相位特性却如此不规则。所以，在这个时候，我们需要把反正切漏算的2π给补上，这个过程就叫做解卷绕，有的也称为解包裹。在Matlab中，使用函数unwrap()进行解卷绕操作，具体的代码就像这样。当然，在绘制相位特性前，你需要一组FIR滤波器系数h。
- w = 0:0.01:pi;
- H = freqz(h,1,w);
- figure;
- plot(w,unwrap(angle(H)));
- axis([0 pi -35 5]);grid;
- xlabel('Frequency \omega [rad]');
- ylabel('\theta [rad]');
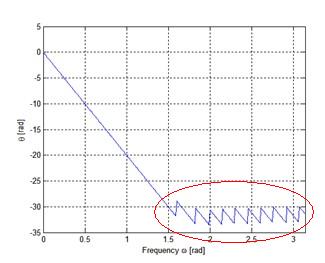
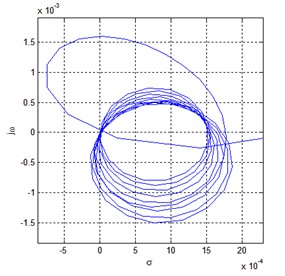
即便是到此，我们解卷绕之后，还是有一个问题，红色的部分，还是在震荡。为什么会有这个震荡呢？
2.为什么要解卷绕之后，相位特性还不是完美的直线？
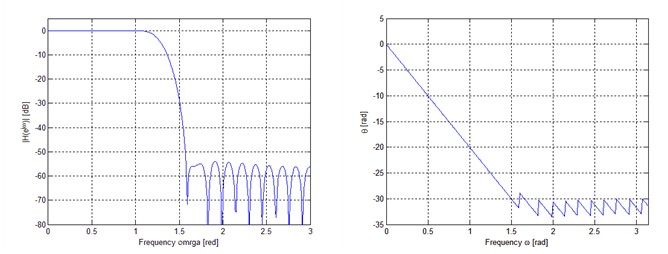
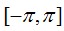，所以，这里产生的跳动是π，而不是2π！我们再将其标注在图上，便于理解。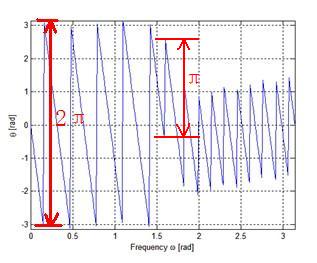 
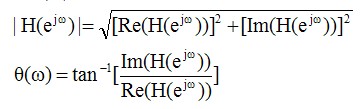
这篇关于相位特性解卷绕的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！
