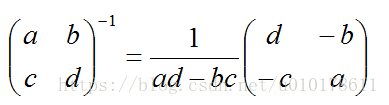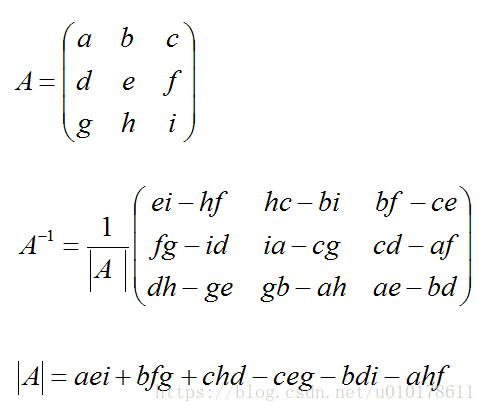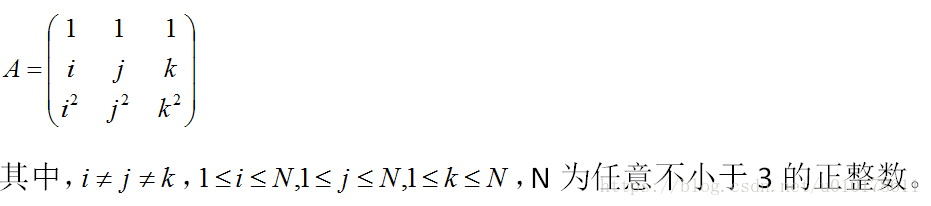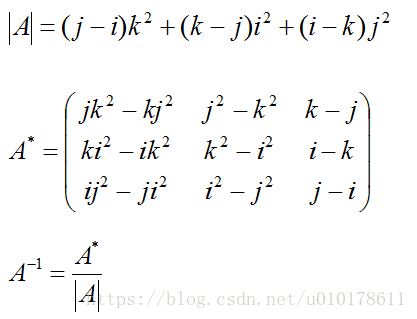本文主要是介绍FEC算法——附录，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！
上篇博文详细介绍了1-3阶冗余的原理，里面涉及到一些二阶三阶矩阵求逆公式和伽罗华域(gf())运算，本文以附录的形式给出来，以供参考。
附录1. 伽罗华域(gf(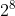
))运算规则
加减法规则
加法和减法操作对应于异或操作：
a + b => a xor b
例如，66+67=>66^67=1
乘法规则
乘法操作运算规则：两个操作数的伽罗华域指数值相加后取255的模值，然后根据计算后所得的新指数查映射表可得最终的结果值。
例如，计算66*67：
1）查附录二的指数表gfByteExpTable[ ]可得66和67对应的指数值为
gfByteExpTable[66]=220、gfByteExpTable[67]=217
2）计算新指数=(220+217)Mod(255)=182
3）查附录二的指数和数据映射表expToValTable[]可得
expToValTable[182]=204
因此，66*67在伽罗华域（gf()）的运算结果为204。
例如，计算66*179
1）查附录二的指数表gfByteExpTable[]可得66和179对应的指数值为
gfByteExpTable[66]=220、gfByteExpTable[179]=252
2）两个指数相加得新指数（mod加）为：(220+179)Mod(255)=217
3）查附录二的指数和数据映射表expToValTable[ ]可得
expToValTable[217]=67
因此，66*179在伽罗华域（gf()）的运算结果为67
除法规则
除法操作运算规则：两个操作数的伽罗华域指数相减（模相减），然后根据计算后所得的新指数查映射表最终的结果值。
例如，计算66/67：
1）查附录二的指数表gfByteExpTable[]可得66和67对应的指数值为
gfByteExpTable[66]=220、gfByteExpTable[67]=217
2）两个指数相减得新指数为：220-217=3
3）查附录二的指数和数据映射表expToValTable[]可得
expToValTable[3]=8
因此，66/67在伽罗华域（gf()）的运算结果为8
例如，计算67/66:
1）查附录二的指数表gfByteExpTable[]可得66和67对应的指数值为
gfByteExpTable[66]=220、gfByteExpTable[67]=217
2）两个指数相减得新指数为：(217-220)+255=-3+255=252
3）查附录二的指数和数据映射表expToValTable[]可得
expToValTable[252]=179
因此，67/66在伽罗华域（gf()）的运算结果为179。
附录2. 伽罗华域（gf(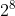)）表
/*****************************************************************
整个GF(2^8)的所有符号的数值表示列表出来，结果如下：
******************************************************************/
unsigned char expToValTable[256]=
{ 1, 2, 4, 8, 16, 32, 64, 128, 45, 90, 180, 69, 138, 57, 114, 228,
229, 231, 227, 235, 251, 219, 155, 27, 54, 108, 216, 157, 23, 46, 92, 184,
93, 186, 89, 178, 73, 146, 9, 18, 36, 72, 144, 13, 26, 52, 104, 208,
141, 55, 110, 220, 149, 7, 14, 28, 56, 112, 224, 237, 247, 195, 171, 123,
246, 193, 175, 115, 230, 225, 239, 243, 203, 187, 91, 182, 65, 130, 41, 82,
164, 101, 202, 185, 95, 190, 81, 162, 105, 210, 137, 63, 126, 252, 213, 135,
35, 70, 140, 53, 106, 212, 133, 39, 78, 156, 21, 42, 84, 168, 125, 250,
217, 159, 19, 38, 76, 152, 29, 58, 116, 232, 253, 215, 131, 43, 86, 172,
117, 234, 249, 223, 147, 11, 22, 44, 88, 176, 77, 154, 25, 50, 100, 200,
189, 87, 174, 113, 226, 233, 255, 211, 139, 59, 118, 236, 245, 199, 163, 107,
214, 129, 47, 94, 188, 85, 170, 121, 242, 201, 191, 83, 166, 97, 194, 169,
127, 254, 209, 143, 51, 102, 204, 181, 71, 142, 49, 98, 196, 165, 103, 206,
177, 79, 158, 17, 34, 68, 136, 61, 122, 244, 197, 167, 99, 198, 161, 111,
222, 145, 15, 30, 60, 120, 240, 205, 183, 67, 134, 33, 66, 132, 37, 74,
148, 5, 10, 20, 40, 80, 160, 109, 218, 153, 31, 62, 124, 248, 221, 151,
3, 6, 12, 24, 48, 96, 192, 173, 119, 238, 241, 207, 179, 75, 150, 0 };
/***************************************************************
整个伽罗华域GF(2^8)的符号指数表
*****************************************************************/
unsigned char gfByteExpTable[256] =
{ 255, 0, 1, 240, 2, 225, 241, 53, 3, 38, 226, 133, 242, 43, 54, 210,
4, 195, 39, 114, 227, 106, 134, 28, 243, 140, 44, 23, 55, 118, 211, 234,
5, 219, 196, 96, 40, 222, 115, 103, 228, 78, 107, 125, 135, 8, 29, 162,
244, 186, 141, 180, 45, 99, 24, 49, 56, 13, 119, 153, 212, 199, 235, 91,
6, 76, 220, 217, 197, 11, 97, 184, 41, 36, 223, 253, 116, 138, 104, 193,
229, 86, 79, 171, 108, 165, 126, 145, 136, 34, 9, 74, 30, 32, 163, 84,
245, 173, 187, 204, 142, 81, 181, 190, 46, 88, 100, 159, 25, 231, 50, 207,
57, 147, 14, 67, 120, 128, 154, 248, 213, 167, 200, 63, 236, 110, 92, 176,
7, 161, 77, 124, 221, 102, 218, 95, 198, 90, 12, 152, 98, 48, 185, 179,
42, 209, 37, 132, 224, 52, 254, 239, 117, 233, 139, 22, 105, 27, 194, 113,
230, 206, 87, 158, 80, 189, 172, 203, 109, 175, 166, 62, 127, 247, 146, 66,
137, 192, 35, 252, 10, 183, 75, 216, 31, 83, 33, 73, 164, 144, 85, 170,
246, 65, 174, 61, 188, 202, 205, 157, 143, 169, 82, 72, 182, 215, 191, 251,
47, 178, 89, 151, 101, 94, 160, 123, 26, 112, 232, 21, 51, 238, 208, 131,
58, 69, 148, 18, 15, 16, 68, 17, 121, 149, 129, 19, 155, 59, 249, 70,
214, 250, 168, 71, 201, 156, 64, 60, 237, 130, 111, 20, 93, 122, 177, 150 };
/******************************************************************
*伽罗华域乘法代码: 计算 v1*v2
********************************************************************/
unsigned char gfm(unsigned char v1,unsigned char v2)
{
unsigned char rslt;
unsigned char index;
if(v1==0||v2==0){return 0;}
//指数求和
index = (gfByteExpTable [v1]+ gfByteExpTable [v2])%255;
//查表获取结果
rslt = expToValTable [index];
return rslt;
}
/******************************************************************
*伽罗华域除法代码: 计算 v1/v2
********************************************************************/
unsigned char gfd(unsigned char v1,unsigned char v2)
{
unsigned char rslt;
unsigned char index;
if(v1==0){return 0;}
//指数相减
if(expOf[v1]>=expOf[v2]){
index = gfByteExpTable [v1]- gfByteExpTable [v2];
}else{
index = 255+ gfByteExpTable [v1]- gfByteExpTable [v2];
}
//查表获取结果
rslt = expToValTable [index];
return rslt;
}
附录3. 二阶矩阵求逆公式
如果a=b=1，c=i，d=j，i和j为任意两不相等的整数，则
附录4. 三阶矩阵求逆公式
假设A为如下特殊矩阵：
则，
这篇关于FEC算法——附录的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！
