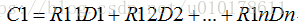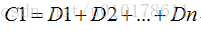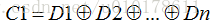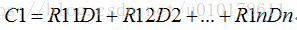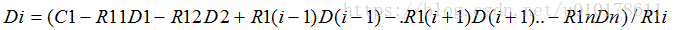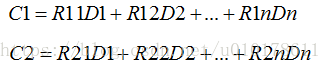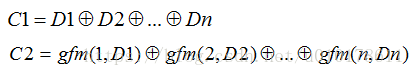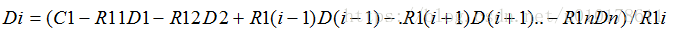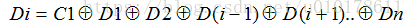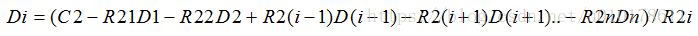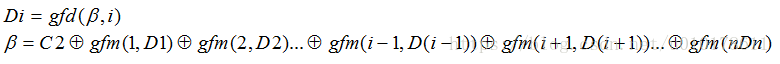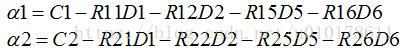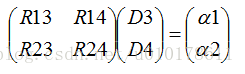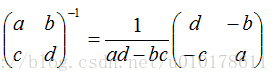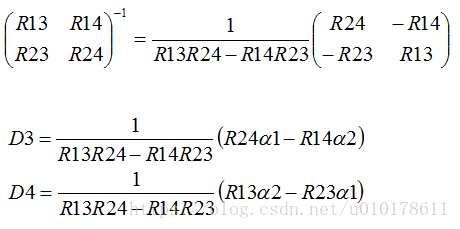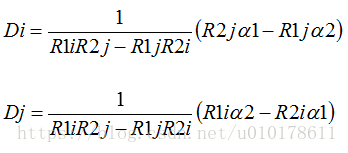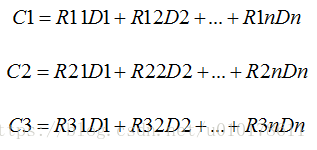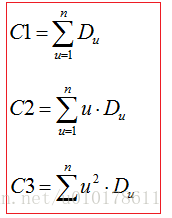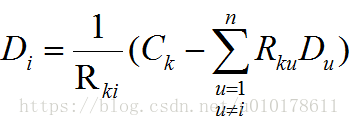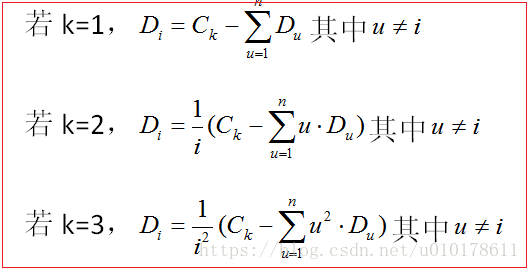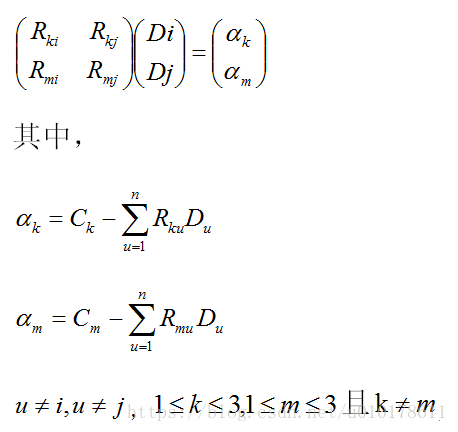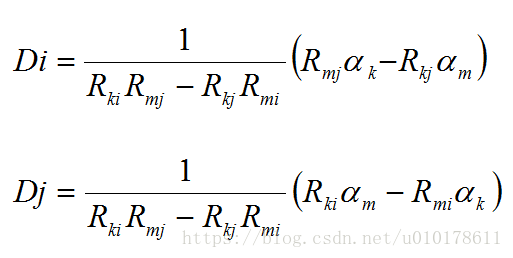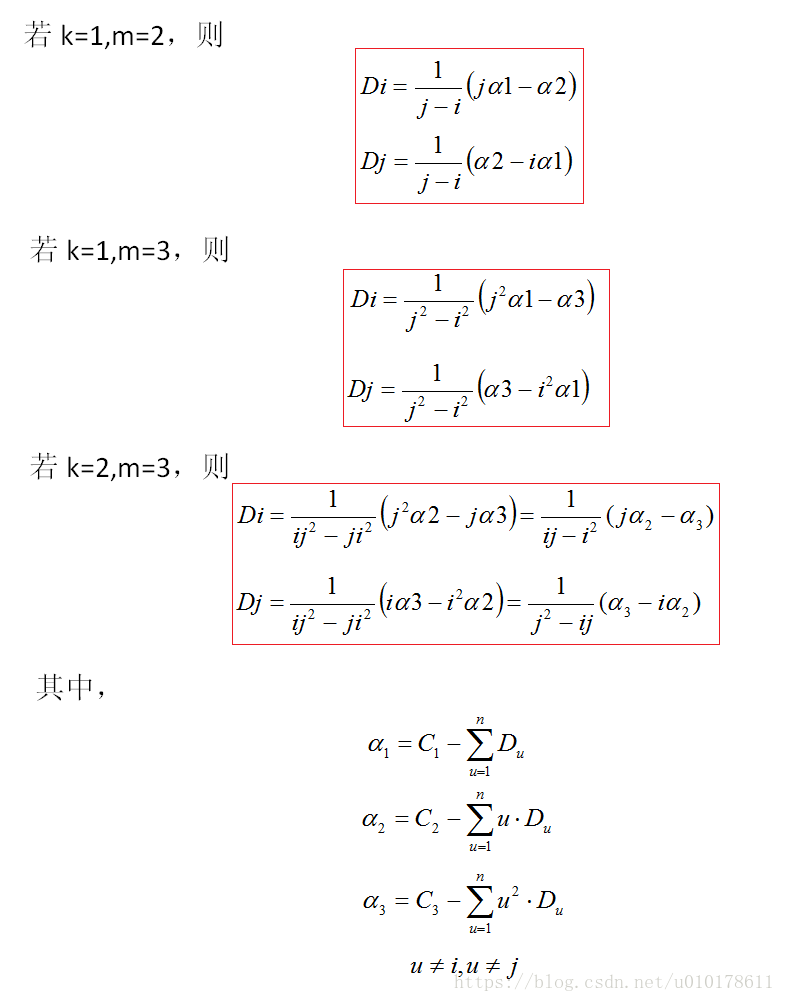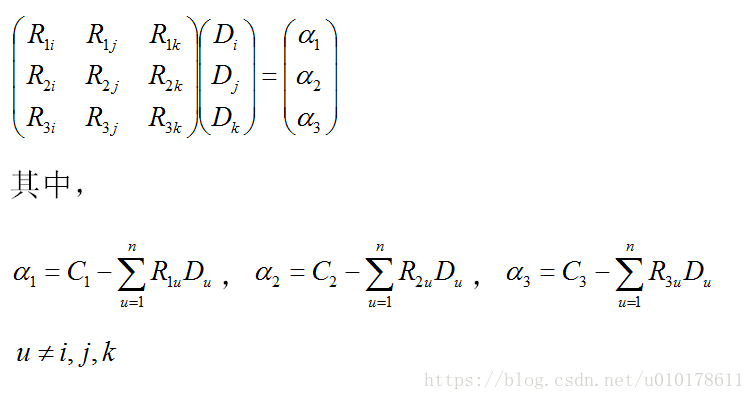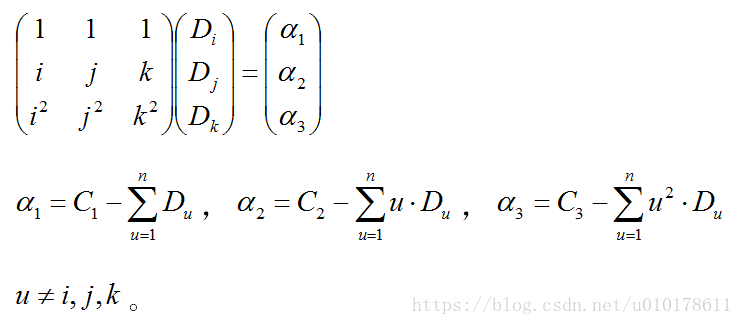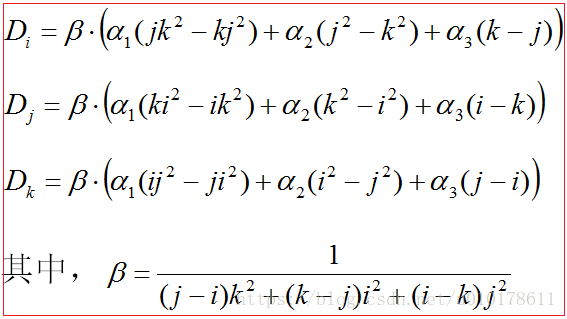本文主要是介绍FEC算法,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
基于IP的语音和视频通话业务为了实时性,一般都是采用UDP进行传输,基站无线一般配置UM模式的RLC承载,因此丢包是不可避免的,在小区信号的边沿则丢包率会更高;为了通话的实时性,一般不会采用接收端发现丢包了然后通知发送端重传的机制,因为这个在应用层的丢包检测和通知发送端重传是非常耗时的。引入前向纠错(FEC)机制是解决实时通话业务丢包的一个很好的机制,FEC的原理就是在发送端发送数据包时插入冗余包,这样即使接收端收到的数据有所丢包(丢包数不大于冗余包时)也是能还原出所有的数据包的。本文介绍FEC算法的原理,只涉及三阶冗余,因为只有前三阶的矩阵运算比较简单,而且实际中也足以够用了,而且阶数越高则传输冗余包占用带宽太大,那就没有意义了,本人曾负责的一个音视频实时通话软件就是只用到三阶冗余,效果已经很好了。
本文对FEC算法进行一步一步的数学推导,让不了解FEC的读者看完后可以有很好的理解,从而可以使用本文的FEC算法到实际项目中,或者为项目设计出更好的FEC算法;同时也重温一下大学的线性代数吧。
- 零阶冗余(没有冗余)
没有加入冗余数据,直接原始数据发送,假设原始数据为D1、D2、D3、...、Dn,则发送的数据就是D1、D2、D3、...、Dn。

- 一阶冗余
所谓一阶冗余算法,就是每n个数据插入一个冗余数据(也即FEC编码组长度为n+1);这n个数据和其对应的冗余数据构成一组数据,这组数据中丢掉任何一个数据都可以通过另外n个数据恢复出来。
发送端编码

如上图示,左边矩阵为编码矩阵,就是在单位矩阵下面插入一行冗余算法参数,右边的C1为计算出来的冗余数据。
令R1i=1,i=1,2,...,n,则上式子可以简化为:
采用伽罗华有限域(Galois field :)运算,则可将加减法运算化为异或运算,因此C1的计算公式简化为:
接收端解码
如果接收端收到的某组数据丢失了一个,则可以通过如下公式推导出恢复丢失数据的公式;下图我们假设丢失的数据为D2,则D2的恢复矩阵运算为:
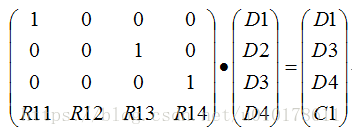
可得,
因此可得到D2的恢复公式:
一般地,若丢失的数据为Di,其中i=1,2,...,n,Di的恢复公式为:
令R1i=1,且采用伽罗华有限域运算,则上式子可以简化为:
- 二阶冗余
就是每n个数据插入两个冗余数据(也即FEC编码组长度为n+2);这n个数据和其对应的冗余数据构成一组数据,这组数据中丢掉任何一或两个数据都可以恢复出来。
发送端

上式左边的矩阵成为编码矩阵,右边的C1、C2为冗余数据,其中:
令R1i=1、R2i=i,其中i=1,2,...,n,且采用伽罗华有限域运算,则上式子可以简化为:
其中gfm()函数表示伽罗华域乘法运算,gfm(i,Di)表示i和Di在伽罗华域的乘法运算。
接收端
场景1、丢失一个数据包Di,冗余包C1没有丢失,则可以通过接收到的数据包和冗余数据C1恢复出Di,其恢复算法和一阶冗余算法的一样:
令R1i=1,i=1,2,...,n,且采用伽罗华有限域运算,则上式子可以简化为:
场景2、丢失一个数据包Di,冗余包C1也丢失,C2没有丢失,则可以通过接收到的数据包和C2恢复出Di,其恢复算法推导如下:
令R2j=j,则上式可以简化为:
若采用伽罗华域运算,则上式可以简化为:
其中gfm()函数表示伽罗华域乘法运算,gfm(i,Di)表示在伽罗华域的乘法运算i*Di,gfd()函数表示伽罗华域除法运算,gfd(a,b)表示在伽罗华域的除法运算a/b。
场景3、丢失两个数据包Di、Dj,冗余包C1和C2没有丢失,则可以通过接收到的数据和冗余数据C1、C2恢复出Di和Dj,其恢复公式推导如下:

整理后为:

经过行操作消元整理后为:
其中,
因此,求解D3、D4本质就是解如下方程:
上式两边乘以矩阵的逆就可以求解出D3、D4:
再结合根据二阶方阵的求逆公式:
可以求解出:
一般地,如果传输中丢失Di和Dj数据包,则Di和Dj的求解公式为:
令R1i=1、R2j=j,i=1,2,..., j=1,2,...,可以简化为:
采用伽罗华域运算,则上面的式子变为:
- 三阶冗余
所谓三阶冗余,就是每n个数据插入三个冗余数据;这n个数据和其对应的冗余数据构成一组数据,这组数据中丢掉任意m个(m<=3)数据都可以通过收到的其它数据恢复出来。
发送端
上式左边的矩阵成为编码矩阵,右边的C1,C2,C3为冗余数据,其中:
令R1j=1、R2j=j、R3j=j^2,其中j=1,2,...,n,则:
采用伽罗华域(gf())运算,可以将加减法变为异或操作,乘除法变为加减法的查表操作;C1就是一阶冗余数据,C2就是二阶冗余数据,C3就是三阶冗余数据。
接收端
场景1,仅丢掉一个数据包Di,接收到一个冗余包Ck,则恢复Di的公式为:
其中,k = 1 或 2 或 3 ,u ≠ i。
令R1u = 1、R2u = u、R3u = u^2,则:
场景2,丢掉两个数据包Di、Dj,接收到两个冗余包Ck、Cm;经过推导可以化简为解如下二元线性方程组:
解方程可得:
若令R1j=1、R2j=j、R3j=j^2,其中j=1,2,...,n,则上式Di和Dj的求解可简化为:
场景3,丢失三个数据包Di、Dj、Dk,且接收到三个冗余包C1、C2、C3,则经过简单的推导将丢失数据包的恢复计算抽象为解如下三元线性方程组:
若令R1j=1、R2j=j、R3j=j^2,其中j=1,2,...,n,则上式Di和Dj的求解可简化为:
根据附录的三阶矩阵求逆公式,就可以直接求解出Di、Dj、Dk:
采用伽罗华域(gf())运算,可以将加减法变为异或操作,乘除法变为加减法的查表操作。
注:
【1】FEC的编码和解码都是使用伽罗华域(gf())运算。
【2】文中使用的冗余矩阵是范德蒙特行列式,这样构建出来的冗余矩阵,最后接收端解码求矩阵的逆时,不会遇到奇异矩阵的场景,否则如果出现奇迹矩阵则接收端就无法求解出丢失的数据包了。
【3】 相关的伽罗华域(gf())运算和矩阵运算请参考《FEC算法——附录》
这篇关于FEC算法的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!